Abstract
Hydrides of actinides, their magnetic, electronic, transport, and thermodynamic properties are discussed within a general framework of H impact on bonding, characterized by volume expansion, affecting mainly the 5f states, and a charge transfer towards H, which influences mostly the 6d and 7s states. These general mechanisms have diverse impact on individual actinides, depending on the degree of localization of their 5f states. Hydrogenation of uranium yields UH2 and UH3, binary hydrides that are strongly magnetic due to the 5f band narrowing and reduction of the 5f-6d hybridization. Pu hydrides become magnetic as well, mainly as a result of the stabilization of the magnetic 5f5 state and elimination of the admixture of the non-magnetic 5f6 component. Ab-initio computational analyses, which for example suggest that the ferromagnetism of β-UH3 is rather intricate involving two non-collinear sublattices, are corroborated by spectroscopic studies of sputter-deposited thin films, yielding a clean surface and offering a variability of compositions. It is found that valence-band photoelectron spectra cannot be compared directly with the 5f n ground-state density of states. Being affected by electron correlations in the excited final states, they rather reflect the atomic 5f n−1 multiplets. Similar tendencies can be identified also in hydrides of binary and ternary intermetallic compounds. H absorption can be used as a tool for fine tuning of electronic structure around a quantum critical point. A new direction is represented by actinide polyhydrides with a potential for high-temperature superconductivity.
Export citation and abstract BibTeX RIS
1. Introduction
A specific role which actinides play in condensed matter physics and chemistry is related to the 5f electronic states. In elemental light actinide metals (Th-Np), the 5f electrons reside in delocalized states involved in metallic bonding. In the condition of a relatively low density of states at the Fermi level, N(EF), modest electron–electron correlations do not give rise to any atomic magnetic moments and the Pauli paramagnetism is a typical characteristic of the ground state, which can be normal or superconducting. This changes with increasing occupancy of the 5f states and the elements from Am onwards have the 5f states non-bonding and localized in analogy to the 4f states in lanthanides. As elemental Pu is located at the crossover, it means that neither of the two well understood limits, the localized and itinerant, is capturing its essential electronic properties. None of its numerous phases is magnetic, but the paramagnetism is a result of a complex many-body state, which involves both the magnetic 5f5 and non-magnetic 5f6 configuration.
In alloys and intermetallic compounds of light actinides, the band states can be naturally tuned by variations of the crystal structure or by presence of ligand atoms. In the zoo of diverse structures, elements, and stoichiometries, the inter-atomic separation of actinide atoms was identified as a prominent factor, deciding whether a given compound will have a tendency to magnetic order or superconductivity [1]. In case of enhanced inter-actinide distances, a narrowing of the 5f band can eventually give N(EF) large enough to fulfill the Stoner criterion U N(EF) > 1 (where U is the Coulomb repulsion), leading to the onset of magnetic order, appearing as unequal population of states with different spin direction. This can be taken as a first step on a tour towards the 5f localization, which can lead an observer along different pathways, entering exotic emergent phases and watching unprecedented phenomena, as e.g. unconventional superconductivity induced by very strong magnetic fields. Neither previous experience with anomalous 4f systems nor computations within the density functional formalism are reliable guides in this landscape. Nothing like well-defined Kondo effect or valence fluctuation regime can be reliably identified, and permanent ongoing discussions about decades old puzzles (as the nature of hidden order in URu2Si2 [2]) do not help in understanding the underlying logic, when we observe the field of actinides through a viewfinder of different experimental techniques, each related to a particular timescale.
Looking at the 5f magnetism, some unifying elements can be found despite the diversity given by large differences in the 5f (de)localization. The ubiquitous phenomenon is very strong spin-orbit interaction, coupling the spin system with the crystal lattice. Unlike the crystal electric field (CEF) effects in rare earths, the electronic sub-system is so intimately connected with directions of magnetic moment that any reorientation has a dramatic impact on conduction electrons, giving rise to giant magnetoresistance and other spintronics-relevant phenomena. The temperatures of magnetic order are relatively low, typically below the room temperature, unless they are supported by large concentrations of 3d components. Structure and composition changes as well as external variables (pressure, magnetic field) can tune magnetic properties over a large extent. The U–U spacing giving the 5f–5f overlap and the hybridization with non-f states are key parameters. The hydrides belong to compounds which suggest that polar character of bonding may be important not only in ionic compounds as oxides, but also in certain systems with metallic or semi-metallic character. The concept of polar bonding is naturally nothing new, but its workings in systems with conduction electrons is reduced due to long-range Coulomb screening, and the majority of recent theoretical works in actinide hydrides did not analyze its impact on the background of prominent band effects, which are related to inter-atomic spacing.
Besides the fundamental aspects, there are also important practical aspects of actinide (mainly uranium) hydrides, which have certainly a good potential in the field of hydrogen (deuterium, tritium) storage. Although the high atomic mass excludes any mobile applications, stationary applications can benefit from a high volumetric density (≈130 g cm−3), moderate prices of depleted uranium, and particularly from very high difference (seven orders of magnitude) in equilibrium pressure of H2 on U, as low as 10−2 Pa at room temperature and 105 Pa at 700 K. U metal hence works as a getter, capturing valuable tritium in nuclear fusion devices at room temperature, and releasing it again at moderate temperatures [3]. The robustness of the H absorption in U even in the presence of oxygen can be used for hydrogen purification [4]. Uranium hydride can be a component of nuclear fuel for light-water reactors [5] and even thorium hydride is considered for advanced burner reactors [6]. On the other hand, extended studies of details of reaction of H with U and Pu have been undertaken due to hazards brought by corrosion [7, 8].
Despite the significant effort in several fields, there is still a need for a more synthetic description of properties of actinides in elemental and compound form being affected by hydrogen. The present work focuses on this topic with the aim to review, in a single conceptual framework, the electronic and lattice properties of binary and multinary hydrides on the basis of actinides, exploring the particular role of the 5f electronic states.
2. Uranium hydrides in a historical perspective—structure and magnetic properties
Uranium hydrides were systematically studied from 1940's, when the keen reaction of U metal with hydrogen gas was investigated as a function of temperature [9]. The reaction product, which was a fine pyrophoric powder, was, however, difficult to study. Following years of intense research in Poland conducted by the group of W. Trzebiatowski (summarized in retrospection in [10]) revealed that UH3 exhibits ferromagnetism with the Curie temperature TC ≈ 170 K and spontaneous magnetization about 1 μB per formula unit. That was the first indication that the 5f states can lead to magnetic ordering. Very similar properties were found for analogous deuteride. The stable hydride, now labeled as β-UH3, was found to form in a large cubic unit cell, containing 8 U and 32 H atoms. The structure details including H (D) positions were revealed in 1951 by Rundle [11]. Several years later the metastable variant, α-UH3, appeared as a result of hydrogenation of U metal at low temperatures [12]. It has the U-sublattice of bcc type, corresponding to the γ-U phase, which is stable at high temperatures, but with the volume expanded by ≈ 60%. As it was never synthesized as a pure phase, its ferromagnetism with TC very similar to that of β-UH3 was sometimes attributed to the β-phase contamination [13]. However, as we see later, such conclusion was not correct and both UH3 phases have at least magnetic properties very similar to each other.
The high stability of UH3 is most likely the reason why no UH2 phase with the CaF2 structure type (U sublattice forming the fcc structure), known to form for all 4f and most of 5f elements, appears in the equilibrium U–H phase diagram [14]. This phase was synthesized only in a thin-film form by reactive sputter deposition, which generally helps to avoid constraints of thermodynamic equilibrium [15]. UH2 is also ferromagnetic, with TC ≈ 120 K being somewhat lower compared to both UH3 phases.
A comparison of the crystal structures mentioned, shown in figures 1(a), (b) and (c), reveals that despite the U–U coordination being very different in all three phases, the U–H coordination has some similarities. The most striking is location of each H atom into the U4 tetrahedra, which are very similar as to the size, and in which the U–H distances are always 232 pm. As it was pointed out already by Rundle in 1951 [11], this distance is very large if we consider the U metallic radius 156 pm for U and covalent radius 37 pm for H or D [16]. Reading '...the deuterium atoms are found in holes that are far larger than they would seem to require. Since a very great expansion of uranium takes place upon forming the hydride, one cannot attribute the long U–D bonds to the filling of pre-existing holes which happen to be too large. The holes for hydrogen are created by formation of the hydride. Neither can be argued that the long U–D bonds mean a weak uranium-hydrogen interaction...It appears that something else is required before metal-hydrogen distances in heavy metal hydrides are well understood.' [11]. After years, it became evident that the size of H atoms, having only one electron in a charge-neutral state, are very sensitive to an electron transfer from less electronegative ligands. The size can exceed 100 pm when approaching the H− limit e.g. in Fe-based superconductors [17]. The oversize U4 tetrahedra are therefore a fingerprint of a charge transfer towards H, which, as we see later, affects all the fundamental properties of actinide hydrides.
Figure 1. Perspective view of the crystal structures of binary U hydrides with indicated U4 tetrahedra containing the H positions. In β-UH3 (b) the two U sites are distinguished by different hue of green. The 2a positions are dark, 6c positions are light.
Download figure:
Standard image High-resolution imageThe fact that both α- and β-UH3 structures consist of very similar U4-H blocks (the tetrahedra are only somewhat distorted in the β-phase), and which fill the whole space, explains the very similar x-ray density (being 11.12 g cm−3 in α-UH3 and 10.92 g cm−3 in β-UH3). For UH2, in which the space is not filled entirely, the density is lower (10.41 g cm−3). Despite the prominent stability of the uranium trihydrides, there are possibilities to modify their composition by alloying. It was first realized by hydrogen reaction with U6Co, giving a hydride with the β-UH3 structure, denoted as U6CoH18 with TC = 185 K [18]. A similar situation was found for U6Fe, giving the hydride denoted as U6FeH17. It became evident that Fe substitutes U in the β-UH3 structure [19]. A more versatile way to modify the composition is to start from U alloys. The hydrogen absorption, which has to be performed at room temperature to prevent decomposition of the metastable alloys, takes a longer time and requires higher H2 pressures. The products are also more stable in air. The structure is based on β-UH3 in most of cases, and differs by a grain size, which can be as small as 2–3 nm for Mo alloying, while some, such as V doped, exhibit a regular crystallinity. Conventional x-ray diffraction yields only very broad peaks for such very small grain sizes, and the amount of information obtained remains therefore limited. More insight into the structure details was obtained by the PDF analysis [20]. So far, only the Zr alloying gives the α-UH3 structure, which may link to the larger atomic radius of Zr compared to U, while other transition metals used have all the atomic diameters smaller [21].
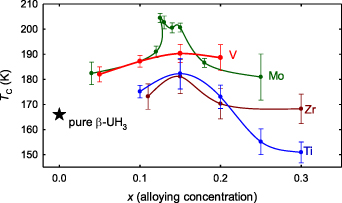
None of the structure details seem to affect magnetic properties. Similar to very small differences between α- and β-UH3, the perturbed crystallinity on the mesoscopic scale has no apparent effect on TC, which at the beginning universally increases with the alloying concentration and reaches maximum in the range 12–15 at.%. The size of the increase does, however, depend on the alloying element (see figure 2). The largest was found for Mo, where TC exceeds 200 K [21, 22]. The influence of Mo, which is unlikely to contribute by sizeable own magnetic moments, is arguably only indirect, modulating the H/U ratio, when one U atom of the U4 tetrahedra is replaced by Mo. Replacing two U atoms by Mo already makes the H position unstable, so the H/U ratio tends to decrease above certain Mo concentration. The very small grain size of alloyed hydrides may not be reflecting any fundamental characteristics. A tentative reason can be found in very slow grain growth, perhaps due to Mo blocking the diffusion of hydrogen. The grain size of hydrides is a result of interplay of incubation and grain growth. Fast grain growth following a slow incubation of hydride gives large grains. If we neglect the effect of inclusions, H2 molecules have to dissociate on the top of UO2 coating, diffuse through the UO2 overlayer, and only then the volume expansion exposes fresh U/UH3 surface to further hydrogenation, depending on diffusion. If due to any reason the incubation becomes faster than the grain growth, the grain size decreases. In general, one can think also about other reasons, as local distortions of structure by Mo prevent a long-range coherence.
Figure 2. Summary of variations of TC values in (UH3)1-x Tx systems. For higher concentrations of alloying elements the systems become inhomogeneous even if the single-phase character is preserved. Notice that the plot contains both hydrides with the α-UH3 (Zr) and β-UH3 (Mo, V, Ti) structures. Reprinted from [22], Copyright (2021), with permission from Elsevier.
Download figure:
Standard image High-resolution imageThe apparent irrelevance of crystal structure and presence or absence of 3D periodicity is contradictory to common U-based systems, e.g. intermetallics, the properties of which can be dramatically different for allotropic modifications of one compound or for reduced crystallinity, which typically reduces magnetic ordering temperatures [23, 24].
The improved stability of alloyed UH3 while maintaining the strong ferromagnetism brought an opportunity of high-pressure study using conventional techniques. In [25] pressures exceeding 3 GPa were applied on (UH3)0.82Mo0.18. It was found that the TC value decreases with pressure at a rate dTC/dp = −2.05 K GPa−1, which gives the relative change with respect to volume dlnTC/dlnV = 1.1, which is a similar value like in US, indicating an intermediate 5f delocalization.
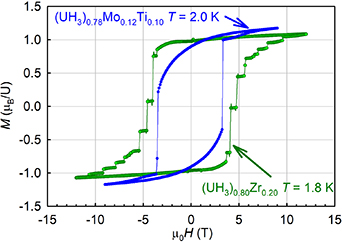
Very wide hysteresis loops (reaching almost 10 T width—see figure 3) are one of the striking features of U hydrides. The general reason is in high magnetic anisotropy, related to large orbital moments, linking the moments orientation with a particular crystallographic direction. Despite quite general magnetization of 1.0–1.3 μB per U atom, one can see a difference in saturation behavior. The β-UH3 type hydrides saturate more gradually, which can be related to a non-collinearity of the two U sublattices (see below), as well as to nanocrystallinity of the alloyed hydrides. The magnetizations can be compared with the size of U moments in β-UD3, obtained by neutron diffraction as (1.45 ± 0.11) μB. The moments at 2a and 6c U sites were assumed as collinear and their size came out the same [26].
Figure 3. Examples of wide hysteresis loops of alloyed U hydrides. The shape is different for α-UH3 type, (UH3)0.80Zr0.20, and β-UH3 type, (UH3)0.78Mo0.12Ti0.10, the latter showing slower approach to saturation. Reprinted from [27], Copyright (2022), with permission from Elsevier.
Download figure:
Standard image High-resolution image3. Other actinides
Interestingly, the trihydrides with crystal structures analogous to α- and β-UH3 were observed also for Pa. The lattice parameters a = 415.0 pm for α-PaH3 and 664.8 pm for β-PaH3 are practically identical to the isostructural uranium hydrides [28], implying that the Pa-H distances are very close to 232 pm as found in UH3.
Entirely different pattern was found for Th. There is no trihydride, the higher hydride forms in the Th4H15 stoichiometry (i.e. ThH3.75), crystallizing in a unique large cubic structure type, described by Zachariasen [29], and later somewhat corrected by neutron diffraction on Th4D15. Two different H positions give the Th-H(D) distances 246 pm and 227–238 pm, respectively, for Th-HI and Th-HII [30].
Hydrides of transuranium actinides follow a different and more regular pattern, known from lanthanides, exhibiting a sequence of fcc dihydrides, which can accommodate a substantial off-stoichiometry mainly towards the higher H concentrations, AnH2+x , and they are followed by trihydrides. It is interesting that for lanthanides the progress from dihydrides to trihydrides leads to a loss of metallic behavior, giving rise to the spectacular switchable mirror effect [31]. UH3 is, as we see below, metallic (or at least semi-metallic), which indicates that the 5f states are not localized as 4f states in lanthanides and their involvement in metallic bonds yields a 5f band at the Fermi energy.
The reaction of plutonium with hydrogen has been a convenient route to prepare plutonium powder since the Manhattan project. It turned out that the cubic fcc type exists for PuHx in the concentration range x = 1.9–2.7. In ideal PuH2, H atoms occupy Pu4 tetrahedra, with the Pu-H distance 231 pm (for details see [32] and references therein). For higher H occupancies, additional H positions with octahedral coordination are gradually occupied and the lattice parameter slightly decreases [33, 34]. This trend of volume reduction was reproduced in electronic-structure calculations [35, 36] which revealed that the ionic charges of the H atoms decrease with increasing hydrogen concentration, making their ionic radii smaller and thus allowing for a smaller lattice parameter. For H concentrations close to x = 3, either hexagonal LaF3 structure or orthorhombic YF3 were detected [37]. All Pu hydrides were found magnetic. PuH2 is antiferromagnet with TN = 30 K. PuH2+x (still in the CaF2 structure type) becomes ferromagnetic with gradually increasing Curie temperature. The Pu moments determined by neutron diffraction of Pu deuterides are similar irrespective of the x values, yielding (0.8 ± 0.2) μB per formula unit [26]. The fcc hydrides are essentially metallic, with ρ = 70 μΩcm at T = 4 K for PuH1.93. The values seem to increase and a negative dρ/dT develops for higher x [38]. PuH3 is ferromagnet with TC = 101 K [39]. Magnetometry became therefore a convenient tool for detection of traces of H in U or Pu [40].
The relatively large Pu moments are strongly suggestive of the 5f5 state, different from the non-magnetic state of Pu metal and its compounds with the 5f occupancy exceeding n5f = 5 [41], which are likely in a valence fluctuating regime, involving fluctuations to the non-magnetic 5f6 state [42, 43]. We can assume that in this case (unlike U) the Pu-H bonds reduce the mean 5f occupancies.
Less is known about Np hydrides. Phases similar to Pu hydrides, with extended fcc range of stability and narrow hexagonal range of NpH3, were identified [44]. All NpH2+x systems have a non-magnetic ground state, explained as CEF effect on 5f4 state. This implies the 5f localization due to the Np-H interaction [39].
The similarity of transplutonium elements with rare earths manifests itself by analogous phase relations, with fcc AnH2+x and AnH3, which has a hexagonal structure, some details of which are not known yet. The progressively decreasing lifetime with atomic number Z prevented to collect information on solid-state properties. Their lattice parameters are summarized in table 1.
Table 1. Overview of lattice parameters of actinide fcc dihydrides and hexagonal trihydrides. All data in pm.
| fcc dihydrides | ThH2 | UH2 * | NpH2 | PuH2 | AmH2 | CmH2 | BkH2 |
| a = 548.9 | a = 536.0 | a = 534.3 | a = 535.9 | a = 534.8 | a = 532.2 | a = 523 | |
| [45] | [15] | [46] | [32] | [47] | [48] | [49] | |
| *metastable | |||||||
| Hexagonal trihydrides | Another structure type | Another structure type | NpH3 | PuH3 | AmH3 | CmH3 | BkH3 |
| a = 377.1 | a = 378 | a = 377 | a = 376.9 | a = 645.4 | |||
| c = 671.3 | c = 655 | c = 675 | c = 673.2 | c = 666.3 | |||
| [46] | [32] | [47] | [48] | [49] |
4. Bulk properties—transport
Thorium hydrides, which are metallic, attracted attention mainly because of their superconducting properties. Namely Th4H15, synthesized as monolithic under high pressure and temperature, was found superconducting [50] below ≈8 K. The high critical superconductivity temperature Tc for Th4H15 was explained on the basis of Eliashberg theory in [51], where it was also deduced that the H concentration in ThH2 is insufficient for appreciable Tc value. Indeed, no superconductivity was found down to T = 1.2 K for ThH2 [50]. More detailed study of the superconductivity of Th4H15 and Th4D15 revealed an isotope effect, namely an increase of Tc = 8.28 K in the hydride to 8.48 K in the deuteride [52]. An interesting feature, not very common in superconductors, is enhancement of Tc under pressure, which is initially linear with a slope dTc/dp = 0.42 K GPa−1 and slowly saturating when approaching the experimental pressure limit of 3 GPa [53]. Although absolute values of resistivity are not available, the superconducting ground state means that Th4H15 is metallic. Other evidence is the Sommerfeld coefficient of the electronic specific heat in the normal (non-superconducting) state (8.07 ± 0.14) mJ (mol Th)−1 K−2 for Th4H15 and (7.84 ± 0.25) mJ (mol Th)−1 K−2 for Th4D15 [54]. The values are actually much higher than for Th metal with γ = (4.31 + 0.05) mJ mol−1 K−2 [55], which is also superconducting, but with lower Tc = 1.374 K.
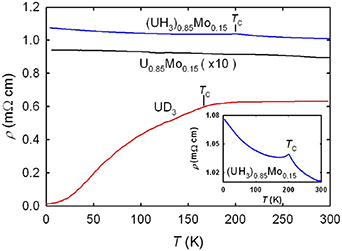
The metallic character of U hydrides is not entirely obvious. Electrical resistivity ρ(T), obtained on a monolithic polycrystalline piece synthesized at high temperatures and very high H2 pressures [56], exhibits a metallic behavior: ρ(T) increases up to the Curie temperature TC, above which it saturates (see figure 4). This makes an impression of dominant standard spin disorder scattering in ferromagnets. The unusual feature is the resistivity value at high temperatures, 600 μΩcm, which exceeds the Mott limit of 200 μΩcm considered as maximum value of metallic resistance, at which the electron mean free path is as low as interatomic distances. This indicates a low concentration of electrons capable to transport charge at the Fermi level. However, the Sommerfeld coefficient γ = 33.9 mJ mol−1 K−2 is markedly enhanced compared to α-U (10.0 mJ mol−1 K−2 [55]). This is only an apparent contradiction. The γ-value, reflecting the density of quasiparticle states and the reaction of the electron system to thermal excitation, does not have to correspond to the 'bare' density of states of the ground state.
Figure 4. Temperature dependence of electrical resistivity ρ(T) of UD3 (from [56]) compared with (UH3)0.85Mo0.15 and its precursor U0.85Mo0.15, which was multiplied by the factor of 10 for easier comparison. The inset shows the detail of the cusp at TC of (UH3)0.85Mo0.15 located at 203 K. Reprinted figure with permission from [57], Copyright (2013) by the American Physical Society.
Download figure:
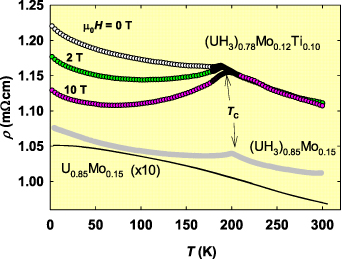
Standard image High-resolution imageThe dramatically modified ρ(T) of alloyed UH3, which is rather flat, reflects the statistical distribution of alloying elements, as e.g. Mo. It actually served as a piece of evidence against clustering of alloying elements. At first glance, it copies ρ(T) of the precursor random bcc alloys (as U0.85Mo0.15 in the case depicted in figure 4). Only the absolute values, being close to 100 μΩcm in the alloys, are by a factor of 10 higher in the hydrides, reaching again the realm of semi-metallicity. A close inspection reveals a small but sharp cusp, coinciding with TC (see the inset). The main difference to pure UH3 is thus in the fact that the magnetically ordered state does not provide the lattice coherence needed for the ρ(T) drop. Surely, the U-Mo randomness remains, but that is not all. The negative dρ/dT follows an almost uninterrupted course from the paramagnetic to ferromagnetic range. However, application of magnetic field of several Tesla, which has no impact in the paramagnetic range, causes a pronounced negative magnetoresistance effect. This points to the effect of static randomness in moments orientation, most likely related to very small grain size of the order of several nm. In conditions of strong magnetocrystalline anisotropy (calculations indicate a prominence of [111] direction, see below), the ordered state is then equivalent to a non-collinear ferromagnetism. Unlike the U moments fluctuating in the paramagnetic state, the ferromagnetic state can be easily affected by magnetic fields, aligning the moments gradually into the field direction against the randomly distributed anisotropy. However, the effect of anisotropy, which gets stronger with decreasing T, eventually dominates at the low temperature end, where the negative dρ/dT reappears even for μ0 H = 10 T (figure 5).
Figure 5. Comparison of electrical resistivities of (UH3)0.85Mo0.15, its precursor U0.85Mo0.15, and (UH3)0.78Mo0.12Ti0.10 (β-UH3 structure type and grain size similar to (UH3)0.85Mo0.15, with TC = 188 K), which was investigated in several magnetic fields (field-cooled mode). The resistivities in the ordered state are very much dependent on magnetic history, reflecting the broad magnetization hysteresis loop. In particular, it was shown that they scale as Δρ ∝ M2. Reprinted figure with permission from [59], Copyright (2017) by the American Physical Society.
Download figure:
Standard image High-resolution imageThe situation, in which the magnetic disorder continues in the static form affecting the resistivity in the same way, gives evidence that the origin of the negative resistivity slope dwells in a weak localization mechanism. It is a quantum interference effect preferring backward scattering of conduction electrons over forward scattering. The temperature dependence is actually given by population of phonons and electron-phonon scattering, weakly inelastic in nature, which leads to a decoherence of quantum states at elevated temperatures [58]. It was suggested that such phenomenon, appearing when the mean free path is comparable with the electron wavelength, is responsible for the negative slope of a broader class of actinide compounds, which could be otherwise labeled as Kondo systems [59].
Interesting comparison is provided by the U-Zr hydrides, which do not exhibit the negative resistivity slope, but only a simple flat ρ(T) above TC [60]. They have a significantly larger grain size, yielding a larger coherence length of the ferromagnetic structure. The negative slope is also absent at the U-Zr precursor alloys [61], probably due to Zr being closer to U in terms of atomic radius as well as electronegativity.
Very similar ρ(T) dependences were observed also for sputter deposited U-Mo hydride films, which offer a larger structure and compositional variability than the bulk hydrides. Depositing on a cooled substrate, one can obtain practically amorphous hydrides, in which the negative slope is even more pronounced. This underlines the link between dρ/dT < 0 and structural disorder [22].
5. Bulk properties—heat capacity
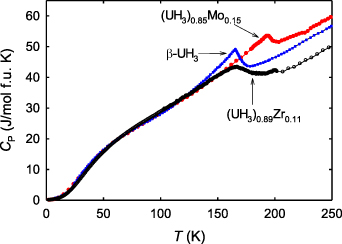
Studies of the heat capacity of pyrophoric hydrides like UH3 are challenging. Excellent data on β-UH3, obtained already in 1959 [62], exhibit a pronounced and sharp magnetic phase transition at 170 K (figure 6). More recent experiments with alloyed UH3, more resistant to oxidation, brought samples suitable for the now common microcalorimetry using the Quantum Design PPMS system. As seen from figure 6, the TC anomaly for U-Zr hydrides (α-UH3 structure) and U-Mo hydrides (β-UH3 structure) are broader and reflect the small increase of TC. Analyses of low-temperature part show that the Sommerfeld coefficient is typically close to 30 mJ mol−1 K−2 in all the cases.
Figure 6. Temperature dependence of heat capacity C(T) for β-UH3 [62] compared with (UH3)0.85Mo0.15 [57] and (UH3)0.89Zr0.11 [60].
Download figure:
Standard image High-resolution imageThe entire shape, displaying a knee in C(T) around 50 K, followed by approximately linear increase, which continues even above TC, indicates a strongly non-Debye like lattice specific heat. An insight is provided by ab-initio computations [63], which reveal low-energy acoustic phonons supplemented by high-energy optical phonons (H vibrations), the latter being populated only at temperatures approaching T = 1000 K. The lattice specific heat, derived from the computed phonons, combined with the electronic heat capacity estimated as γ T, where we take the low-temperature γ = 30 mJ mol−1 K−2, still does not give the full account of the heat capacity in the paramagnetic state. This, however, changes if we assume that γ = 60 mJ mol−1 K−2 in the paramagnetic state (see figure 7). Then the agreement is very good and one can even estimate the magnetic entropy, being close to R ln2. The decrease of γ in the ordered state may be related to an increase of U moments in the ordered state compared to the paramagnetic state as found in ab-initio calculations [60]. It is therefore a fingerprint of the band nature of magnetism.
Figure 7. Temperature dependence of the heat capacity C(T) for (UH3)0.89Zr0.11 shown together with the calculated phonon heat capacity (dashed) [63] combined with the electronic term γT for γ = 30 mJ mol−1 K−2, which is deduced at low temperatures (blue line), and 60 mJ mol−1 K−2 (green line), the latter describing well the paramagnetic range where the magnetic entropy is constant.
Download figure:
Standard image High-resolution image6. Computational studies—toward a comprehensive model of UH3
Historically the first computational investigation of UH3 using the density-functional theory (DFT) was performed by Switendick [64] who discussed the electronic configuration of the uranium atom in the hydride. Unfortunately, his study involved substantial simplifications enforced by computational limitations and as such it does not stand to the present standards. A comprehensive study of UH3 and its formation by hydrogenation of the uranium metal was reported by Taylor and coauthors in their series of papers [65–67]. They evaluated transition barriers along the process starting with the adsorption of hydrogen on the metal surface, continuing with its transport toward bulk and its trapping at defect sites, and ending with a phase transformation from the α uranium saturated with hydrogen to the hydride. Comparing the computed equations of state of α- and β-UH3, they found that the α phase should be energetically favorable under pressure (later calculations estimated that α-UH3 becomes stable at approximately 5 GPa [68, 69]). Taylor et al assumed that the hydride starts forming in hydrogen-rich regions that are under stress, being surrounded by a less hydrated metal, the volume of which is lower, and hence α-UH3 should form first as an intermediate phase before β-UH3 as experimentally observed [12]. Although plausible, it is not entirely clear if this is indeed the correct explanation of α-UH3 being an intermediate phase since in experiments in diamond anvil cells, the amount of the α phase is actually reduced when an α- and β-UH3 mixture is compressed, with α-UH3 eventually disappearing entirely [68].
The calculations of Taylor et al did not include spin–orbit coupling, which represents a fair approximation when it comes to the total energy, equation of state, and related quantities. It does, however, fail substantially in the description of magnetism of the hydrides. The spontaneous magnetization was found to be approximately 2.5 μB per U atom in [67], markedly overestimating the experimental value ≈1 μB. Moreover, the computed magnetization is of purely spin origin. When the spin–orbit coupling is included in the calculations, a large orbital contribution to the magnetization appears and points in the opposite direction than the spin contribution, which is typical for uranium magnetism. In the local density approximation (LDA), the magnitude of the orbital magnetic moment comes out essentially identical as the magnitude of the spin magnetic moment and hence they nearly cancel [60]. In the generalized gradient approximation (GGA), the orbital moment is larger, thus the total magnetization is dominated by the orbital contribution, but its magnitude is still strongly underestimated compared to experimental data.
It is generally accepted that approximations like LDA and GGA often underestimate the correlations among the uranium 5f electrons, which are the electrons that carry the majority of the magnetism, and that a better model for these correlations may be required to improve the description of the magnetism. Such a better model is provided by the DFT + U method [70, 71] that adds orbital-dependent terms, inspired by the Hubbard model, to the exchange-correlation functional. These additional terms enhance the orbital polarization and with it also the orbital contribution to the magnetic moment. Apart from increasing the magnetic moment, the DFT + U method tends to localize the 5f states and reduce their contribution to bonding. Consequently, the Hubbard +U terms typically expand the lattice (see table 2 for illustration). They also enhance an energy gap between occupied and empty 5f states. These features of the DFT + U method put constraints on the additional parameters, namely Coulomb U and Hund J, that enter the DFT + U exchange-correlation functional. It turns out that the lattice parameter estimated by GGA is very close to experiment [25, 66] and hence the U value cannot be large. On the other hand, LDA underestimates the lattice parameter and therefore it needs to be combined with a larger U [72]. The valence-band spectroscopy can discriminate between these two cases: the positions of the occupied and unoccupied 5f states in UH3 are very close to the positions of the 5f states in uranium metal [73]. Since the uranium metal is very well described by DFT without any Hubbard correction, the correction cannot be large in UH3 either, which indicates that GGA + U with a rather small Coulomb U should be the best model for the electronic structure of UH3 among the DFT + U family of methods.
Table 2. Performance of several DFT-based methods in modeling selected lattice properties of the ferromagnetic state of uranium hydrides collected from the literature. The LDA and GGA functionals (PBE and PW91 are variants of GGA) underestimate the lattice parameter a, which can be compensated by adding a Hubbard correction +U to the uranium 5f states. The correction tends to localize the 5f electrons, and hence it reduces their contribution to bonding and expands the lattice. No similarly clear trend can be identified for the elastic constants Cij and bulk modulus B. The best model among the DFT-based methods discussed in the text is indicated in bold.
| Method | SOC | a (pm) | C11 (GPa) | C12 (GPa) | C44 (GPa) | B (GPa) | source | |
|---|---|---|---|---|---|---|---|---|
| UH2 | PBE + U, U= J (0.5 eV) | Yes | 513.5 | 99 | 63 | 45 | 75 | [63] |
| Experiment | 536.0 | [15] | ||||||
| α-UH3 | PW91 | No | 413.0 | 213 | 50 | 48 | 104 | [66] |
| LDA | No | 400.0 | 216 | 57 | 50 | 110 | [72] | |
| LDA + Ueff (4.0 eV) | No | 412.5 | 221 | 63 | 53 | 116 | [72] | |
| PBE + Ueff (0.6 eV) | No | 413.4 | 109 | [74] | ||||
| PBE + U, U= J (0.5 eV) | Yes | 417.0 | 203 | 38 | 64 | 93 | [63] | |
| Experiment | 416.0 | 104 | [68] | |||||
| β-UH3 | PW91 | No | 658.0 | 227 | 102 | 60 | 144 | [66] |
| PBE | Yes | 659.5 | 96 | [25] | ||||
| LDA | No | 638.2 | 201 | 92 | 57 | 128 | [72] | |
| LDA + Ueff (4.0 eV) | No | 662.2 | 222 | 70 | 58 | 120 | [72] | |
| PBE + Ueff (0.6 eV) | No | 661.9 | 102 | [74] | ||||
| PBE + U, U= J (0.5 eV) | Yes | 667.6 | 204 | 34 | 62 | 91 | [25, 63] | |
| Experiment | 664.0 | 97, 116 | [68, 75] |
A simplified variant of GGA + U [76], which does not include the Hund J explicitly but folds it into an effective Coulomb Ueff = U – J, was applied to UH3 by Jun et al [74]. They found that a small Ueff = 0.6 eV accurately reproduces many properties, such as the lattice parameters, energy of formation, or the thermal expansion. The magnetic moments, however, are underestimated analogously to the plain GGA. These results indicate that taking into account Hund J explicitly is at least as important as the Coulomb U, similarly to the so-called Hund's metals [77], the physics of which has been intensively studied in the context of iron-based superconductors. Following this reasoning, we arrive at the most comprehensive DFT + U model for UH3 (and also UH2) formulated so far, which employs GGA, U = 0.5 eV and J = 0.5 eV, and which describes correctly the lattice parameters, elastic properties as well as magnetism, including the Curie temperature [25, 63]. The Hund J= 0.5 eV was calculated from the atomic number Z using the empirical rule J = 0.33 + 0.070(Z−89) [78], the Coulomb U was adjusted to reproduce the experimental lattice constant and magnetic moment of α-UH3, see [63] for details. The setting of the Coulomb repulsion U being equal to the Hund exchange J makes the DFT + U method similar to the orbital-polarization method [79–81]. In the following we compare behavior of dihydrides and trihydrides obtained with this computational model.
From table 2 we see that in the case of UH2 the C12 value is of the order of C11, whereas for α- and β-UH3 much smaller C12 is identified. The elastic anisotropy for a cubic crystal is defined as Az = 2C44/(C11 − C12) [82], where the elastic constant C44 represents an elastic resistance against trigonal (along body diagonal) deformation and C11 − C12 against tetragonal deformation. In the case of Az = 1, the solid behaves as elastically isotropic. For more details and analysis of bonding contributions to both deformations we refer the readers to [83, 84]. It turns out that UH2 and α- and β-UH3 behave elastically opposite to each other, as the Az of UH2 equals 2.5, i.e. the elastic resistance against trigonal deformation is much larger than against tetragonal one, whereas for α- (β-UH3) the Az is 0.78(0.73), i.e. much stronger against tetragonal deformation than the trigonal one. This is a significant difference (one order of magnitude) related to the hydrides stable in bcc and fcc structures, as solids in bcc structure have usually much higher Az than fcc crystals [85].
Concerning the magnetism, here the behavior of actinide hydrides is also related to the number of Wyckoff positions, their nearest neighbor distances, and the type of actinide element and its magnetic state. In [63] it was deduced that UH2 and α-UH3 possess a collinear ferromagnetic ground-state with the magnetization pointing along the [111] direction with the magnetic moment of 0.89 μB/atom and 1.0 μB/atom, respectively. In the case of α-UH3, this is a result of orbital moment of 3.0 μB/atom and spin moment in the opposite direction, i.e. −2.0 μB/atom, being in a very good agreement with measurements [10, 21, 86]. In the case of β-UH3, the uranium atoms occupy two Wyckoff positions, 2a as in the former hydrides, and 6c. Again, at the 2a position the uranium orbital (spin) moments 2.34 μB (−1.9 μB) point along [111], whereas the moments at the 6c positions are slightly larger, 2.91 μB (−2.05 μB), and inclined by ≈10° from the [111] direction toward the direction of the chains formed by the 6c atoms in the faces of the β-UH3 unit cell (see [63] for details). As schematically illustrated in figure 8, the U–U distance is 376 pm, 361 pm, and 373 pm for 2a in UH2, and α- and β-UH3, respectively, still well above the so-called Hill limit ≈350 pm that secures the appearance of the magnetic ordering. At 6c of β-UH3, the U–U distance is only 334 pm, however, leading to non-collinear ferromagnetic order (with lower energy than any of AF ordering types).
Figure 8. Schematic representation of inter-atomic distances in UH3 and in the α-phase of the U metal. The height of the bars indicates the number of neighbors at that particular distance. UI in β-UH3 is the bcc position (Wyckoff position 2a) and UII are the atoms that form linear chains in the faces of the primitive cell (Wyckoff position 6c).
Download figure:
Standard image High-resolution imageInterestingly, the experimental Curie temperatures for α- and β-UH3 are very similar (≈178 K and 175 K, respectively), both higher than the value of TC in UH2 (≈120 K). A reasonable agreement of calculated values of TC was found, using the mapping of the exchange interactions on the Heisenberg model [63]. The decay of the magnetic exchange interactions as functions of distances between uranium atoms is different. The exchange interaction with the next nearest neighbor J2 of UH2 is negligible, whereas in the case of α- and β-UH3 it is still significant. Moreover, if one takes into account the multiplicity (the number of equivalent nearest-neighbor distances in the structure), the J2 in β-UH3 is the leading term corresponding to the magnetic exchange between uranium atoms at 2a and 6c positions with their mutual distance of 370 pm, far above the Hill limit. The 5th nearest neighbor J5 is again between the 2a and 6c uranium atoms and of negative sign, i.e. antiferromagnetic, and still not negligible. These peculiar interactions affect the non-collinearity of the uranium spin moments and are related to the electron transfer as discussed next.
Although there is no exact and unique way how to divide the electronic charge in a molecule or a solid into contributions belonging to the individual constituent atoms, it is still useful to explore the polar character of bonding using some of the available approximate methods of such partitioning. One of them is the topological decomposition developed by R. Bader, in which dividing surfaces are constructed between atoms such that there is a zero flux (zero gradient of the charge density) perpendicular to these surfaces. The dividing surfaces then define atomic volumes and atomic charges [87, 88].
Table 3 lists the Bader volumes and Bader charges for the pure UH2, α- and β-UH3, as well as for Mo-alloyed β-UH3. First of all, the hydrogen gains a negative charge in all cases. For α-UH3 the charges are −0.5 C at H-site and +1.5 C at U. The uranium atoms in β-UH3 with the low magnetic moment (0.89 μB), Wyckoff position 2a, have a lower Bader volume than the U atoms in the 6c positions (18.6 compared to 19.3, 19.6, and 23.3 Å3), and also a significantly smaller charge (+1.31 C) than the 6c uranium atoms with the high magnetic moment (+1.72 C) as well as the U atoms in α-UH3 (+1.50 C). These values indicate a significant charge transfer from U to H. The different charge on U atoms yields different orbital moments, while the spin moments are not sensitive. We refer the reader to [63] for more detailed analysis. An important finding is that the 5f occupancy remains in the range n5f = 2.7–2.8 for all the hydrides (and both U sites in β-UH3), so the charge transfer indeed affects only the 6d and 7s states. Numerical experiments with placing Mo atoms at the 2a U position increase the U charge at the 2a position (by 0.2 C), while the 6c positions are much less susceptible. The electron transfer per one U atom therefore increases, which can be tentatively related to the enhancement of TC in alloyed hydrides. Other reasons may include possible effect of small but non-negligible magnetic moments on substituting transition-metal atoms. Ab-initio calculations can give a guidance as moments can be assumed on Zr [60], but their existence should be corroborated by microscopic techniques such as x-ray magnetic circular dichroism (XMCD).
Table 3. Bader volumes and Bader charges Q for the pure UH2, α- and β-UH3, as well as for Mo-alloyed β-UH3 computed with GGA + U method with U = 0.5 eV and J = 0.5 eV.
| Compound | Wyckoff position | Bader volume (106 pm3) | Q(U) (C) | Q(H) (C) |
|---|---|---|---|---|
| UH2 | 4a | 23.3 | +1.34 | −0.67 |
| α-UH3 | 2a | 19.3 | +1.50 | −0.50 |
| β-UH3 | 2a | 18.6 | +1.31 | −0.54 |
| 6c | 19.6 | +1.72 | −0.54 | |
| β-U(Mo)H3 | Mo at 2a | — | +1.50 | −0.50 |
| β-U(Mo)H3 | Mo at 6c | — | +1.70 | −0.50 |
Despite the DFT + U method being certainly successful in describing the electronic structure of uranium hydrides, there are some aspects that are not (and due to the limitations of the method cannot be) modeled accurately. Among these aspects are properties related to the paramagnetic phase or some fine features observed by spectroscopies. The issue with modeling the paramagnet is that the magnetic moments formed in the uranium 5f shells are still there, but they are dynamically fluctuating, which a static method like the DFT + U cannot describe. It can model only ordered magnetic states or an entirely non-magnetic (spin-restricted) state. The non-magnetic state is a very poor approximation for a paramagnet—the energy difference between a ferromagnet and a paramagnet is due to magnetic exchange, which is of the order of kB TC ≈ 15 meV per U atom, whereas it comes out ≈ 0.25 eV per U atom in GGA and ≈ 0.5 eV per U atom in GGA + U [25, 74]. This large energy difference is mainly due to the energy gain associated with the formation of uranium magnetic moments and not with the energy gain due to their ordering. Better approximations of the paramagnetic state available within the DFT framework are methods developed for disordered alloys, namely the disordered local moments (DLM) method based on the coherent potential approximation [89] or a supercell method where the moments are arranged according to a special quasi-random structure (SQS) [90, 91]. Both methods were applied to UH3 with the goal to reproduce the observed spontaneous magnetostriction (expansion of the lattice at the transition to the magnetically ordered state), the DLM state together with some additional simplifications was used in [60], the SQS state was used in [74]. The attempts were quite successful, the DLM model gives, besides the correct order of magnitude of the spontaneous magnetostriction (calculated ωs = 7.5 × 10−3, experiment ωs = 3.2 × 10−3), also a very good estimate of the Curie temperature [21]. An even more accurate model for the paramagnetic phase can be constructed using the dynamical mean-field theory (DMFT), which was recently applied to the paramagnetic states of α- and β-UH3 as reported in [92]. In that study, however, only the paramagnetic states were considered and no geometry optimization was performed, hence the DMFT estimate of effects like magnetostriction remains a task for future work.
7. Electron spectroscopies
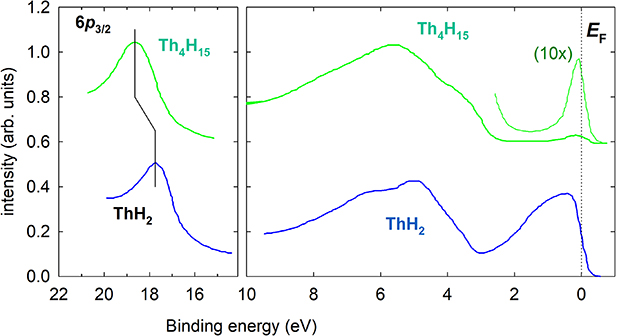
Electronic structure study by photoelectron spectroscopy of both known Th hydrides was performed by Weaver et al [93]. While ThH2 exhibits a Th metal derived band extending 2 eV below EF, Th4H15 has this feature much weaker and also narrower, reduced to a single peak of 0.6 eV FWHM, below which a gap 2 eV wide develops (figure 9). In both cases, an intense emission in the range 3–7 eV binding energy (BE) is attributed to the 6d-1s hybridized states. The work also determined the position of the semi-core Th-6p3/2 states, which are located 0.9 eV deeper below EF than in ThH2, the latter seen at ≈18.0 eV. This was interpreted as a reduction of the work function due to occupation of states located above EF in Th metal. However, the shift of the 6p levels due to H bonding is another (and more likely) reason. While the spectra for Th4H15 in [93] are shifted to lower binding energies assuming that energies of core-level lines should not change between ThH2 and Th4H15, here we present the same data without the energy adjustment. The shift of the 6p3/2 emission can be understood (similar to the 6p3/2 shift between U and UH3 shown below) as an effect induced by the partial transfer of valence Th electrons towards H.
Figure 9. Valence-band photoelectron spectra of ThH2 and Th4H15, obtained using the photon energy hν = 35 eV (right panel). Left panel shows the shift of the 6p3/2 line by 0.9 eV towards higher binding energy [93]. The dotted line denotes the Fermi level.
Download figure:
Standard image High-resolution imageSubstantially more spectroscopic information exists on hydrides of uranium. However, the issue is the high surface reactivity of hydrides, which causes fast oxidation. Therefore, data which do not explicitly state the O concentration have to be taken with caution. For example, the valence-band x-ray photoelectron spectroscopy (XPS) reported on UD3 in [56] exhibits a peak at 2 eV BE, which is, together with the spectral features in the range 5–7 eV BE, characteristic of the 5f2 states in UO2 [94] (see figure 10).
Figure 10. Comparison of XPS spectra of UH3 and U-metal thin films [73] on the background of calculated densities of states using the FPLO fully relativistic method and the LDA functional (dotted lines). While the intensity close below the Fermi level can be attributed mainly to the 5f states, one can notice additional spectral density in the hydride, attributed mainly to hybridized 6d-1s states in the range 4–7 eV below EF. The thin-film data are compared with historical data (cyan line) from [56] and with thin-film data with partial oxidation (black line). For the last spectrum, the O-1s intensity (not shown here) indicates that almost 50% of U is in the UO2 form. The magenta spectrum represents the valence band of UH2 thin film.
Download figure:
Standard image High-resolution imageMore reliable, in terms of lower surface oxygen contamination, are photoemission experiments on in-situ synthesized oxygen-free thin films [95]. The synthesis using reactive sputtering with H2 in sputter gas (Ar) allows to bridge U and UH3 by varying the H2 concentration. Figure 10 reveals that the 5f emission remains actually in the close vicinity of the Fermi level in UH3, while additional feature in the form of a shoulder, formed in the range 4–7 eV, contains, as ab-initio computations show, mostly the hybridized 1s-6d states. One should notice the shift of 6p3/2 line towards higher binding energies in the hydride. This behavior is also in line with theory predictions [73]. Figure 10 also demonstrates that a partial oxidation leads to the development of the emission at 2 eV and to a reduction of intensity close to EF.
It is interesting that energies of deeper core levels do not react to H absorption by such a dramatic shift. However, their shape changes significantly. Figure 11 showing the variations of the U-4f core-level lines demonstrates that the narrow and almost symmetric 4f lines of U metal acquire in the hydrides more asymmetric shape with a lower slope on the high BE side. Moreover, a weak and broad satellite structures, better visible for the 4f5/2 peak, develop upon hydrogenation. Such satellites, related to particular types of screening of the core hole, are a general attribute of core-level spectra when electron–electron correlations are prominent in the valence band [96]. The energy of the maximum of the peaks shifts to higher energies only by 0.2 eV, from 377.4 eV for U to 377.6 eV in both hydrides, which are strikingly similar to each other. The more shallow 5d states react to hydrogenation by a slightly larger shift of 0.5 eV, as shown by the U-5d spectra. The small energy shifts can be qualitatively understood by the fact that the polar bonding does not affect significantly the 5f states, which are more localized in the core than the 6d and 7s states, impacting mainly the more extended 6p states [73].
Figure 11. U-4f core-level spectra of UH2 and UH3 thin films, compared with U metal film at the same experimental conditions (with intensity reduced by 0.5 to fit to the same scale). The small energy shift of the 4f7/2 line is visible in the inset. The UO2 4f7/2 line is added for comparison (upper panel). Comparison of the U-5d spectra for U and UH3 (lower panel) (partly based on data from [73]).
Download figure:
Standard image High-resolution imageThe ultraviolet photoelectron spectroscopy (UPS) of the valence band provides more details (comparing to XPS) especially around the Fermi level. Figure 12 shows that the simple triangular emission increasing up to the Fermi level in U metal is modified in UH3. The maximum is still at or very close to the Fermi level, but a satellite develops at 0.5 eV below EF. The computations reveal that such spectrum is actually reflecting not the ground state density of states (DOS), but the final-state 5f2 multiplets, reached by emitting an electron from the 5f3 ground state. Similarly, NpH3 can be possibly interpreted as 5f3 multiplets, PuH3 as 5f4 multiplets, and Am as 5f5 multiplets, the last two being unresolved [97]. The differences with respect to pure metals are most striking in the case of Pu [97], in which pure metal has most of the emission close to the Fermi level, whereas PuH3 has very little at EF, reflecting the possible loss of metallicity, and the main emission is in a broad maximum at 2.5 eV below EF. One can compare PuH3 with e.g. the HeII spectrum of PuSb [98], which is known for its localized 5f5 configuration, yielding therefore the 5f4 final-state multiplets, but at a lower (by ≈ 0.5 eV) BE. Another difference of PuSb is that the Fermi level is clearly manifested, in agreement with metallic state. For Am with 5f states localized already in pure metal, the main emission is shifted down by ≈1 eV to 3.5 eV below EF, undoubtedly as an effect of polar bonds.
Figure 12. HeII UPS spectra (hν = 40.81 eV) of selected AnH3 compounds, compared with U metal. For this photon energy, the spectra are dominated by the 5f emission. Based on data from [97] and [73].
Download figure:
Standard image High-resolution imageTo justify the interpretation of the spectra in terms of the atomic multiplets, figure 13 shows the results of calculations of α-UH3, which were obtained by our implementation of the DFT + DMFT method described elsewhere [99, 100]. Generally, the DFT + DMFT method requires larger values of the 5f–5f Coulomb interaction parameters than the DFT + U method to yield comparable results [99, 101]. Here we adopted Coulomb U = 1.0 eV and Hund J = 0.6 eV to be in line with the DFT + U results reported in the previous section and using U = 0.5 eV and J = 0.5 eV. The comparison to the experimental XPS and BIS [73] in figure 12 indicates that this setting places the uranium 5f states at the correct energies. Moreover, the theory reproduces the shoulder at 0.5 eV BE resolved in UPS [73, 95, 97], which is the expected 5f3 → 5f2 multiplet transition. We were able to prove this assignment by performing a series of calculations with the hybridization between the 5f states and the other electronic states varied from zero (the atomic limit where the multiplet transitions are exact) to the realistic UH3 strength. We did indeed see that one of the multiplet transitions continuously evolves from the atomic limit to the feature seen in figures 12 and 13. We note that in the DFT + DMFT spectra reported in [92], the 0.5 eV feature has a much weaker intensity than in our calculations presented here. It may possibly be due to a much larger Coulomb U = 5.3 eV employed in [92]—we verified that the intensity of this feature is reduced with increasing U, but we did not go as far as U = 5.3 eV in our investigation, since we consider this value unrealistically large for UH3.
Figure 13. Valence-band spectra for the paramagnetic phase of α-UH3 computed with LDA + DMFT are compared with experimental spectra: UPS (photon energy 40.8 eV), XPS (photon energy 1486.6 eV), and BIS [73]. The experimental spectra are shifted along the vertical axis for clarity. The theoretical spectra are constructed as linear combinations of the orbital-resolved densities of states weighted with appropriate photoionization cross sections [102]. Gaussian broadening with FWHM 0.27 eV (UPS) and 1.3 eV (XPS and BIS) is applied to the theoretical spectra to model the instrument resolution.
Download figure:
Standard image High-resolution imageWe performed analogous DFT + DMFT calculations also for the hexagonal (P63/mmc) PuH3 at the experimental structural parameters [103–105] and with Coulomb parameters U = 4.0 eV and J = 0.6 eV. The shape of the computed valence-band spectra (figure 14) reproduces the shape of the experimental UPS [97] quite well, only the spectrum as a whole appears to be shifted by about 1 eV to lower binding energies. This shift is likely a combination of two effects: (i) the underestimated BE of the H-1s bands (hybridized with the U-6d states), which is inherent to the LDA functional, on top of which the DFT + DMFT is built (and which is visible also for UH3 in figure 13), and (ii) somewhat underestimated Coulomb U. The 5f component of the computed spectrum does not resemble the atomic multiplet transitions as closely as in UH3 due to a larger mixing of the U-5f states with the H-1s states as their binding energies overlap, which is a situation similar to oxides [99]. Another DFT + DMFT study of PuH3 was reported in [106] where the calculated valence-band spectra of a cubic PuH3 and PuH2 were compared.
Figure 14. Valence-band spectra for the paramagnetic phase of hexagonal PuH3 computed with LDA + DMFT are compared with experimental UPS (photon energy 40.8 eV) [97]. The experimental spectra are shifted along the vertical axis for clarity. The theoretical spectra are constructed as linear combinations of orbital-resolved densities of states weighted with appropriate photoionization cross sections [102]. Gaussian broadening with FWHM 0.4 eV is applied to the theoretical spectra to model the instrument resolution.
Download figure:
Standard image High-resolution imageIn the computed spectra of the paramagnetic phase of PuH3 (figure 14), there is very little spectral weight appearing in the vicinity of the Fermi level, nevertheless, the electronic structure is metallic since one band of the Pu-6d character crosses the Fermi level near the K point, forming an electron pocket. In the same time, several DFT + U studies indicated a gapped electronic structure for magnetically ordered phases of the hexagonal PuH3 [107, 108]. Note that in [108], the P63/mmc structure was found dynamically unstable and an alternative hexagonal structure (P63 cm) was suggested instead. In the case of a hypothetical cubic PuH3, the computational results are inconclusive since insulating [109] as well as metallic [36] band structures were reported, although essentially the same DFT + U approximations were employed.
8. Hydrides of actinide compounds
Besides pure actinide metals, hydrides can be prepared from many binary or ternary intermetallic compounds. Interest in such systems is related to exploring possibilities of hydrogen storage (without limitations of e.g. high surface reactivity of UH3). Fundamental motivations dwell in possibilities of fine tuning of electronic properties of compounds, which typically do not exhibit such pronounced volume expansion as hydrides of pure actinide elements. Particularly interesting is to add the H absorption and concomitant volume expansion as tuning parameters in large systems of ternary compounds (known mainly for uranium), where the electronic structure can be modified by varying ligand atoms in the same crystal structure type. In such systems, several possible scenarios of e.g. onset of magnetic ordering can be investigated, extracting general features. Interesting opportunities are provided in situations, in which the H absorption gives an anisotropic lattice response. An expansion in one direction can be partly compensated by a lattice contraction in special cases. Although the H absorption is not easily achievable in all interesting cases, it is still quite common (depending on non-f components) to allow systematic studies. Synthesis by direct exposure to H2 gas using pressures of 10 MPa has been successful in numerous cases. We can expect that the polar bonding can play a supportive role for magnetism as in binary hydrides, although presence of other constituent metals can blur the picture to some extent and this aspect of hydrides of intermetallic compounds has not been so far tackled by computations in a systematic way.
8.1. Hydrides of ternary compounds
Quite systematic work has been performed on families of compounds generally denoted as UTX and U2T2X, where T stands for a transition metal and X for a p-metal. Among the UTX compounds, the most abundant is the ZrNiAl structure type, for which the H absorption is restricted to smaller sub-groups, one of them including UNiAl, UNiGa, and UNiZn. UNiAl has an antiferromagnetic ground state (TN = 19 K) [110]. Its hydride remains antiferromagnetic, TN increases up to ≈100 K for ≈2 H/f.u. [111]. The maximum H concentration of ≈2.3 H/f.u. exceeds that of isostructural rare earth compounds, in which 1.4 H/f.u. is apparently the upper limit [112]. This is enabled by a more extended structure modification with three (or more) different H positions, identified by neutron diffraction on the deuteride [113]. (Somewhat different structures were suggested in [114, 115]. The last analyses indicate that the structure of the full UNiAl hydride has actually a higher symmetry and corresponds thus to the LiBaSi structure type, which is an ordered variant of the AlB2 type [116].) The small compression in c and large expansion in a gives a volume expansion of 12.9%. An interesting fact that it changes the basic U–U coordination (nearest U–U links in the basal plane in UNiAl are switched to the c-axis in the hydride) was used to disclose the impact of the f–f bonding directionality on anisotropy of elastic properties. Indeed, linear compressibility in the hydride is higher along c, while the a-direction was much softer in all UTX non-hydrogenated compounds with the ZrNiAl structure type. Similar cross-over happens also for the linear thermal expansion coefficients [117]. Interesting finding is that the high Sommerfeld coefficient γ = 164 mJ mol−1 K−2 of UNiAl is reduced to 74 mJ mol−1 K−2, clearly due to stabilization of sizeable U moments in the hydride, shifting the material from the proximity of the verge of magnetic order [118]. Such values can be compared with γ = 7 mJ mol−1 K−2 in LuNiAl without f-electrons and mere 2 mJ mol−1 K−2 in its hydride [119]. The H absorption decreases when Ni is substituted by other transition metals, but the impact of H on magnetic properties can still be significant. In the pseudo-ternary systems UNiAl-UFeAl without hydrogen, the antiferromagnetism of UNiAl is rapidly suppressed. After a concentration gap 10%–20% Fe a ferromagnetic range appears, possibly due to the 3d moments involvement, which extends to 70% Fe. Although the capability to absorb H decreases with the Fe substituted by Ni (registered only up to 30% Fe), it is evidently not much reducing the volume expansion, and the impact on magnetism remains dramatic. Hence it still gives TC = 90 K for UNi0.7Fe0.3AlH0.8, with volume expansion 7.3%. (Pure UNi0.7Fe0.3Al has TC = 15 K). UNi0.8Fe0.2Al is non-magnetic, UNi0.8Fe0.2AlH2.0 ferromagnetic with TC = 98 K [120, 121]. On the basis of analysis of 57Fe Mössbauer spectroscopy, in particular of the isomer shift being close the α-Fe in the hydrides, it was suggested [121] that the 5f-3d hybridization is reduced upon hydrogenation. Analogous development was observed also for the Co substitutions [122].
All details of crystal structure of UNiGa are very similar to UNiAl, but the U magnetic moments are large and stable (1.4 μB [123] compared to a long wavelength modulated spin density wave in UNiAl, which reaches 1.25 μB at its maximum [124]). UNiGa orders antiferromagnetically below 39.5 K. In its hydride UNiGaH1.5 the ordering temperature increases only to about 50 K. Crystal structure analysis reveals that the structure modification differs from the UNiAl hydride case. It undergoes an orthorhombic distortion, which actually reduces, despite the volume expansion of 8.6%, the U–U distances from 348 pm in UNiGa to 337 pm in UNiGaH1.5. The Sommerfeld coefficient actually increases from γ = 59 mJ mol−1 K−2 in UNiGa to 76 mJ mol−1 K−2 in its hydride, so we can conclude that stable U moments formed already in the precursor intermetallic are affected much less than if the precursor is non- or weakly-magnetic [116]. The non-magnetic precursor is e.g. UNiZn with paramagnetic ground state. The smaller atomic radius of Zn compared to Ga or Al brings a stronger 5f-p hybridization. As a hydride with the stoichiometry UNiZnH2.3, i.e. analogous to UNiAlH2.3, it becomes antiferromagnetic (TN = 55 K) [125]. The structure corresponds to the AlB2 type with the random Ni/Zn occupation of the B sites. The γ-value is similar in both systems, 94 mJ mol−1 K−2 in UNiZn and 100 mJ mol−1 K−2 in the hydride, but it is likely that those values are located on opposite side of a maximum of γ, located at the verge of magnetism, where the electron system is represented by a system of quasiparticles with high effective mass (see figure 15).
Figure 15. Schematic representation of localization variations affecting the Sommerfeld coefficient γ, which is dramatically enhanced around the onset of magnetic order in actinide and anomalous lanthanide systems. Individual compounds are placed rather arbitrarily on the Localization axis, reflecting presence and stability of U magnetic moments. Based on data from [116] and [125]. Reprinted from [27], Copyright (2022), with permission from Elsevier.
Download figure:
Standard image High-resolution imageBesides the compounds with T = Ni, H absorption was detected for UPdIn, which is a heavy fermion antiferromagnet (TN = 21 K) with γ = 280 mJ mol−1 K−2 [126], i.e. even higher than in UNiAl. TN of UPdInH0.7 dramatically increases to 80 K, while γ drops to 30 mJ mol−1 K−2. The size of the moments increases from 1.5 to 2.5 μB per U atom. It is interesting that the lattice expansion along the a-axis (Δa/a = −0.2%) and along the c-axis (Δc/c = +3.2%) is opposite to UNiAl [127].
The highest ordering temperatures within the group of UTX compounds with ZrNiAl structure type were found in ferromagnets from the system UCoSn-UFeSn. The increments due to hydrogenation are, however, relatively small. UCoSn has TC = 83 K, UCoSnH1.4 with volume expansion 3.24% (concentrated mostly in a) has TC = 102 K [128]. The TC values increase with Fe substitutions for Co, with the structure stability limited to 20% Fe. The TC increment due to hydrogenation decreases as a function of Fe concentration. This happens despite invariable volume expansion, which suggests that the expansion is not the primary driving mechanism and the actual H concentration may be more important. The highest TC = 108 K was found in the hydride of UCo0.85Fe0.15Sn. The TC increment is ΔTC = 10 K in this case [128]. The dilution of U sublattice in UCoSn by Th leads naturally to decrease of TC and the long-range order disappears at ≈60% Th. The respective hydrides follow the same tendency with gradually reduced ΔTC, hence the verge of magnetic order remains around 60% Th, as well [128].
Other group of UTX compounds studied systematically with respect to the impact of hydrogen is the UT(Si,Ge) family with the orthorhombic TiNiSi structure type. Full H content giving the stoichiometry UTXHx with x approaching two leads to the hexagonal structure of the ZrBeSi type, one of the ternary variants of the AlB2 type [129]. It is hence another example, besides e.g. UNiAl, of enhancement of symmetry to the AlB2 type of structure. As in other cases of U materials close to the verge of magnetism, where emergent phenomena around the quantum critical point are observable, the effect of H can bring very original information. Here a standard tuning tool in the field of quantum criticality is hydrostatic pressure, compressing the volume. Although the expansion in hydrides could be naively expected as corresponding to a negative pressure, it is not always the case.
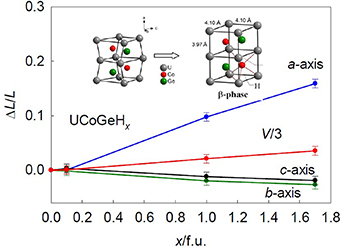
In the case of UCoGe, the weak itinerant ferromagnetism (TC ≈ 3 K) coexists with unconventional superconductivity (Tc ≈ 0.6 K) mediated by spin fluctuations [130]. As the ferromagnetism disappears under hydrostatic pressure, one would expect higher moments and ordering temperatures upon hydrogenation. But experiment showed just the opposite tendency and its reason was disclosed by the high-pressure structure study, indicating that the directionality of U–U bonding makes the compression strongly anisotropic [131]. However, the anisotropic reaction following small H absorptions is of different type, and both H absorption and pressure lead to shrinking of the U–U links important for magnetism. This study is using a small tuning within the range, where a limited amount of H is dissolved in the matrix of the parent. This so-called α-hydride range exists up to the concentration UCoGeH0.1. The orthorhombic TiNiSi structure is preserved, which allows a direct comparison with pure UCoGe.
The hexagonal β-hydride, synthesized at higher H2 pressures, has the estimated stoichiometry UCoGeH1.7. It becomes ferromagnetic with TC = 50 K, but the magnetization remains small, corresponding to 0.05 μB per U atom [132]. The γ-value is approximately doubled in the hydride (≈100 mJ mol−1 K−2) compared to the pure UCoGe with 65 mJ mol−1 K−2 [133]. From the non-magnetic side of the UTGe compounds, the hydrogenation study has been performed for UFeGe, a weak paramagnet with γ= 12 mJ mol−1 K−2 [134]. The hydride UTGeH1.7 has γ enhanced to 36 mJ mol−1 K−2. Despite the volume expansion of 6%, no magnetic ordering could be detected, but magnetic susceptibility becomes higher and more T-dependent. The variations of magnetism within the UTGe (and UTGeHx ) series reflect the underlying mechanisms responsible for modifications of the electronic structure. The mutual hybridization of the Fe-3d and U-5f states is able to suppress both the 5f and 3d magnetism, as the 3d and 5f states overlap around EF. This is a dramatically different situation compared to the rare earths with localized 4f states, which do not contribute to the 3d band broadening. Here the 3d magnetism provides high ordering temperature and the 4f-3d exchange (via the 5d states) gives a robust interaction between the sublattices and large magnetizations. For uranium in a contact with Fe, typically neither the volume expansion usual in hydrides and the related higher U–U spacings (from 345 pm in UFeGe to 367 pm in UFeGeH1.7) nor the polar bonding provides a route to magnetism. The only opportunity is to reduce the 5f-3d hybridization by going from Fe to Co and Ni, but then also the 3d contribution to magnetism is diminished and critical temperatures cannot be very high. As demonstrated also in U(Co,Fe)SnHx described above, the effect of hydrogen can be high in an intermediate stage. Besides UCoGe, an interesting case is URhGe, a weak ferromagnet (TC = 9.5 K [133]), which coexists with unconventional superconductivity appearing in the millikelvin range [135]. The high H2 pressures of 150 bar yielded only limited H concentrations of URhGeH0.3, not sufficient to convert the TiNiSi structure type into the ZrBeSi type. The small volume expansion of 1.3% leads to an increase of TC to ≈17 K, while spontaneous magnetization increases from 0.2 μB/f.u. to 0.38 μB/f.u. UNiGe representing a more local-moment system is antiferromagnetic below TN = 50 K and has a rather low γ = 27 mJ mol−1 K−2 [133]. The parallel alignment of moments reached in high magnetic field above 40 T indicates magnetization approaching 1.5 μB per U atom [136]. The full hydride UNiGeH1.2 exhibits a ferromagnetic order below ≈100 K. The size of moments is difficult to estimate, as there is only a slow tendency to magnetization saturation in fields exceeding 50 T. As in many other cases, one has to assume a statistical occupancy of H sites inside the U3Ni tetrahedra, the full occupancy of which would yield UNiGeH2. The randomness leads to local variations of magnetic exchange as well as of easy magnetization direction, as studied computationally for U2Ni2Sn (see below). The inhomogeneities on atomic scale thus lead to an effective non-collinear ferromagnetism or similar defected antiferromagnetism without complete cancellation of individual sublattices. This fact is likely to be more pronounced in local moment situation than in broad band magnetics. The γ-value increases to 70 mJ mol−1 K−2 [137].
The analogous silicides UTSi are less amenable to hydrogen absorption, likely due to their smaller unit cell volumes. The types of structure development is the same as for the germanides, but the number of known hydrides is smaller. UNiSi is analogous to UNiGe, it orders antiferromagnetically below TN = 85 K [138]. Its hydride UNiSiH1.0 becomes a ferromagnet (or rather uncompensated antiferromagnet) with TC = 98 K. If the hydride is exposed to a hydrostatic pressure, the hexagonal ZrBeSi structure remains stable (at least to p = 38 GPa), while TC has a decreasing tendency with increasing p up to 1.2 GPa [139]. Similarly, the TN value increases from 31 K in UPdSi to 46 K in UPdSiH1.0 [138]. In this case the TN value increases up to 52 K under 1.2 GPa of hydrostatic pressure [139]. The fact that one encounters such diverse reaction of the two hydrides to pressure, while the volume expansion due to hydrogenation, ΔV/V ≈ 7–8%, is quite similar, suggests that the changes of the magnetic ordering temperatures due to hydrogenation are not directly coupled to the volume expansion. However, as observed in the case of UCoGeHx , the anisotropy of compressibility, not reflecting the anisotropic expansion due to H absorption (figure 16), brings additional degrees of freedom, which make any analysis in terms of atomic volume oversimplified.
Figure 16. Reaction of crystal lattice of UCoGe to the H absorption (given by H concentration x per formula unit) is highly anisotropic. While the volume expands, the lattice actually expands only in the a-direction and shrinks in b and c, which reduces the shortest U–U distances. Interestingly, the application of hydrostatic pressure gives indeed a dominant compression in a, but b and c are somewhat reduced as well. Hence the concept of hydrogenation as a negative pressure has to be taken with caution. For details see [131, 132].
Download figure:
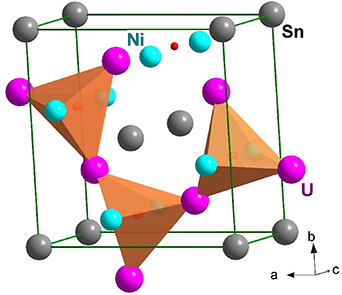
Standard image High-resolution imageA systematic investigation has been performed over the system of actinide compounds denoted as An2T2X. Besides An = U [140, 141] they are known also for Np [140], as well as Pu and Am [142], but the H absorption has been explored only for the U-based species. Similar to other U compounds, the hybridization with the transition-metal d-states contributes to 5f delocalization and moments destabilization when proceeding to the left from the end of 3, 4, 5d series, while non-transition elements X contribute by the 5f-p hybridization. The last effect is stronger for small (light) X elements, while the heavy and larger X atoms may work opposite, inflating the structure and enhancing all inter-atomic distances. This development can be further supported by the H-driven expansion in hydrides, and we can expect to some degree also the positive effect of release of the 5f states from the 5f-6d hybridization in analogy with U binary hydrides, where the 6d-1s hybridization and polar bonds represent an important ingredient. As a result, the hydrides shift the borderline between paramagnetic and ordered systems. The H absorption was recorded in an extended set of compounds, which allows us to deduce general tendencies of its impact on electronic properties. An advantage is that apparently mostly a single H site is occupied, reaching the theoretical limit of two H atoms/f.u., and the lattice symmetry of the metal sublattice remains unchanged. The compounds are tetragonal, crystallizing in the Mo2FeB2 structure type (ordered derivative of the U3Si2 type), with H atoms occupying mostly (or exclusively) the U3-T tetrahedra, as shown for the case of U2Ni2Sn, where the D positions were identified by neutron diffraction on deuteride [143] (see figure 17). The D positions in the actual sample U2Ni2SnD1.8 were determined as close to the basal plane of U atoms (the offset along the c-axis is only 0.0339c), which prevents simultaneous occupation of two adjacent tetrahedra sharing one of the faces. The U–D distances of 218 pm are in this case somewhat smaller than 232 pm in UH3, which may be interpreted as smaller charge transfer to D, related to the presence of Ni and Sn.
Figure 17. Perspective view of the tetragonal crystal structure of U2Ni2Sn hydride along a direction close to [001]. H atoms shown as a small red dot are located inside the marked U3-Ni tetrahedra.
Download figure:
Standard image High-resolution imageThe influence of the 5f-d hybridization can be illustrated on the case of the U2(Ni1-x Fex )2Sn pseudo-ternary system. The antiferromagnetism found in U2Ni2Sn (TN = 25.5 K) [144] is lost around 20% Fe and U2Fe2Sn is a weak Pauli paramagnet [145]. The hydride U2Ni2SnH1.8 has TN shifted up to 87 K [146]. The Fe substitution gives enhanced volume of the respective hydrides, and it is probably this aspect which again yields, in a broad concentration range, a magnetic order, ferromagnetic in this case, with TC values reaching 38 K in maximum around 60% Fe [145]. Ab initio calculations suggest that the ferromagnetic order may be promoted by the ferromagnetic coupling between Fe moments [147]. This may reflect a more general situation, in which U magnetism setting in at a sufficiently high volume can exhibit a supporting interplay with the Fe moments. This would be in a clear contrast to a low volume situation, in which the 5f and 3d hybridization leads to a destruction of both types of magnetism.
The γ-coefficient in the precursors steeply increases with increasing Fe concentration from 172 mJ mol−1 K−2 in U2Ni2Sn (187 mJ mol−1 K−2 determined from later single crystal data [144]) to 430 mJ mol−1 K−2 for 20% Fe, where a non-Fermi liquid behavior with an upturn in C(T)/T indicates proximity to the quantum critical point. On a fine concentration mesh, the upturn rises only in about 2 at.% wide range of Fe concentration below 20% Fe. A decrease is seen also on the non-magnetic side [145]. For the hydrides, the γ-values are systematically somewhat smaller, still about γ = 280 mJ mol−1 K−2 is reached in U2(Ni0.8Fe0.2)2SnH1.8, while γ = 105 mJ mol−1 K−2 in U2Ni2SnH1.8.
The anisotropic H-driven expansion (predominant in the basal plane in U2Ni2Sn; Δa/a = 2.4%, Δc/c = 1.8%, ΔV/V = 6.6%) can impact the local coordination of U atoms responsible for the magnetic anisotropy. Namely, the easy magnetization direction tends in U intermetallics to be perpendicular to the nearest U–U links, concentrating the 5f bonding contribution in f-band systems [136]. This two-ion bonding anisotropy forces the U moments in U2Ni2Sn to align along the c-axis, as the nearest U neighbors are located in the basal plane (at 355 pm), but larger expansion of the basal plane of the hydride makes the distance along c practically equal (≈ 375 pm). This may switch the easy magnetization direction from the c-axis to the basal plane, as suggested by neutron diffraction [143]. Calculations [148] indicate that the reality may be more complicated, as the U moments cant out of the c-axis, following the reduction of local symmetry, when the H position inside the U3Ni tetrahedra is occupied. As only 50% of equivalent positions is occupied (probably randomly) in U2Ni2Sn, this leads to randomization of the direction of U moments.
A complete cross-over of U–U spacings due to hydrogenation was detected at UNiAl mentioned above. The expansion in a and contraction in c gives the shortest U–U spacing of UNiAlD2.1 along c, while it was within the hexagonal basal plane in pure UNiAl. As the U–U directions of U–U bonds play a decisive role not only in direction of magnetic moments but also in anisotropy of elastic moduli and thermal expansion, it is no surprise that the c-direction becomes the softer one [117] in the hydride while all investigated known UTX compounds with the ZrNiAl structure have the compression under hydrostatic pressure strongly concentrated in the a-direction [149].
Similar to U2Ni2Sn, an enhancement of TN from 19 to 60 K was found also in U2Ni2InH1.9 [146]. U2Co2Sn, which is (without hydrogen) at the verge of magnetic order with γ = 350 mJ mol−1 K−2 in the heavy fermion range [150], can give a weak ferromagnetic order at TC = 33.5 K in the α-hydride range with ΔV/V = 1.4%. The β-hydride with ΔV/V = 8.1% and approximate composition U2Co2SnH1.4 is then antiferromagnetic below 27 K [151]. Its counterpart, U2Co2In, is a weak Pauli paramagnet, while the hydride U2Co2InH1.9 is reminiscent of U2Co2Sn without hydrogen, with an upturn in C(T)/T with high γ = 244 mJ mol−1 K−2 and a large increase of magnetic susceptibility at low temperatures indicating proximity to magnetic ordering. Indeed, U2Co2Sn and U2Ni2InH1.9 have very similar dU–U values of 350.5 pm and 350.7 pm, respectively. This is much higher distance than in U2Ni2In (343.4 pm) and much lower than in magnetic U2Co2SnH1.4 (358.1 pm) [152]. The possibility to fine tune electronic structure by relatively small (comparing e.g. to U trihydrides) concentrations of hydrogen hence indicates that the volume changes are the primary mechanism affecting the U-5f magnetism around the quantum critical point.
Experiments with H as a probe into unconventional superconductor UPd2Al3 (Tc = 2 K), which in addition orders antiferromagnetically at TN = 14.5 K, were reported in [153]. Increasing the H concentration (up to UPd2Al3H1.3) shifts the Néel temperature down and magnetic entropy eventually forms a pronounced upturn below 10 K, yielding γ = 650 mJ mol−1 K−2. This value is only slowly reduced by magnetic fields, but it remains an open question whether such high value indeed reflects high effective masses of interacting electrons or if some kind of short-range order remains. A similar suppression of critical temperatures was found for superconductivity, but its traces could be found up to x = 0.5 H/f.u. Unfortunately, no attempt to determine the H positions or to define homogeneity was mentioned. The structure information is limited to the unit cell expansion by 0.75% (Δa/a = 0.0052, Δc/c = −0.0031).
8.2. Binary actinide intermetallics
Besides the large groups of ternary compounds, there are interesting results obtained at individual ad hoc hydrogenation cases of binary intermetallics. One of them is U3Si2, with tetragonal structure closely related to the '221' compounds mentioned above. This material has been used as a nuclear fuel and its easy hydrogenation brought concerns about its 'accident tolerant' character [154, 155]. Pure U3Si2 is a weak Pauli paramagnet, its hydride U3Si2H1.8 is a spin fluctuator. Its location at the onset of magnetism is evidenced by the very high Sommerfeld coefficient of 500 mJ mol−1 K−2 [156].
Although Laves phases of U were found to be inert with respect to H2 in pressures of ≈10 MPa (being very different from the rare-earth counterparts), it was shown [157] that the hydrogenated cubic Laves phase UTi2Hx can be synthesized via a high-temperature route. The remarkable fact is that the compound UTi2 does not exist without hydrogen, with Ti being a too large atom, coming out of the possible range around the ideal ratio of atomic radii for AB2, namely rA/rB = 1.225. The existence of the UTi2Hx hydride can be rationalized as reflecting the ratio of (U + H) on one side and Ti on the other. The strong bonding of U and H thus effectively increases the atomic radius of the A atom. Unlike UH3 alloyed with Ti, where H positions in U3Ti tetrahedra can be assumed, the particular Laves phase exhibits a partial occupation of U2Ti2 and UTi3 tetrahedra, reflecting the affinity of Ti to H.
Interesting variations of magnetic properties can be obtained when changing the H concentration, possible between UTi2H5 and UTi2H6, giving the respective lattice parameter a = 884.8 pm and 885.8 pm. While UTi2H6 is a ferromagnet with TC = 54 K [158], UTi2H5 is a spin fluctuator close to the verge of magnetic ordering, indicated by the lack of magnetic order and very high γ = 256 mJ mol−1 K−2, which classifies the hydride as a mid-weight heavy fermion [159]. Although the U–U spacing of 367.5 pm, exceeding the Hill limit 340–360 pm [1], can be sufficient for stabilization of U magnetic moments and their ordering, the Ti 3d states located roughly at the same energy as the 5f states tend to destabilize them by the 5f-3d hybridization. This hydride could be prepared as a monolithic polycrystal, which enabled to deploy a whole suite of transport techniques, proving the spin fluctuation phenomena. There is also an effect of stochastic occupation of H sites, giving certain atomic disorder. This was used to demonstrate how such atomic disorder can indeed yield a linear dependence of the electrical resistivity at low temperatures. Such deviation from the conventional Fermi liquid aT2 behavior was in the past often interpreted as due to low dimensionality of magnetic interactions in situation close to the quantum critical point. The present data reveal that predictions about the effect of disorder in the 3D case are correct [160].
The monolithic form of UTi2H5 allowed a study of a whole suite of transport properties (thermal conduction, Seebeck coefficient), which exhibit a broad anomaly in the range 220–260 K. It has also a fingerprint in the heat capacity and thermal expansion, which suggests that H lattice melting phenomenon takes place in this temperature range, being analogous to e.g. other Laves phase hydrides, such as TbMn2H2 [161].
Actinide compounds with the 5f states involved in metallic bonds with other elements may tend to increase the elastic energy needed for the volume expansion, which makes the hydrogenation more difficult. This can explain why no uranium Laves-phase hydrides with Fe, Co, or Ni have been reported, in contrast to rare-earth based isotypes.
Hydrides of Th compounds with little or no 5f occupancy should be therefore easier to form. There is an interesting information on Th systems with transition metals. As Th has no magnetic moments, the properties are then dependent on the transition metal component T, which has likely the respective d-states hybridized with the 6d states of Th. The reaction to H absorption is then similar to transition-metal systems, which are sensitive to volume expansion similar to the 5f systems (the d-states are band-like), but in this case the support of magnetism is limited by the loss of metallicity for higher H concentrations [27]. The presence of Th may possibly postpone the onset of insulating state, as the Th bonding to H can leave the T sublattice partly intact. In addition, the 6d-1s hybridization in the hydrides can help to release the 6d hybridization with the transition metal d-states. Hence a typical situation is that a Th-T compound is non-magnetic despite high amount of T elements, and hydrogenation is enforcing a magnetic ground state. This happens e.g. in Th2Co7, which could be studied in a single crystal form. It is a paramagnet, while Th2Co7H5 with ΔV/V = 17.7% is antiferromagnet with TN = 90 K. An interesting feature is the negative spontaneous magnetostriction, with both a and c of the hexagonal structure reduced below TN [162].
A large amount of H can be absorbed by Pauli paramagnet Th7Fe3, which has, similar to Th7Co3 and Th7Ni3, a superconducting ground state. The hydride Th7Fe3H30 with undefined crystal structure was reported to be ferromagnetic at TC = 325 K, the spontaneous magnetization corresponds to 1.4 μB per Fe atom. The Co and Ni compounds with lower H concentrations (21 and 24 H atoms/f.u., respectively) remain paramagnetic [163]. However, later on it was found that the hydride of Th7Fe3 disproportionates into Th4H15 and an Fe-rich Th-Fe compound, which is likely responsible for the ferromagnetism [164].
Analogously, the Pauli paramagnetic state of Th6Mn23Dx turns into a ferromagnet with TC = 329 K for x = 30. As Y6Mn23 is ferrimagnetic, one can suppose that the non-magnetic state in the Th counterpart is related to the tetravalent state of Th, namely to the 6d states bonding with the 3d states of Mn. Removing this particular bonding ingredient in the hydride is then the detail responsible for its strong magnetism [165].
Th2Fe17, which is naturally ferromagnetic due to the very high Fe content (TC = 327 K) has TC enhanced to 471 K in Th2Fe17H5 [166]. Further examples of Th-based hydrides can be found in [167].
9. Polyhydrides and superconductivity under pressure
The observation of conventional (phonon-mediated) high-temperature superconductivity in H3S [168] spurred computational investigations of new phases of other hydride systems at high pressures, including hydrides of actinium [169], thorium [170], uranium [68, 69, 170, 171], and plutonium [172]. These investigations combine crystal-structure searching methods with structural relaxations and electronic structure calculations within DFT. Most of the listed studies employ evolutionary structure searches using the universal structure predictor: evolutionary xtallography (USPEX) algorithm, the remaining two [171, 172] predict the crystal structures using the particle swarm optimization algorithm. To verify the dynamical and mechanical stability of the predicted phases, their phonon spectra and/or elastic constants are computed as well.
A very rich composition-pressure phase diagram was predicted for each of the Ac–H, Th–H, U–H and Pu–H binary systems, the U–H case is sketched in figure 18 for illustration. Among Ac–H and Th–H, several phases with very high superconducting transition temperatures Tc were identified, with the highest Tc being found for AcH10 and ThH10 (see table 4 for details). These hydrides appear to be cousins to LaH10, which was recently experimentally demonstrated to be superconducting up to 260 K at pressures around 180 GPa [173, 174]. The highest Tc among uranium hydrides was estimated for UH7 [68] (table 4), whereas all identified plutonium hydrides were found magnetic, including Fm
 m-PuH10 expected to be stable around 200 GPa, and therefore not superconducting [172].
m-PuH10 expected to be stable around 200 GPa, and therefore not superconducting [172].
Figure 18. Computationally determined composition-pressure phase diagram of the U–H binary system adopted from [68]. The most hydrogen-rich phases (U2H17 and UH9), as well as UH17 identified in [171], are stable only at considerably larger pressures and thus not shown in the figure. The Cmcm-UH3 phase reported in [69] was added in a different color (green).
Download figure:
Standard image High-resolution imageTable 4. Theoretically predicted hydrides of actinium, thorium, and uranium with high superconducting transition temperature Tc. The hydride with the highest Tc as estimated by the Eliashberg theory is shown for each of the AcHx , ThHx , and UHx families.
| Hydride | P (GPa) | Tc (K) | Source |
|---|---|---|---|
R
 m-AcH10
m-AcH10
| 200 | 226–251 | [169] |
Fm
 m-ThH10
m-ThH10
| 100 | 220–241 | [170] |
| P63/mmc-UH7 | 20 | 44–54 | [68] |
The study of uranium hydrides [68] was complemented with high-pressure experiments (up to 103 GPa) using laser-heated diamond anvil cells. A number of distinct phases were observed but their unequivocal identification was difficult due to a very limited control over the composition—the hydrogen content could be only estimated by comparison of measured and calculated unit cell volume at a given pressure. Of the new phases, the identification of the P63/mmc-UH7 was the most convincing.
10. Summary and perspectives
Our review, by far not complete and reflecting personal bias of the authors, has been conceived to summarize recent progress in the field of actinide hydrides. The sheer volume of the findings summarized here may suggest that many decades since the discovery of UH3 and other actinide hydrides, a thorough understanding has been achieved. In reality, it is not the case and a unifying picture started to emerge only recently, stimulated by achievements in synthesis (alloyed hydrides), experiments (high pressures, advanced electron spectroscopies on thin films), and new powerful computation methods (DFT + U, DFT + DMFT techniques). Such new tools help to specify (or bracket) the behavior of the 5f states in U-hydrides, which is not entirely band-like but the localization is not achieved either. Their proper description has to involve magnetism and orbital moments in particular. The finding that a polar bonding in metallic state can yield pronounced magnetic properties can be instrumental in exploring U-based magnetics with high ordering temperatures.
Advanced calculations have provided predictions of various characteristics, such as detailed values of charge transfer, spin and orbital moments, their non-collinearity in β-UH3, or phonon dispersion relations. They still remain to be confirmed, which is not trivial with materials, which will be probably never prepared as excellent single crystals and which are strongly reactive in air. The development of thin-film technologies (reactive sputter deposition) can provide suitable samples for techniques as x-ray absorption and emission spectroscopies or XMCD. Such thin-film techniques may also provide possible functional elements, like a sandwich of ferromagnetic UH3 and a paramagnet with a strong spin–orbit coupling. However, the mobility of H may be an issue if a sharp interface is required.
The potential of U metal as a hydrogen storage medium, used so far for storage of tritium, can be certainly utilized also for storing H in stationary applications as an economy option considering the current surplus of depleted uranium. The temperature of full desorption, 727 K (450 °C), which is somewhat higher compared to conventional media, such as LaNi5, could be possibly reduced by alloying or using some of U-rich compounds. On the other hand, the high desorption temperature gives also the capability to absorb H directly reacting with H2 even at elevated temperatures [175].
Besides storage of H and its isotopes, hydrogen purification or even nuclear fuel applications, one can see a potential in high (room) temperature superconductivity. Although extreme pressures needed for synthesis are prohibiting for any practical use of polyhydrides known so far, one has to realize that the focus has been on hydrides of pure elements until now, and the realm of hydrides of compounds has not been explored at very high pressures at all.
Acknowledgments
This paper could not be written without help and input of many colleagues and students. In particular, discussions and help of Leonid Sandratskii, Thomas Gouder, Martin Diviš, Ilja Turek, Alex Kolomiets, Khrystyna Miliyanchuk, Silva Černá-Mašková, Vova Buturlim, Alexandra Koloskova, Zhenia Tereshina-Chitrova are acknowledged. The work has been supported by the Czech Science Foundation under the Grant No. 21-09766S. DL acknowledges support by the project e-INFRA CZ (ID:90140) by the Ministry of Education, Youth and Sports of the Czech Republic.
Data availability statement
The data cannot be made publicly available upon publication because they are not available in a format that is sufficiently accessible or reusable by other researchers. The data that support the findings of this study are available upon reasonable request from the authors.