Analytical Solutions for Gravitational Potential up to Its Third-order Derivatives of a Tesseroid, Spherical Zonal Band, and Spherical Shell

Abstract

The spherical shell and spherical zonal band are two elemental geometries that are often used as benchmarks for gravity field modeling. When applying the spherical shell and spherical zonal band discretized into tesseroids, the errors may be reduced or cancelled for the superposition of the tesseroids due to the spherical symmetry of the spherical shell and spherical zonal band. In previous studies, this superposition error elimination effect (SEEE) of the spherical shell and spherical zonal band has not been taken seriously, and it needs to be investigated carefully. In this contribution, the analytical formulas of the signal of derivatives of the gravitational potential up to third order (e.g., V, $V_{z}$, $V_{zz}$, $V_{xx}$, $V_{yy}$, $V_{zzz}$, $V_{xxz}$, and $V_{yyz}$) of a tesseroid are derived when the computation point is situated on the polar axis. In comparison with prior research, simpler analytical expressions of the gravitational effects of a spherical zonal band are derived from these novel expressions of a tesseroid. In the numerical experiments, the relative errors of the gravitational effects of the individual tesseroid are compared to those of the spherical zonal band and spherical shell not only with different 3D Gauss–Legendre quadrature orders ranging from (1,1,1) to (7,7,7) but also with different grid sizes (i.e., $5^{\circ }\times 5^{\circ }$, $2^{\circ }\times 2^{\circ }$, $1^{\circ }\times 1^{\circ }$, $30^{\prime }\times 30^{\prime }$, and $15^{\prime }\times 15^{\prime }$) at a satellite altitude of 260 km. Numerical results reveal that the SEEE does not occur for the gravitational components V, $V_{z}$, $V_{zz}$, and $V_{zzz}$ of a spherical zonal band discretized into tesseroids. The SEEE can be found for the $V_{xx}$ and $V_{yy}$, whereas the superposition error effect exists for the $V_{xxz}$ and $V_{yyz}$ of a spherical zonal band discretized into tesseroids on the overall average. In most instances, the SEEE occurs for a spherical shell discretized into tesseroids. In summary, numerical experiments demonstrate the existence of the SEEE of a spherical zonal band and a spherical shell, and the analytical solutions for a tesseroid can benefit the investigation of the SEEE. The single tesseroid benchmark can be proposed in comparison to the spherical shell and spherical zonal band benchmarks in gravity field modeling based on these new analytical formulas of a tesseroid.

Article Highlights

• The comprehensive study of the spherical shell and spherical zonal band discretized into tesseroids is reviewed

• The analytical expressions for the signal of derivatives of the gravitational potential up to the third order of a tesseroid and a spherical zonal band are derived when the computation point is located on the polar axis

• The superposition error elimination effect of the spherical shell and spherical zonal band discretized into tesseroids is numerically confirmed

1 Introduction

In gravity field modeling, spherical shells are frequently employed as a benchmarking tool (Root et al. 2022). Generally, a spherical shell is the difference between two concentric spheres with different radii. A spherical shell can serve as the benchmark for different types of mass bodies, e.g., global spherical harmonics, tesseroid, triangle, and hexahedral integrations (Root et al. 2022). The reason is that the gravitational effects of a spherical shell have analytical solutions and they can be treated as reference values compared to the computed values from discretizations with different mass bodies in a variety of numerical experiments. In prior research, the analytical formulas of a spherical shell were derived for the gravitational effects, e.g., gravitational potential (GP) (MacMillan 1930; Blakely 1995; Tsoulis 1999; Heck and Seitz 2007; Makhloof and Ilk 2008; Torge and Müller 2012; Grombein et al. 2013; Shen and Deng 2016; Uieda et al. 2016; Fukushima 2018; Soler et al. 2019; Lin and Denker 2019; Qiu and Chen 2020; Lin et al. 2020; Karcol 2011, 2021; Ouyang et al. 2022), gravity vector (GV, first-order derivatives of the GP) or gravitational attraction (MacMillan 1930; Blakely 1995; Tsoulis 1999; Heck and Seitz 2007; Makhloof and Ilk 2008; Grombein et al. 2013; Uieda et al. 2016; Marotta and Barzaghi 2017; Fukushima 2018; Soler et al. 2019; Lin and Denker 2019; Qiu and Chen 2020; Lin et al. 2020; Karcol 2011, 2021; Deng 2022; Root et al. 2022; Ouyang et al. 2022), gravity gradient tensor (GGT, second-order derivatives of the GP) (Makhloof and Ilk 2008; Grombein et al. 2013; Uieda et al. 2016; Fukushima 2018; Lin et al. 2020; Qiu and Chen 2020; Deng 2022; Ouyang et al. 2022), gravitational curvatures (GC, third-order derivatives of the GP) (Deng and Shen 2018a, b, 2019; Deng 2022), certain nth-order derivatives of the GP (Deng et al. 2020), and first-order derivatives of the invariants of the gravity gradient tensor (Deng et al. 2021). Note that the orders of differentiation for the GP, GV, GGT, and GC are 0, 1, 2, and 3.

Among several schemes for a spherical shell benchmark, a discretization using tesseroids has been a common strategy to investigate the numerical performance of the algorithms to compute the tesseroid’s gravitational and magnetic effects in the gravity and magnetic fields. A whole spherical shell can be discretized into tesseroids along the coordinate lines, i.e., in longitude, latitude (or colatitude), and radial directions. The relative errors between the analytical gravitational or magnetic effects and the sum of the calculated gravitational or magnetic effects of the discretized tesseroids forming the entire spherical shell are investigated by using different numerical approaches, e.g., Taylor series expansion with different orders (Grombein et al. 2013; Shen and Deng 2016; Deng and Shen 2018a, b), Taylor series expansion and kernel matrix equivalence method (Zeng et al. 2022), 3D or 2D Gauss-Legendre quadrature (GLQ) (Deng and Shen 2018b; Zhong et al. 2019; Deng et al. 2020, 2022), 3D or 2D adaptive discretization stack-based GLQ approach (Uieda et al. 2016; Baykiev et al. 2016; Deng and Shen 2019; Lin and Denker 2019), conditional split and double exponential quadrature method (Fukushima 2018), 2D density-based adaptive discretization GLQ method (Soler et al. 2019), variable-order GLQ approach (Qiu and Chen 2020), combination of Taylor series expansion and GLQ method (Lin et al. 2020), and combination of GLQ method with 2D adaptive discretization and discrete convolution algorithm based on 1D fast Fourier transform (Ouyang et al. 2022). Note that most of the above-mentioned studies focused on global errors of a whole spherical shell rather than the local errors of the tesseroid for this commonly used strategy.

Moreover, the spherical zonal band has often been used in the literature as a geometrical element to test and validate (or to benchmark) gravity field modeling algorithms. In general, a spherical zonal band is the difference between two concentric spherical caps with different spherical distances $\psi _{i}$ and $\psi _{i+1}$ (Deng 2022), which is a volumetric element. A spherical zonal band is a component of a spherical shell, i.e., it becomes a spherical shell when its first spherical latitude equals zero and its second spherical latitude equals $\pi$. When the computation point is positioned on the polar axis, the analytical expressions for a spherical zonal band can be derived for the gravitational effects, e.g., GP (Heck and Seitz 2007; Yang et al. 2022), GV (Heck and Seitz 2007; Lin and Denker 2019; Deng 2022), GGT (Lin et al. 2020; Deng 2022), and GC (Deng 2022).

Analogously, a spherical zonal band can be discretized into tesseroids with respect to the longitude and radial coordinates. In other words, a tesseroid can be treated as a sector of a spherical zonal band. Recently, it was numerically confirmed that the computation efficiency of this strategy was higher and its computation errors were smaller than those of a spherical shell discretized using tesseroid (Deng 2022). The main reason is that the shell consists of many zonal bands. This strategy can also be applied to investigate the performance of different numerical methods for calculating the gravitational effects of the tesseroid, e.g., Taylor series expansion (Heck and Seitz 2007; Wild-Pfeiffer 2008; Lin and Denker 2019; Yang et al. 2022) and GLQ (Wild-Pfeiffer 2008; Lin and Denker 2019; Deng 2022) approaches. Generally, in previous numerical experiments, the global errors of the total spherical zonal band were also evaluated rather than the local errors of the tesseroid.

The strategies of a spherical zonal band and spherical shell discretized into tesseroids effectively calculate the global errors of the gravitational effects of the total spherical zonal band and spherical shell. The numerical results from the two strategies have constraints when employing the tesseroid with different numerical methods in practical applications. In particular, the numerical results of the error analysis from the aforementioned different numerical approaches by using the strategies of the spherical zonal band and spherical shell discretized into tesseroids can only be applied to global situations in the discretized tesseroids forming the entire spherical zonal band and spherical shell (Heck and Seitz 2007; Wild-Pfeiffer 2008; Grombein et al. 2013; Shen and Deng 2016; Uieda et al. 2016; Baykiev et al. 2016; Fukushima 2018; Deng and Shen 2018a, b, 2019; Zhong et al. 2019; Lin and Denker 2019; Soler et al. 2019; Lin et al. 2020; Qiu and Chen 2020; Deng et al. 2020, 2022; Zeng et al. 2022; Yang et al. 2022; Deng 2022; Ouyang et al. 2022). However, for local practical calculations, the numerical results from these global error assessments do not apply. For example, in Section ‘Evaluation of the accuracy’ of Uieda et al. (2016), the spherical shell was adopted to evaluate the computation accuracy of the GP, GV, and GGT of the discretized tesseroids that comprise the entire spherical shell. The threshold error 0.1% was only for the global error assessments of the whole spherical shell. When using the tesseroids with the algorithm in Uieda et al. (2016) for local practical calculations, the conclusion derived from this global threshold error 0.1% cannot be applied. It should be re-evaluated for the specific local error assessments. Usually, they tend to underestimate error levels due to the superposition error elimination effect (SEEE) (Deng et al. 2022). The definition of the SEEE is the possibility that the symmetry of the global spherical shell with the discretized tesseroids might cancel out some errors from individual tesseroids (Deng et al. 2022). This SEEE was not noticed in the previous works. Careful investigation of the SEEE will help to make better use of tesseroids in the practical applications of gravity field modeling. In reality, the spherical zonal band may also have the SEEE. The SEEE is merely a hypothesis proposed in Deng et al. (2022) that has not yet been validated by numerical experiments. Concerning the spherical zonal band and spherical shell discretized into tesseroids, it is necessary to analyze the SEEE by comparing the global errors of the spherical zonal band and spherical shell with the local errors of the individual tesseroid. Consequently, it is vital to examine the variation in the local errors of the individual tesseroid in detail.

The challenge of evaluating the local errors of an individual tesseroid is to derive analytical expressions for the gravitational effects of a tesseroid. This is difficult because since the concept of the tesseroid was proposed in Anderson (1976), subsequent studies have used different numerical methods to calculate the gravitational effects of a tesseroid (Kuhn 2003; Heck and Seitz 2007; Asgharzadeh et al. 2007; Wild-Pfeiffer 2008; Tsoulis et al. 2009; Grombein et al. 2013; Shen and Deng 2016; Uieda et al. 2016; Deng and Shen 2018b; Zhao et al. 2019; Soler et al. 2019; Lin et al. 2020; Zeng et al. 2022; Ouyang et al. 2022). The primary reason is that in the general formulas of the gravitational effects of a tesseroid, the double integrals of the longitude and colatitude (or latitude) coordinates were considered incapable of analytical integration in previous studies. However, some research progress has brought a turning point to this challenge and provided the research idea for the solution of this difficult problem. For example, the gravitational effects of a spherical zonal band can be solved analytically if the computation point is located on the polar axis (Heck and Seitz 2007; Marotta and Barzaghi 2017; Lin and Denker 2019; Deng 2022). Marotta and Barzaghi (2017) derived the analytical gravitational acceleration of a tesseroid when the computation point is located on the polar axis based on Sect. 5.2 of Turcotte and Schubert (2002), see also Lin and Li (2022). Thus, the key idea is the special condition of the computation point located on the polar axis.

This paper goes beyond the previous studies in that the analytical formulas of the gravitational effects including the GP, GV, GGT, and GC of a tesseroid are derived when the computation point is located on the polar axis. The formulas of the gravitational effects of a spherical zonal band are also analytically derived. These new formulas of the gravitational effects of a spherical zonal band are simpler in forms and more intuitive in methods than those in Deng (2022). Moreover, the relative errors of the gravitational effects of a single tesseroid are obtained to investigate the SEEE of the spherical zonal band and spherical shell discretized into tesseroids.

The paper is organized as follows. Section 2 offers the theoretical aspects of this paper, in which the analytical formulas of the GP, GV, GGT, and GC of a tesseroid are derived in Sects. 2.1, 2.2, 2.3, and 2.4, respectively. Sections 2.5 and 2.6 derive the analytical formulas of these gravitational effects of a spherical zonal band and spherical shell, respectively. Numerical experiments are performed in Sect. 3, in which Sect. 3.1 presents the basic setup. The influences of the 3D Gauss-Legendre quadrature orders and grid sizes on the gravitational effects of the tesseroid, spherical zonal band, and spherical shell are investigated in Sects. 3.2 and 3.3, respectively. Section 3.4 compares the gravitational effects of every individual tesseroid forming the whole spherical zonal band and spherical shell. Finally, the main conclusions and outlook for future studies are summarized in Sect. 4.

2 Theoretical Aspects

2.1 Analytical Formula of the GP of a Tesseroid

Fig. 1

Illustration of a tesseroid in the spherical coordinate system revised from Fig. 3.8 of Anderson (1976). $\Delta \lambda =\lambda _2-\lambda _1$, $\Delta \theta =\theta _2-\theta _1$ (or $\Delta \varphi =\varphi _2-\varphi _1$), and $\Delta r = r_2-r_1$ are the longitude, colatitude (or latitude), and radial dimensions of the tesseroid, in which $\Delta \theta = \Delta \varphi$. $P(\lambda ,\theta ,r)$ (or $P(\lambda ,\varphi ,r)$) and $Q(\lambda ^{\prime },\theta ^{\prime },r^{\prime })$ (or $Q(\lambda ^{\prime },\varphi ^{\prime },r^{\prime })$) are the computation and integration points, respectively. There is the relation between the colatitude $\theta$ (or $\theta ^{\prime }$) and latitude $\varphi$ (or $\varphi ^{\prime }$) of the computation point P (or integration point Q) as $\theta + \varphi = 90^{\circ }$ (or $\theta ^{\prime } + \varphi ^{\prime } = 90^{\circ }$). P(x, y, z) is in the local north-oriented frame system, where x, y, and z point to the north, east, and radial up directions, respectively

A tesseroid (see Fig. 1) is the mass body in the spherical or ellipsoidal coordinate system defined by three pairs of longitudes, colatitudes (or latitudes), and radial distances (Anderson 1976). In previous studies (Kuhn 2003; Heck and Seitz 2007; Asgharzadeh et al. 2007; Wild-Pfeiffer 2008; Grombein et al. 2013; Shen and Deng 2016; Uieda et al. 2016; Deng and Shen 2018a, b, 2019), the gravitational effects of a tesseroid were often calculated numerically because the integrals with respect to the longitude and colatitude (or latitude) in their expressions are not considered to be integrated analytically. In this section, the analytical formula of the GP of a tesseroid is derived when the computation point is located on the polar axis.

Generally, the formula of the GP (V) of a tesseroid is expressed in the spherical coordinate system as (Anderson 1976; Blakely 1995; Kuhn 2003; Heck and Seitz 2007; Asgharzadeh et al. 2007; Wild-Pfeiffer 2008; Shen and Deng 2016; Uieda et al. 2016; Deng and Shen 2019):

$$\begin{aligned} V(\lambda , \theta , r)=\, & {} G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{\theta _{1}}^{\theta _{2}} \frac{{r^{\prime }}^{2}}{l} \sin \theta ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \end{aligned}$$

(1)

$$\begin{aligned} l= & {} \sqrt{r^{2}+r^{\prime 2}- 2 r r^{\prime } \cos \psi } \end{aligned}$$

(2)

$$\begin{aligned} \cos \psi= & {} \cos \theta \cos \theta ^{\prime } + \sin \theta \sin \theta ^{\prime } \cos (\lambda ^{\prime }-\lambda ) \end{aligned}$$

(3)

where G is the gravitational constant, $\rho$ is the constant density of a homogeneous tesseroid, and l is the Euclidean distance between the computation point $P(\lambda , \theta , r)$ and integration point $Q(\lambda ^{\prime }, \theta ^{\prime }, r^{\prime })$ with their longitudes ($\lambda$ and $\lambda ^{\prime }$), colatitudes ($\theta$ and $\theta ^{\prime }$), and geocentric distances (r and $r^{\prime }$). [$\lambda _1$, $\lambda _2$], [$\theta _1$, $\theta _2$], and [$r_1$, $r_2$] are the longitude, colatitude, and radial boundaries of a tesseroid, i.e., the integration boundaries of the tesseroid are $\lambda ^{\prime } = [\lambda _1, \lambda _2]$, $\theta ^{\prime } = [\theta _1, \theta _2]$, and $r^{\prime } = [r_1, r_2]$.

When the computation point P is located on the polar axis, the colatitude of the computation point P is $\theta$ = 0 or $\theta$ = $\pi$. To simplify the derivation process, $\theta = 0$ is adopted as the example for the situation of the computation point located on the polar axis. The derivation progress with $\theta = \pi$ is similar to that of $\theta$ = 0 and there are small changes in the solution for $\theta = \pi$. Under this circumstance, the expression for the GP of a tesseroid with the triple integral form in Eq. (1) has the analytical solution. The detailed derivation is presented in Appendix A. The analytical formula of the GP of a tesseroid when the computation point is located on the positive part of the polar axis (i.e., $\theta$ = 0) is obtained as:

$$\begin{aligned} \begin{aligned} V =&\frac{G \rho (\lambda _2 - \lambda _1)}{12 r} \Big [ A_{22} l_{22} - A_{12} l_{12} - A_{21} l_{21} + A_{11} l_{11} \\&+ 6 B_{2} \ln \Big ( \frac{C_{22} + l_{22}}{C_{12} + l_{12}} \Big ) + 6 B_{1} \ln \Big ( \frac{C_{11} + l_{11}}{C_{21} + l_{21}} \Big ) \Big ] \end{aligned} \end{aligned}$$

(4)

where the expressions for the $A_{22}$, $A_{12}$, $A_{21}$, $A_{11}$, $B_{2}$, $B_{1}$, $C_{22}$, $C_{12}$, $C_{21}$, $C_{11}$, $l_{22}$, $l_{12}$, $l_{21}$, and $l_{11}$ are listed in Table 8 in Appendix A. Note that the presented formula in Eq. (4) is singular for the $r = 0$, see the more general solution in Karcol (2021).

2.2 Analytical Formula of the GV of a Tesseroid

Differentiating Eq. (1) with respect to the geocentric distance r of the computation point P, the formula of the radial GV of a tesseroid is presented as (Heck and Seitz 2007; Asgharzadeh et al. 2007; Uieda et al. 2016; Deng and Shen 2019):

$$\begin{aligned} {V_{r} (\lambda , \theta , r)}=\, & {} \frac{\partial V(\lambda , \theta , r)}{\partial r} \nonumber \\=\, & {} G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{\theta _{1}}^{\theta _{2}} {r^{\prime }}^{2} \frac{\Delta _z}{l^{3}} \sin \theta ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \end{aligned}$$

(5)

$$\begin{aligned} \Delta _z=\, & {} r^{\prime } \cos \psi - r \end{aligned}$$

(6)

Similarly, when the computation point is located on the polar axis, there exists the analytical solution for Eq. (5). The analytical expression for the GV (i.e., $V_r$, $V_x$, and $V_y$) of a tesseroid is derived in Appendix B. The analytical solution for the radial GV of a tesseroid with the colatitude of the computation point $\theta =0$ is obtained as:

$$\begin{aligned} \begin{aligned} { V_{r}} =&- \frac{G \rho (\lambda _2 - \lambda _1)}{3 r^2} \Big [ D_{22} l_{22} - D_{12} l_{12} - D_{21} l_{21} + D_{11} l_{11} \\&+ 3 B_{2} \ln \Big ( \frac{C_{12} + l_{12}}{C_{22} + l_{22}} \Big ) + 3 B_{1} \ln \Big ( \frac{C_{21} + l_{21}}{C_{11} + l_{11}} \Big ) \Big ] \end{aligned} \end{aligned}$$

(7)

where the expressions for the $B_{2}$, $B_{1}$, $C_{22}$, $C_{12}$, $C_{21}$, $C_{11}$, $l_{22}$, $l_{12}$, $l_{21}$, and $l_{11}$ are referred to in Table 8 and the expressions for the $D_{22}$, $D_{12}$, $D_{21}$, and $D_{11}$ are listed in Table 9 in Appendix B.

Note that Marotta and Barzaghi (2017) derived the analytical formula of the gravitational acceleration $\Delta g_{P}$ in Appendix 2 when the computation point is located on the polar axis based on Sect. 5.2 of Turcotte and Schubert (2002). The differences between the $V_{r}$ in Eq. (7) in this paper and $\Delta g_{P}$ in Eq. (2) of Marotta and Barzaghi (2017) lie in that: (1) the usage of the $r_{2}$, $r_{1}$, $\theta _{2}$, and $\theta _{1}$ in this paper corresponds to that of the $R+h$, R, ${\theta ^{\prime }}_{2}$, and ${\theta ^{\prime }}_{1}$ in Marotta and Barzaghi (2017); and (2) the $\Delta g_{P}$ adds the minus symbol (i.e., −), whereas the $V_{r}$ has no minus symbol. Despite these differences, the formula of the $V_{r}$ in Eq. (7) of this paper is the same as that of $\Delta g_{P}$ in Marotta and Barzaghi (2017) after the parameter exchange and absolute operation.

2.3 Analytical Formulas of the GGT of a Tesseroid

Differentiating Eq. (1) with respect to the geocentric distance r of the computation point twice, the formula of the radial–radial GGT of a tesseroid is obtained as (Asgharzadeh et al. 2007; Grombein et al. 2013; Uieda et al. 2016; Deng and Shen 2019):

$$\begin{aligned} \begin{aligned} { V_{rr} (\lambda , \theta , r)}&= \frac{\partial ^2 V(\lambda , \theta , r)}{\partial r^2} \\&= G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{\theta _{1}}^{\theta _{2}} {r^{\prime }}^{2} \Big ( \frac{3 {\Delta _z}^2}{l^{5}} - \frac{1}{l^{3}} \Big ) \sin \theta ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(8)

Analogously, Eq. (8) has the analytical solution when the computation point is located on the polar axis. The derivation of the analytical solutions for the GGT of a tesseroid is presented in Appendix C. The analytical expression for the radial-radial GGT of a tesseroid with $\theta = 0$ is obtained as:

$$\begin{aligned} \begin{aligned} { V_{rr}} =&\frac{G \rho (\lambda _2 - \lambda _1)}{6 r^3} \Big [ \frac{E_{22}}{l_{22}} - \frac{E_{12}}{l_{12}} - \frac{E_{21}}{l_{21}} + \frac{E_{11}}{l_{11}} \\&+ 6 B_{2} \ln \Big ( \frac{C_{22} + l_{22}}{C_{12} + l_{12}} \Big ) + 6 B_{1} \ln \Big ( \frac{C_{11} + l_{11}}{C_{21} + l_{21}} \Big ) \Big ] \end{aligned} \end{aligned}$$

(9)

where the expressions for the $B_{2}$, $B_{1}$, $C_{22}$, $C_{12}$, $C_{21}$, $C_{11}$, $l_{22}$, $l_{12}$, $l_{21}$, and $l_{11}$ are referred to in Table 8 and the expressions for the $E_{22}$, $E_{12}$, $E_{21}$, and $E_{11}$ are listed in Table 10 in Appendix C. Due to the common usage in the previous works (Uieda et al. 2016; Lin and Denker 2019; Lin et al. 2020), $V_{rr}$ is denoted as $V_{zz}$ in the following part.

Regarding the other components of the GGT, the components $V_{xx}$ and $V_{yy}$ are chosen to derive their analytical expressions when the computation point is located on the polar axis, because these three components $V_{xx}$, $V_{yy}$, and $V_{zz}$ of the GGT satisfy Laplace’s equation as $V_{xx} + V_{yy} + V_{zz} = 0$ in theory. Laplace’s equation will be applied to confirm the correctness of the derived analytical expressions for the $V_{xx}$, $V_{yy}$, and $V_{zz}$ of a tesseroid.

The general formulas of the $V_{xx}$ and $V_{yy}$ of a tesseroid in Cartesian integral kernels are expressed as (Grombein et al. 2013; Uieda et al. 2016; Deng and Shen 2019):

$$\begin{aligned} V_{xx} (\lambda , \theta , r)=\, & {} G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{\theta _{1}}^{\theta _{2}} {r^{\prime }}^{2} \Big ( \frac{3 {\Delta _x}^2}{l^{5}} - \frac{1}{l^{3}} \Big ) \sin \theta ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \end{aligned}$$

(10)

$$\begin{aligned} \Delta _x=\, & {} r^{\prime } \big [ \sin \theta \cos \theta ^{\prime } - \cos \theta \sin \theta ^{\prime } \cos (\lambda ^{\prime } - \lambda ) \big ] \end{aligned}$$

(11)

$$\begin{aligned} V_{yy} (\lambda , \theta , r)= & {} G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{\theta _{1}}^{\theta _{2}} {r^{\prime }}^{2} \Big ( \frac{3 {\Delta _y}^2}{l^{5}} - \frac{1}{l^{3}} \Big )\sin \theta ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \end{aligned}$$

(12)

$$\begin{aligned} \Delta _{y}= & {} r^{\prime } \sin \theta ^{\prime } \sin (\lambda ^{\prime }-\lambda ) \end{aligned}$$

(13)

When the computation point is located on the polar axis, Eqs. (10) and (12) have the analytical solutions. The analytical expressions for the $V_{xx}$ and $V_{yy}$ are derived in Appendix C. The analytical expressions for the $V_{xx}$ and $V_{yy}$ with $\theta =0$ are obtained as:

$$\begin{aligned} \begin{aligned} V_{xx} =&\frac{G \rho }{48} \Big [ F_{2} \ln \Big ( \frac{l_{22} + C_{22}}{l_{12} + C_{12}} \Big ) + F_{1} \ln \Big (\frac{l_{11} + C_{11}}{l_{21} + C_{21}} \Big ) \\&+ \frac{H_{2} + I_{22} + J_{2} + K_{22}}{r^3 l_{22}} - \frac{H_{1} + I_{12} + J_{1} + K_{12}}{r^3 l_{12}} \\&- \frac{H_{2} + I_{21} + J_{2} + K_{21}}{r^3 l_{21}} + \frac{H_{1} + I_{11} + J_{1} + K_{11}}{r^3 l_{11}} \Big ] \end{aligned} \end{aligned}$$

(14)

$$\begin{aligned} \begin{aligned} V_{yy} =&\frac{G \rho }{48} \Big [ L_{2} \ln \Big ( \frac{l_{22} + C_{22}}{l_{12} + C_{12}} \Big ) + L_{1} \ln \Big (\frac{l_{11} + C_{11}}{l_{21} + C_{21}} \Big ) \\&+ \frac{H_{2} + M_{22} - J_{2} + N_{22}}{r^3 l_{22}} - \frac{H_{1} + M_{12} - J_{1} + N_{12}}{r^3 l_{12}} \\&- \frac{H_{2} + M_{21} - J_{2} + N_{21}}{r^3 l_{21}} + \frac{H_{1} + M_{11} - J_{1} + N_{11}}{r^3 l_{11}} \Big ] \end{aligned} \end{aligned}$$

(15)

where the expressions for the $C_{22}$, $C_{12}$, $C_{21}$, $C_{11}$, $l_{22}$, $l_{12}$, $l_{21}$, and $l_{11}$ are referred to in Table 8. The expressions for the $F_{2}$, $F_{1}$, $H_{2}$, $H_{1}$, $I_{22}$, $I_{12}$, $I_{21}$, $I_{11}$, $J_2$, $J_1$, $K_{22}$, $K_{12}$, $K_{21}$, and $K_{11}$ are listed in Table 11 in Appendix C. The expressions for the $L_{2}$, $L_{1}$, $M_{22}$, $M_{12}$, $M_{21}$, $M_{11}$, $N_{22}$, $N_{12}$, $N_{21}$, and $N_{11}$ are presented in Table 12 in Appendix C. The differences of the sign between $F_{2}$ and $L_{2}$; $F_{1}$ and $L_{1}$; $I_{22}$ and $M_{22}$; $I_{12}$ and $M_{12}$; $I_{21}$ and $M_{21}$; $I_{11}$ and $M_{11}$; $K_{22}$ and $N_{22}$; $K_{12}$ and $N_{12}$; $K_{21}$ and $N_{21}$; $K_{11}$ and $N_{11}$ should be noted.

2.4 Analytical Formulas of the GC of a Tesseroid

Differentiating Eq. (1) with respect to the geocentric distance r of the computation point at three times, the formula of the radial–radial–radial GC of a tesseroid is obtained as (Deng and Shen 2018a, b, 2019):

$$\begin{aligned} \begin{aligned} { V_{rrr} (\lambda , \theta , r)}&= \frac{\partial ^3 V(\lambda , \theta , r)}{\partial r^3} \\&= G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{\theta _{1}}^{\theta _{2}} {r^{\prime }}^{2} \Big ( \frac{15 {\Delta _z}^3}{l^{7}} - \frac{9 \Delta _z}{l^{5}} \Big ) \sin \theta ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(16)

Similarly, the analytical solution exists for Eq. (16) when the computation point is located on the polar axis. The derivation of the analytical solution for the GC of a tesseroid is presented in Appendix D. The analytical formula of the radial–radial–radial GC of a tesseroid with $\theta =0$ is obtained as:

$$\begin{aligned} \begin{aligned} { V_{rrr}} = - \frac{ G \rho (\lambda _2 - \lambda _1)}{2 r^4} \Big ( \frac{ O_{22} }{ {l_{22}}^{3}} - \frac{ O_{12} }{ {l_{12}}^{3}} - \frac{ O_{21} }{ {l_{21}}^{3}} + \frac{ O_{11} }{ {l_{11}}^{3}} \Big ) \end{aligned} \end{aligned}$$

(17)

where the expressions for the $O_{22}$, $O_{12}$, $O_{21}$, and $O_{11}$ are listed in Table 13 in Appendix D, and the expressions for the $l_{22}$, $l_{12}$, $l_{21}$ and $l_{11}$ are referred to in Table 8. Similarly, $V_{rrr}$ is represented as $V_{zzz}$ due to the common utilization in Deng and Shen (2018a, 2018b, 2019).

Analogously, these three components $V_{xxz}$, $V_{yyz}$, and $V_{zzz}$ of the GC satisfy Laplace’s equation as $V_{xxz} + V_{yyz} + V_{zzz} = 0$. Thus, the analytical expressions for the $V_{xxz}$ and $V_{yyz}$ of a tesseroid are derived when the computation point is located on the polar axis.

Generally, the expressions for the $V_{xxz}$ and $V_{yyz}$ of a tesseroid in Cartesian integral kernels are presented as (Deng and Shen 2018b, 2019):

$$\begin{aligned} \begin{aligned} V_{xxz} (\lambda , \theta , r) = G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{\theta _{1}}^{\theta _{2}} {r^{\prime }}^{2} \Big ( \frac{15 {\Delta _x}^2 \Delta _z }{l^{7}} - \frac{3 \Delta _z }{l^{5}} \Big ) \sin \theta ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(18)

$$\begin{aligned} \begin{aligned} V_{yyz} (\lambda , \theta , r) = G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{\theta _{1}}^{\theta _{2}} {r^{\prime }}^{2} \Big ( \frac{15 {\Delta _y}^2 \Delta _z }{l^{7}} - \frac{3 \Delta _z }{l^{5}} \Big ) \sin \theta ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(19)

When the colatitude of the computation point is $\theta = 0$, there exist the analytical solutions for Eqs. (18) and (19). The detailed derivation process of the analytical expressions for the $V_{xxz}$ and $V_{yyz}$ of a tesseroid is presented in Appendix D. The analytical expressions for the $V_{xxz}$ and $V_{yyz}$ with $\theta =0$ are obtained as:

$$\begin{aligned} \begin{aligned} V_{xxz}&= \frac{G \rho }{16 r^4} \Big [ \frac{P_{22} + Q_{22} + R_{22} + S_{22} + T_{2}}{ {l_{22}}^3 } \\&\quad - \frac{P_{12} + Q_{12} + R_{12} + S_{12} + T_{1}}{ {l_{12}}^3 } \\&\quad - \frac{P_{21} + Q_{21}+ R_{21} + S_{21} + T_{2}}{{l_{21}}^3 } \\&\quad + \frac{P_{11} + Q_{11} + R_{11} + S_{11} + T_{1}}{{l_{11}}^3 } \Big ] \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned} \begin{aligned} V_{yyz}&= \frac{G \rho }{16 r^4} \Big [ \frac{V_{22} - Q_{22} + W_{22} + S_{22} + T_{2}}{ {l_{22}}^3 } \\&- \frac{V_{12} - Q_{12} + W_{12} + S_{12} + T_{1} }{ {l_{12}}^3 } \\&- \frac{V_{21} - Q_{21} + W_{21} + S_{21} + T_{2}}{{l_{21}}^3 } \\&+ \frac{V_{11} - Q_{11} + W_{11} + S_{11} + T_{1}}{ {l_{11}}^3 } \Big ] \end{aligned} \end{aligned}$$

(21)

where the expressions for the $l_{22}$, $l_{12}$, $l_{21}$, and $l_{11}$ are referred to in Table 8, the expressions for the $P_{22}$, $P_{12}$, $P_{21}$, $P_{11}$, $Q_{22}$, $Q_{12}$, $Q_{21}$, $Q_{11}$, $R_{22}$, $R_{12}$, $R_{21}$, $R_{11}$, $S_{22}$, $S_{12}$, $S_{21}$, $S_{11}$, $T_{2}$, and $T_{1}$ are listed in Table 14 in Appendix D, and the expressions for the $V_{22}$, $V_{12}$, $V_{21}$, $V_{11}$, $W_{22}$, $W_{12}$, $W_{21}$, and $W_{11}$ are presented in Table 15 in Appendix D. Note that there are the differences of the sign between $P_{22}$ and $V_{22}$; $P_{12}$ and $V_{12}$; $P_{21}$ and $V_{21}$; $P_{11}$ and $V_{11}$; $R_{22}$ and $W_{22}$; $R_{12}$ and $W_{12}$; $R_{21}$ and $W_{21}$; $R_{11}$ and $W_{11}$.

Regarding these expressions in Eqs. (4), (7), (9), (14), (15), (17), (20), and (21), the situation $\theta =0$ is considered. Other situations $\theta =\pi$ and $r=0$ are not considered, which could be investigated based on the work of Karcol (2021).

2.5 Analytical Formulas of Gravitational Effects of a Spherical Zonal Band

Fig. 2

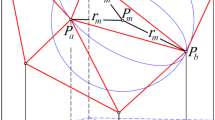
Visualization of a tesseroid (i.e., shadow part) and a spherical zonal band revised from Fig. 6 of Heck and Seitz (2007). The computation point $P (\lambda , \theta =0, r)$ is located on the polar axis. $Q (\lambda ^{\prime }, \theta ^{\prime }, r^{\prime })$ is the integrating point. O is the center of the sphere. $\Delta \lambda$, $\Delta \theta = \theta _2 - \theta _1$, and $\Delta r = r_2 - r_1$ are the longitude, colatitude, and radial dimensions of a tesseroid

Generally, a tesseroid can be treated as a sector of a spherical zonal band (see Fig. 2). In other words, when the longitude $\lambda ^{\prime }$ of the integration point Q integrates from $\lambda _{1}=0$ to $\lambda _{2}=2 \pi$ for a tesseroid, a spherical zonal band is obtained. In this study, the analytical solutions for the GP, GV, GGT, and GC of a spherical zonal band are derived based on these analytical expressions for a tesseroid.

Letting $\lambda _{1}=0$ and $\lambda _{2}=2 \pi$ in Eqs. (4), (7), (9), (14), (15), (17), (20) and (21), the analytical expressions for the GP ($V^{\textrm{zb}}$), radial GV (${V_{r}}^{\textrm{zb}}$), GGT (${V_{zz}}^{\textrm{zb}}$, ${V_{xx}}^{\textrm{zb}}$, and ${V_{yy}}^{\textrm{zb}}$), and GC (${V_{zzz}}^{\textrm{zb}}$, ${V_{xxz}}^{\textrm{zb}}$, and ${V_{yyz}}^{\textrm{zb}}$) of a spherical zonal band when the computation point is located on the positive part of the polar axis (i.e., $\theta =0$) are obtained as:

$$\begin{aligned} \begin{aligned} V^{\textrm{zb}} =&\frac{\pi G \rho }{6 r} \Big [ A_{22} l_{22} - A_{12} l_{12} - A_{21} l_{21} + A_{11} l_{11} \\&+ 6 B_{2} \ln \Big ( \frac{C_{22} + l_{22}}{C_{12} + l_{12}} \Big ) + 6 B_{1} \ln \Big ( \frac{C_{11} + l_{11}}{C_{21} + l_{21}} \Big ) \Big ] \end{aligned} \end{aligned}$$

(22)

$$\begin{aligned} \begin{aligned} { {V_{r}}^{\textrm{zb}} } =&- \frac{2 \pi G \rho }{3 r^2} \Big [ D_{22} l_{22} - D_{12} l_{12} - D_{21} l_{21} + D_{11} l_{11} \\&+ 3 B_{2} \ln \Big ( \frac{C_{12} + l_{12}}{C_{22} + l_{22}} \Big ) + 3 B_{1} \ln \Big ( \frac{C_{21} + l_{21}}{C_{11} + l_{11}} \Big ) \Big ] \end{aligned} \end{aligned}$$

(23)

$$\begin{aligned} \begin{aligned} {V_{zz}}^{\textrm{zb}} =&\frac{\pi G \rho }{3 r^3} \Big [ \frac{E_{22}}{l_{22}} - \frac{E_{12}}{l_{12}} - \frac{E_{21}}{l_{21}} + \frac{E_{11}}{l_{11}} \\&+ 6 B_{2} \ln \Big ( \frac{C_{22} + l_{22}}{C_{12} + l_{12}} \Big ) + 6 B_{1} \ln \Big ( \frac{C_{11} + l_{11}}{C_{21} + l_{21}} \Big ) \Big ] \end{aligned} \end{aligned}$$

(24)

$$\begin{aligned} \begin{aligned} {V_{xx}}^{\textrm{zb}}=\, &{V_{yy}}^{\textrm{zb}} \\=\, &- \frac{\pi G \rho }{6 r^3} \Big [ \frac{E_{22}}{l_{22}} - \frac{E_{12}}{l_{12}} - \frac{E_{21}}{l_{21}} + \frac{E_{11}}{l_{11}} \\&+ 6 B_{2} \ln \Big ( \frac{C_{22} + l_{22}}{C_{12} + l_{12}} \Big ) + 6 B_{1} \ln \Big ( \frac{C_{11} + l_{11}}{C_{21} + l_{21}} \Big ) \Big ] \end{aligned} \end{aligned}$$

(25)

$$\begin{aligned} \begin{aligned} {V_{zzz}}^{\textrm{zb}} = - \frac{ \pi G \rho }{r^4} \Big ( \frac{ O_{22} }{ {l_{22}}^{3}} - \frac{ O_{12} }{ {l_{12}}^{3}} - \frac{ O_{21} }{ {l_{21}}^{3}} + \frac{ O_{11} }{ {l_{11}}^{3}} \Big ) \end{aligned} \end{aligned}$$

(26)

$$\begin{aligned} \begin{aligned} {V_{xxz}}^{\textrm{zb}} =\, &{V_{yyz}}^{\textrm{zb}} \\ =\, &\frac{ \pi G \rho }{8 r^4} \Big [ \frac{X_{22} + Y_{22} + Z_{22}}{{l_{22}}^{3}} - \frac{X_{12} + Y_{12} + Z_{12}}{{l_{12}}^{3}} \\&- \frac{X_{21} + Y_{21} + Z_{21}}{{l_{21}}^{3}} + \frac{X_{11} + Y_{11} + Z_{11}}{{l_{11}}^{3}} \Big ] \end{aligned} \end{aligned}$$

(27)

where the expressions for the $A_{22}$, $A_{12}$, $A_{21}$, $A_{11}$, $B_{2}$, $B_{1}$, $C_{22}$, $C_{12}$, $C_{21}$, $C_{11}$, $l_{22}$, $l_{12}$, $l_{21}$, $l_{11}$, $D_{22}$, $D_{12}$, $D_{21}$, $D_{11}$, $E_{22}$, $E_{12}$, $E_{21}$, $E_{11}$, $O_{22}$, $O_{12}$, $O_{21}$, and $O_{11}$ are referred to in Tables 8, 9, 10, and 13. The expressions for the $X_{22}$, $X_{12}$, $X_{21}$, $X_{11}$, $Y_{22}$, $Y_{12}$, $Y_{21}$, $Y_{11}$, $Z_{22}$, $Z_{12}$, $Z_{21}$, and $Z_{11}$ are listed in Table 16 in Appendix E.

The other GV (${V_{x}}^{zb}$ and ${V_{y}}^{zb}$), GGT (${V_{xy}}^{zb}$, ${V_{xz}}^{zb}$, and ${V_{yz}}^{zb}$), and GC (${V_{xxx}}^{zb}$, ${V_{xxy}}^{zb}$, ${V_{xyz}}^{zb}$, ${V_{yyx}}^{zb}$, ${V_{yyy}}^{zb}$, ${V_{zzx}}^{zb}$, and ${V_{zzy}}^{zb}$) components of a spherical zonal band are the zero terms, i.e., ${V_{x}}^{zb}$ = ${V_{y}}^{zb}$ = 0, ${V_{xy}}^{zb}$ = ${V_{xz}}^{zb}$ = ${V_{yz}}^{zb}$ = 0, and ${V_{xxx}}^{zb}$ = ${V_{xxy}}^{zb}$ = ${V_{xyz}}^{zb}$ = ${V_{yyx}}^{zb}$ = ${V_{yyy}}^{zb}$ = ${V_{zzx}}^{zb}$ = ${V_{zzy}}^{zb}$ = 0. These behaviors can be confirmed in the Mathematica codes GV_VxVy.nb, GGT_VxyVxzVyz.nb, and GC_VxxxVxxyVxyzVyyxVyyyVzzxVzzy.nb at the link https://github.com/xiaoledeng/analytical-tesseroid-spherical-zonal-band.

In Appendix E, Laplace’s equation is applied to confirm the correctness of the derived analytical expressions for the GGT and GC of a tesseroid and spherical zonal band. The results reveal that these derived analytical expressions for a tesseroid and a spherical zonal band are correct.

In the previous studies, the formulas of the spherical zonal band were derived by the difference between two concentric spherical caps for the GP (${V}^{\textrm{zb}}$) (Papp and Wang 1996; Heck and Seitz 2007; Lin and Denker 2019), radial GV (${V_{r}}^{\textrm{zb}}$) (Heck and Seitz 2007; Lin and Denker 2019; Deng 2022), radial–radial GGT (${V_{zz}}^{\textrm{zb}}$) (Lin et al. 2020; Deng 2022), and radial–radial–radial GC (${V_{zzz}}^{\textrm{zb}}$) (Deng 2022). In theory, the numerical values of these previous formulas should be correspondingly equal to those of Eqs. (22), (23), (24), and (26), respectively. The consistency of the analytical expressions for the gravitational effects of a spherical zonal band between Deng (2022) and this paper is presented in Appendix F.

This study goes beyond the previous studies in that the analytical expressions for a spherical zonal band are efficiently obtained from the analytical formulas of a tesseroid by integrating the longitude of the integration point from 0 to $2 \pi$ when the colatitude of the computation point is $\theta = 0$. Meanwhile, the analytical expressions for the ${V_{xx}}^{\textrm{zb}}$, ${V_{yy}}^{\textrm{zb}}$, ${V_{xxz}}^{\textrm{zb}}$, and ${V_{yyz}}^{\textrm{zb}}$ are derived, in which ${V_{xx}}^{\textrm{zb}} = {V_{yy}}^{\textrm{zb}}$ and ${V_{xxz}}^{\textrm{zb}} = {V_{yyz}}^{\textrm{zb}}$.

2.6 Analytical Formulas of Gravitational Effects of a Spherical Shell

In general, a spherical shell can be discretized into tesseroids with respect to the longitude, colatitude (or latitude), and radial directions. When the longitude of the integration point $\lambda ^{\prime }$ integrates from $\lambda _{1}=0$ to $\lambda _{2}=2 \pi$ and its colatitude $\theta ^{\prime }$ integrates from $\theta _{1}=0$ to $\theta _{2}=\pi$ for a tesseroid, a spherical shell is obtained. In other words, a spherical shell can be treated as a hollow sphere. In this study, the analytical expressions for the GP, GV, GGT, and GC of a spherical shell are derived based on these analytical expressions for a tesseroid when the computation point is located on the polar axis.

Letting $\lambda _{1}=0$, $\lambda _{2}=2 \pi$, $\theta _{1}=0$, and $\theta _{2}=\pi$ in Eqs. (4), (7), (9), (14), (15), (17), (20) and (21), the analytical expressions for the GP ($V^{\textrm{sh}}$), GV (${V_{r}}^{\textrm{sh}}$), GGT (${V_{zz}}^{\textrm{sh}}$, ${V_{xx}}^{\textrm{sh}}$, and ${V_{yy}}^{\textrm{sh}}$), GC (${V_{zzz}}^{\textrm{sh}}$, ${V_{xxz}}^{\textrm{sh}}$, and ${V_{yyz}}^{\textrm{sh}}$) of a spherical shell with $\theta =0$ are obtained as:

$$\begin{aligned} V^{\textrm{sh}}= & {} \frac{4 \pi G \rho }{3r} ({r_{2}}^{3} - {r_{1}}^{3}) \end{aligned}$$

(28)

$$\begin{aligned} { {V_{r}}^{\textrm{sh}} }= & {} - \frac{4 \pi G \rho }{3 r^2} ({r_{2}}^{3} - {r_{1}}^{3}) \end{aligned}$$

(29)

$$\begin{aligned} {V_{zz}}^{\textrm{sh}}= & {} \frac{8 \pi G \rho }{3 r^3} ({r_{2}}^{3} - {r_{1}}^{3}) \end{aligned}$$

(30)

$$\begin{aligned} {V_{xx}}^{\textrm{sh}}= & {} {V_{yy}}^{\textrm{sh}} = - \frac{4 \pi G \rho }{3 r^3} ({r_{2}}^{3} - {r_{1}}^{3}) \end{aligned}$$

(31)

$$\begin{aligned} {V_{zzz}}^{\textrm{sh}}= & {} - \frac{8 \pi G \rho }{r^4} ({r_{2}}^{3} - {r_{1}}^{3}) \end{aligned}$$

(32)

$$\begin{aligned} {V_{xxz}}^{\textrm{sh}}= & {} {V_{yyz}}^{\textrm{sh}} = \frac{4 \pi G \rho }{r^4} ({r_{2}}^{3} - {r_{1}}^{3}) \end{aligned}$$

(33)

Note that these formulas in Eqs. (28)–(33) can be applied to a wider range for the computation point due to the symmetry of the spherical shell.

It is obvious that the expressions in Eqs. (28)–(33) are the same as the previous formulas of the spherical shell for the GP, radial GV (Tsoulis 1999; Vaníček et al. 2001, 2004; Heck and Seitz 2007; Makhloof and Ilk 2008; Grombein et al. 2013; Lin and Denker 2019; Lin et al. 2020), GGT (Makhloof and Ilk 2008; Lin et al. 2020), and GC (Deng and Shen 2018a, b, 2019). Meanwhile, the two pairs of the three components of the GGT and GC satisfy Laplace’s equation as ${V_{xx}}^{\textrm{sh}} + {V_{yy}}^{\textrm{sh}} + {V_{zz}}^{\textrm{sh}} = 0$ and ${V_{xxz}}^{\textrm{sh}} + {V_{yyz}}^{\textrm{sh}} + {V_{zzz}}^{\textrm{sh}} = 0$. Thus, the consistencies among these gravitational quantities of a spherical shell can be confirmed.

Analogously, regarding the other GV (${V_{x}}^{sh}$ and ${V_{y}}^{sh}$), GGT (${V_{xy}}^{sh}$, ${V_{xz}}^{sh}$, and ${V_{yz}}^{sh}$), and GC (${V_{xxx}}^{sh}$, ${V_{xxy}}^{sh}$, ${V_{xyz}}^{sh}$, ${V_{yyx}}^{sh}$, ${V_{yyy}}^{sh}$, ${V_{zzx}}^{sh}$, and ${V_{zzy}}^{sh}$) components of a spherical shell, ${V_{x}}^{sh}$ = ${V_{y}}^{sh}$ = 0, ${V_{xy}}^{sh}$ = ${V_{xz}}^{sh}$ = ${V_{yz}}^{sh}$ = 0, and ${V_{xxx}}^{sh}$ = ${V_{xxy}}^{sh}$ = ${V_{xyz}}^{sh}$ = ${V_{yyx}}^{sh}$ = ${V_{yyy}}^{sh}$ = ${V_{zzx}}^{sh}$ = ${V_{zzy}}^{sh}$ = 0. These components are the zero terms. The Mathematica codes GV_VxVy.nb, GGT_VxyVxzVyz.nb, and GC_VxxxVxxyVxyzVyyxVyyyVzzxVzzy.nb at the link https://github.com/xiaoledeng/analytical-tesseroid-spherical-zonal-band can demonstrate these characteristics.

3 Numerical Investigations

3.1 Setup of the Numerical Experiments

In the following numerical experiments, the basic numerical strategy is to compare the relative errors between the calculated values and the reference values of the gravitational effects. The difference from previous studies is that this paper investigates the relative errors between the calculated values and reference values of the gravitational effects of a single tesseroid, which helps to understand the superposition error (or elimination) effect of a spherical zonal band and spherical discretized into tesseroids. By using tesseroids to discretize a spherical zonal band and a spherical shell, there are no relative errors for the zero terms of the GV, GGT, and GC components ($V_{x}$, $V_{y}$, $V_{xy}$, $V_{xz}$, $V_{yz}$, $V_{xxx}$, $V_{xxy}$, $V_{xyz}$, $V_{yyx}$, $V_{yyy}$, $V_{zzx}$, and $V_{zzy}$) in the numerical experiments. Thus, these zero terms are not considered in the following experiments.

The general formula of the relative errors in $\log _{10}$ scale of the gravitational effects is presented as:

$$\begin{aligned} \delta F = \log _{10} \left( \left| \frac{F^{\textrm{cal}}}{F^{\textrm{ref}}} -1 \right| \right) \end{aligned}$$

(34)

where $\delta F$ means the relative errors in $\log _{10}$ scale of the gravitational effects ($\delta V$, $\delta V_{r}$, $\delta V_{zz}$, $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{zzz}$, $\delta V_{xxz}$, and $\delta V_{yyz}$) of the tesseroid, spherical zonal band, and spherical shell. $F^{\textrm{ref}}$ represents the reference values of the gravitational effects of the tesseroid, spherical zonal band, and spherical shell. $F^{\textrm{cal}}$ denotes the calculated values of the gravitational effects not only for a single tesseroid but also for the sum of every individual tesseroids forming the whole spherical zonal band and spherical shell.

Based on the analytical expressions for the GP (V), GV ($V_{r}$), GGT ($V_{zz}$, $V_{xx}$, and $V_{yy}$), and GC ($V_{zzz}$, $V_{xxz}$, and $V_{yyz}$) of a tesseroid in Eqs. (4), (7), (9), (14), (15), (17), (20), and (21), the reference values of the gravitational effects of the tesseroid are obtained. Analogously, the reference values of the gravitational effects of the spherical zonal band and spherical shell are calculated by Eqs. (22)–(27) and Eqs. (28)–(33), respectively.

Table 1 Detailed expressions for the GP (V), GV ($V_{r}$), GGT ($V_{zz}$, $V_{xx}$, and $V_{yy}$), and GC ($V_{zzz}$, $V_{xxz}$, and $V_{yyz}$) of a tesseroid in Cartesian integral kernels with the computation point located on the polar axis, where $l =\sqrt{r^2 + {r^{\prime }}^2 -2r r^{\prime } \sin \varphi ^{\prime } }$, $\Delta _x=- r^{\prime } \cos \varphi ^{\prime } \cos (\lambda ^{\prime }-\lambda )$, $\Delta _y=r^{\prime } \cos \varphi ^{\prime } \sin (\lambda ^{\prime }-\lambda )$, $\Delta _z=r^{\prime } \sin \varphi ^{\prime } -r$, and $\kappa ={r^{\prime }}^{2} \cos \varphi ^{\prime }$

To make the process of the calculated gravitational effects of the tesseroid complete, the expressions for the GP, GV, GGT, and GC of a tesseroid in Cartesian integral kernels are listed in Table 1, which are cited from Appendix 1 of Deng and Shen (2019). In this paper, the calculated values of the gravitational effects of the tesseroid in Table 1 are obtained by using the 3D GLQ approach. The GLQ is a commonly used numerical method to calculate the integrals in the expressions for the gravitational and magnetic effects of a tesseroid in previous studies (Ku 1977; Blakely 1995; Asgharzadeh et al. 2007, 2008, 2018; Wild-Pfeiffer 2008; Hirt et al. 2011; Li et al. 2011; Hinze et al. 2013; Du et al. 2015; Rexer and Hirt 2015; Roussel et al. 2015; Uieda et al. 2016; Baykiev et al. 2016; Deng and Shen 2018b, 2019; Soler et al. 2019; Zhao et al. 2019; Zhong et al. 2019; Lin and Denker 2019; Lin et al. 2020; Qiu and Chen 2020, 2021; Deng et al. 2020, 2022). The general formula of the 3D GLQ to compute the GP, GV, GGT, and GC of the tesseroid is presented as (Wild-Pfeiffer 2008; Hirt et al. 2011; Hinze et al. 2013; Uieda et al. 2016; Deng and Shen 2018b):

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} \int _{\varphi _{1}}^{\varphi _{2}} \int _{\lambda _{1}}^{\lambda _{2}} f\left( \lambda ^{\prime }, \varphi ^{\prime }, r^{\prime }\right) d \lambda ^{\prime } d \varphi ^{\prime } d r^{\prime } \\&\approx \frac{\left( \lambda _{2}-\lambda _{1}\right) \left( \varphi _{2}-\varphi _{1}\right) \left( r_{2}-r_{1}\right) }{8} \sum _{i=1}^{N^{\lambda }} \sum _{j=1}^{N^{\varphi }} \sum _{k=1}^{N^{r}} W_{i}^{\lambda } W_{j}^{\varphi } W_{k}^{r} f\left( \lambda _{i}, \varphi _{j}, r_{k}\right) \end{aligned} \end{aligned}$$

(35)

where $f\left( \lambda ^{\prime }, \varphi ^{\prime }, r^{\prime }\right)$ means the Cartesian integral kernels of the GP, GV, GGT, and GC in Table 1. $W_{i}^{\lambda }$, $W_{j}^{\varphi }$, and $W_{k}^{r}$ are the weights and $N^{\lambda }$, $N^{\varphi }$, and $N^{r}$ are the integer orders for the spherical longitude, latitude, and geocentric distance, respectively. $f\left( \lambda _{i}, \varphi _{j}, r_{k}\right)$ denotes the integral kernels of the GP, GV, GGT, and GC with the point $\left( \lambda _{i}, \varphi _{j}, r_{k}\right)$. The detailed formulas of the $W_{i}^{\lambda }$, $W_{j}^{\varphi }$, $W_{k}^{r}$, $\lambda _{i}$, $\varphi _{j}$, and $r_{k}$ can be referred to in Eqs. (23) – (28) and Table 5 of Deng and Shen (2018b).

Table 2 Numerical values of the parameters in numerical experiments

The numerical values of the parameters for the computation point, tesseroid, spherical zonal band, and spherical shell are listed in Table 2. It should be noted that the values of the $r_2$ and $r_1$ for the tesseroid in Table 2 also apply for the spherical zonal band and spherical shell. Regarding the calculated values of the gravitational effects of the tesseroid, the latitudes (i.e., $\varphi$, $\varphi ^{\prime }$, $\varphi _1$, and $\varphi _2$) are applied, whereas the colatitudes (i.e., $\theta$, $\theta ^{\prime }$, $\theta _1$, and $\theta _2$) are adopted to compute the reference values of the gravitational effects of the tesseroid, spherical zonal band, and spherical shell. The height of the computation point is the GOCE-type satellite height 260 km (Grombein et al. 2013; Uieda et al. 2016; Deng and Shen 2018a, b), which can largely reduce the near-zone problem (Deng and Shen 2018a, b; Deng et al. 2021; Deng 2022), i.e., large relative errors occur when the computation point approaches the near surface of the mass body.

3.2 Influence of GLQ Orders on Gravitational Effects of the Tesseroid, Spherical Zonal Band, and Spherical Shell

The chosen orders of the GLQ are important to the accuracy of the calculated gravitational effects of a tesseroid. In previous studies, the computation errors generally reduced with the increased orders of the GLQ, and the determination of the truncated GLQ orders was based on the computation accuracy of the numerical strategy with a spherical shell discretized into tesseroids, e.g., Uieda et al. (2016), Deng and Shen (2018b, 2019), Soler et al. (2019), Zhao et al. (2019), and Deng et al. (2020). Different from the previous studies, a spherical zonal band discretized into tesseroids is adopted in this section to investigate the influence of the 3D GLQ orders on the GP, GV, GGT, and GC of the tesseroids. Moreover, the relative errors of the gravitational effects of a single tesseroid between the calculated values and reference values are also studied. Note that the term ‘nodes’ of the GLQ in Deng and Shen (2018b) and Deng et al. (2020, 2022) should be replaced by the ‘degrees’ or ‘orders’.

The numerical values of the basic parameters are referred to in Table 2. The computation point P is located on the polar axis with its longitude $\lambda =0^{\circ }$, colatitude $\theta =0^{\circ }$ (or latitude $\varphi =90^{\circ }$), and geocentric distance $r=6,638,137$ m, which is 260 km above the surface of the spherical shell. The colatitudes of the spherical zonal band are $\theta _1 = 10^{\circ }$ and $\theta _2 = 11^{\circ }$. In other words, the grid size of the discretized tesseroids is $1^{\circ }\times 1^{\circ }$ not only for the spherical zonal band but also for the spherical shell. To calculate the reference values of the gravitational effects of a single tesseroid, the first tesseroid within the spherical zonal band is chosen, i.e., the colatitude boundaries of this single tesseroid are the same as those of the spherical zonal band as $\theta _1 = 10^{\circ }$ and $\theta _2 = 11^{\circ }$ and its longitude boundaries are $\lambda _1=0^{\circ }$ and $\lambda _2=1^{\circ }$. Regarding the calculated values of the gravitational effects of this single tesseroid, its latitude boundaries are $\varphi _1=90^{\circ }-\lambda _2=79^{\circ }$ and $\varphi _2=90^{\circ }-\lambda _1=80^{\circ }$ and longitude boundaries are $\lambda _1=0^{\circ }$ and $\lambda _2=1^{\circ }$.

By using Eq. (34) for the single tesseroid, spherical zonal band, and spherical shell, their relative errors of the gravitational effects in $\log _{10}$ scale with different 3D GLQ orders from (1, 1, 1) to (7, 7, 7) are illustrated in Fig. 3. In addition, the values of these relative errors are listed in Table 3.

Fig. 3

Illustration of the relative errors of the gravitational effects in $\log _{10}$ scale for (a) a single tesseroid, (b) a spherical zonal band, and (c) a spherical shell with the influence of the 3D GLQ orders from (1, 1, 1) to (7, 7, 7). The grid size of the discretized tesseroids is $1^{\circ }\times 1^{\circ }$

Table 3 Values of the relative errors in $\log _{10}$ scale using different 3D GLQ orders (n, n, n) (1 $\le n \le 7$) in Fig. 3 by a grid size of $1^{\circ }\times 1^{\circ }$ with one truncated decimal place

In Fig. 3, the points for all GC components (i.e., Band_$\delta V_{zzz}$, Band_$\delta V_{xxz}$, and Band_$\delta V_{yyz}$; Shell_$\delta V_{zzz}$, Shell_$\delta V_{xxz}$, and Shell_$\delta V_{yyz}$) almost overlap together at different 3D GLQ orders for the spherical zonal band and spherical shell, i.e., their relative errors in $\log _{10}$ scale are equal to each other in Table 3. The same rule can be found for all GGT components (i.e., Band_$\delta V_{zz}$, Band_$\delta V_{xx}$, and Band_$\delta V_{yy}$; Shell_$\delta V_{zz}$, Shell_$\delta V_{xx}$, and Shell_$\delta V_{yy}$). In general, regarding the gravitational effects of the single tesseroid and spherical zonal band, as the 3D GLQ orders increase, their relative errors decrease and remain at a certain level of about [$-11$, $-9$]. The relative errors of the gravitational effects of the spherical shell decline with the increased 3D GLQ orders. There is one turning point for the situation of the $\delta V$ with the 3D GLQ orders (3, 3, 3) not only for the single tesseroid in Fig. 3a but also for the spherical zonal band in Fig. 3b. The turning point means that the relative errors of the $\delta V$ at the 3D GLQ orders (3,3,3) are smaller than those at the 3D GLQ orders from (4,4,4) to (7,7,7).

Regarding the relative errors of the single tesseroid and spherical zonal band in Table 3, the values of the $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, and $\delta V_{zzz}$ are correspondingly equal to each other at different 3D GLQ orders. These numerical results reveal that the superposition error (or elimination) effect does not exist for these gravitational components at different 3D GLQ orders. Meanwhile, the relative errors in $\log _{10}$ scale of the gravitational components $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{xxz}$, and $\delta V_{yyz}$ for a spherical zonal band are smaller than those for the single tesseroid at different 3D GLQ orders. This means that the SEEE exists for these gravitational components (i.e., $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{xxz}$, and $\delta V_{yyz}$) when using the strategy of a spherical zonal band discretized into tesseroids. However, at the 3D GLQ orders (3, 3, 3), there exists the abnormal situation that the relative errors of the $\delta V_{xx}$ and $\delta V_{yy}$ for a spherical zonal band are larger than those for the single tesseroid. This may be due to the chosen place of the single tesseroid, which will be investigated using the 3D GLQ orders (3, 3, 3) in the following experiments.

Analogously, for the comparison of the single tesseroid and spherical shell, the relative errors of the spherical shell are larger than those of the single tesseroid with the 3D GLQ orders $1\le n\le 4$ for the $\delta V$ and $\delta V_{r}$, $1\le n\le 5$ for the $\delta V_{xx}$ and $\delta V_{yy}$, $1\le n\le 6$ for the $\delta V_{zz}$, $\delta V_{xxz}$, and $\delta V_{yyz}$, and $1\le n\le 7$ for the $\delta V_{zzz}$. When the 3D GLQ orders are $5\le n\le 7$ for the $\delta V$ and $\delta V_{r}$, $6\le n\le 7$ for the $\delta V_{xx}$ and $\delta V_{yy}$, and $n=7$ for the $\delta V_{zz}$, $\delta V_{xxz}$, and $\delta V_{yyz}$, the relative errors of the spherical shell are smaller than those of the single tesseroid. These results show that the 3D GLQ orders affect the superposition error (or elimination) effect between the single tesseroid and spherical shell. Regarding the spherical shell in relation to the single tesseroid, the superposition error effect exists for lower 3D GLQ orders, while the SEEE is observable for higher 3D GLQ orders.

3.3 Influence of Grid Sizes on Gravitational Effects of the Tesseroid, Spherical Zonal Band, and Spherical Shell

In practical applications, the chosen grid size of the tesseroid has an impact on the accuracy of its calculated gravitational effects. In other words, from the numerical aspect, the grid size of the tesseroids to discretize the spherical zonal band and spherical shell affects the relative errors of the gravitational effects of the single tesseroid, spherical zonal band, and spherical shell. Based on Sect. 3.2, different grid sizes are adopted to investigate the influence of the grid sizes on the gravitational effects of the single tesseroid, spherical zonal band, and spherical shell in this section.

Fig. 4

Visualization of the relative errors of the gravitational effects in $\log _{10}$ scale for (a) the single tesseroid, (b) a spherical zonal band, and (c) a spherical shell with the influence of the grid sizes as $5^{\circ } \times 5^{\circ }$, $2^{\circ } \times 2^{\circ }$, $1^{\circ } \times 1^{\circ }$, $30^{\prime } \times 30^{\prime }$, and $15^{\prime } \times 15^{\prime }$. The applied 3D GLQ orders are (3, 3, 3). Other parameters are the same as in Fig. 3

Due to the fact that the numerical experiment in this section is an extension of that in Sect. 3.2, the numerical settings are the same as those in Sect. 3.2. In order to control the effect of the 3D GLQ orders, the 3D GLQ orders are set as (3, 3, 3). The grid size of the discretized tesseroids are extended from $1^{\circ }\times 1^{\circ }$ to $5^{\circ }\times 5^{\circ }$, $2^{\circ } \times 2^{\circ }$, $30^{\prime } \times 30^{\prime }$, and $15^{\prime } \times 15^{\prime }$. The longitude boundaries of the corresponding single tesseroid are different as [$0^{\circ }$, $5^{\circ }$] for the $5^{\circ }\times 5^{\circ }$, [$0^{\circ }$, $2^{\circ }$] for the $2^{\circ }\times 2^{\circ }$, [$0^{\prime }$, $30^{\prime }$] for the $30^{\prime } \times 30^{\prime }$, and [$0^{\prime }$, $15^{\prime }$] for the $15^{\prime } \times 15^{\prime }$.

Table 4 Values of the points using different gird sizes in Fig. 4 with the 3D GLQ orders (3, 3, 3)

The relative errors of the gravitational effects in $\log _{10}$ scale with different grid sizes for the single tesseroid, spherical zonal band, and spherical shell are shown in Fig. 4, in which their values are listed in Table 4.

In Fig. 4 and Table 4, the relative errors overlap together for the two pairs of $\delta V_{xx}$, $\delta V_{yy}$; $\delta V_{xxz}$, $\delta V_{yyz}$ for the spherical zonal band, and for the two pairs of $\delta V_{zz}$, $\delta V_{xx}$, $\delta V_{yy}$; $\delta V_{zzz}$, $\delta V_{xxz}$, $\delta V_{yyz}$ for the spherical shell. Specifically, in Fig. 4a and Table 4, with the increased grid size of the single tesseroid, the relative errors decrease first and then increase for the GP ($\delta V$), GV ($\delta V_{r}$), and GGT ($\delta V_{zz}$, $\delta V_{xx}$, and $\delta V_{yy}$). Regarding the GC ($\delta V_{zzz}$, $\delta V_{xxz}$, and $\delta V_{yyz}$) of the single tesseroid, their relative errors decrease as the grid sizes increase. In Fig. 4b for the spherical zonal band, the relative errors of the $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, $\delta V_{xx}$, and $\delta V_{yy}$ have the same rules as those for the single tesseroid in Fig. 4a. Regarding the $\delta V_{zzz}$, $\delta V_{xxz}$ and $\delta V_{yyz}$ for the spherical zonal band, their relative errors decrease with the increased grid sizes. In Fig. 4c for the spherical shell, the relative errors of all gravitational components decrease with the increased grid sizes. Regarding some components (i.e., $\delta V$, $\delta V_r$, $\delta V_{zz}$, $\delta V_{xx}$, and $\delta V_{yy}$) of the single tesseroid and the spherical zonal band, the smaller the grid size initially, the smaller the calculation errors, but, once a certain threshold is reached, the smaller the grid size, the larger the calculation errors. One possible explanation is that after a certain threshold is reached, other factors generating the errors are greater than the grid size effects, resulting in the appearance of other faults, e.g., the effects of the GLQ orders.

For the comparison of the single tesseroid and spherical zonal band in Table 4, the relative errors of the $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, and $\delta V_{zzz}$ are correspondingly equal to each other at different grid sizes. These numerical results show that the superposition error (or elimination) effect does not exist for these components at different grid sizes. Regarding the $\delta V_{xx}$ and $\delta V_{yy}$, their relative errors in $\log _{10}$ scale for the spherical zonal band are larger than those for the single tesseroid by the grid sizes of $5^{\circ }\times 5^{\circ }$, $2^{\circ }\times 2^{\circ }$, $1^{\circ }\times 1^{\circ }$ and $30^{\prime }\times 30^{\prime }$. This indicates the existence of the superposition error effect. Regarding the grid size of $15^{\prime }\times 15^{\prime }$ for the $\delta V_{xx}$ and $\delta V_{yy}$, their relative errors in $\log _{10}$ scale for the spherical zonal band (i.e., $-10.1$ and $-10.10$) are smaller than those for the single tesseroid (i.e., $-9.8$ and $-10.06$), which indicates the existence of the SEEE. Similarly, by comparing the relative errors of the $\delta V_{xxz}$ and $\delta V_{yyz}$ between the single tesseroid and spherical zonal band, the SEEE happens for the $\delta V_{xxz}$ and $\delta V_{yyz}$ with the grid sizes $5^{\circ }\times 5^{\circ }$, $2^{\circ }\times 2^{\circ }$, $1^{\circ }\times 1^{\circ }$, and $30^{\prime }\times 30^{\prime }$. Regarding the grid size $15^{\prime }\times 15^{\prime }$, the superposition error effect exists for the $\delta V_{xxz}$, while the SEEE occurs for the $\delta V_{yyz}$.

Regarding the single tesseroid and spherical shell in Fig. 4a, c, and Table 4, the relative errors of the GGT ($\delta V_{zz}$, $\delta V_{xx}$, and $\delta V_{yy}$) and GC ($\delta V_{zzz}$, $\delta V_{xxz}$, and $\delta V_{yyz}$) for the spherical shell are larger than those for the single tesseroid at different grid sizes (i.e., $5^{\circ }\times 5^{\circ }$, $2^{\circ }\times 2^{\circ }$, $1^{\circ }\times 1^{\circ }$, $30^{\prime }\times 30^{\prime }$, and $15^{\prime }\times 15^{\prime }$). Meanwhile, this rule can also be found for the relative errors of the GP ($\delta V$) and GV ($\delta V_{r}$) for the spherical shell with the grid sizes $5^{\circ }\times 5^{\circ }$, $2^{\circ }\times 2^{\circ }$, $1^{\circ }\times 1^{\circ }$, and $30^{\prime }\times 30^{\prime }$. These numerical results indicate the existence of the superposition error effect for the numerical strategy of a spherical shell discretized into tesseroids. However, for the grid size $15^{\prime }\times 15^{\prime }$ of the $\delta V$ and $\delta V_{r}$, the numerical results of the relative errors between the single tesseroid and spherical shell reveal that the SEEE happens in current situation.

3.4 Comparison of Gravitational Effects of Every Individual Tesseroid Forming the Whole Spherical Zonal Band and Spherical Shell

In previous numerical experiments in Sects. 3.2 and 3.3, the location of the single tesseroid was based on a specific tesseroid, i.e., the first tesseroid in the longitude direction at different grid sizes. To comprehensively investigate the superposition error (or elimination) effect of the spherical zonal band and spherical shell discretized into tesseroids, the specific single tesseroid is extended to every individual tesseroid forming the whole spherical zonal band and spherical shell. In other words, the relative errors of the gravitational effects (i.e., GP, GV, GGT, and GC) of every individual tesseroid forming the whole spherical zonal band and spherical shell are studied in this section.

The numerical settings in this section are the same as those in Sect. 3.3. The 3D GLQ orders are set as (3, 3, 3), and the grid size of the discretized tesseroids is $1^{\circ }\times 1^{\circ }$. This simplifies the numerical experiment in this section, in which the effects of the 3D GLQ orders and grid size are explored numerically in Sects. 3.2 and 3.3, respectively. The relative errors of the gravitational effects in $\log _{10}$ scale for each individual tesseroid forming the whole spherical zonal band are illustrated in Fig. 5a. Note that these relative errors are calculated based on the reference values and calculated values of each individual tesseroid. After subtracting the relative errors of the gravitational effects in $\log _{10}$ scale for the spherical zonal band discretized using tesseroid (i.e., these values are listed in Table 4 with the grid size $1^{\circ }\times 1^{\circ }$) based on the corresponding numerical values in Fig. 5a, their differences of the relative errors in $\log _{10}$ scale of the gravitational effects are shown in Fig. 5b. Meanwhile, the statistical information of the values in Fig. 5 is listed in Table 5.

When calculating the relative errors of the gravitational effects for every individual tesseroid forming the whole spherical shell, the $\ln (0)$ occurs for the reference values of the gravitational effects (e.g., V, $V_{r}$, $V_{zz}$, $V_{xx}$, and $V_{yy}$) with the colatitude of the integration point $\theta _1=0^{\circ }$. Thus, the relative errors of the gravitational effects with the first number of the colatitude for the tesseroids forming the whole spherical shell are dropped. The number of the colatitude for every individual tesseroid is [2, 180] with the grid size $1^{\circ }\times 1^{\circ }$. Then, the relative errors of the gravitational effects in $\log _{10}$ scale for each individual tesseroid totally forming the spherical shell along the colatitude direction with the first longitude profile are shown in Fig. 6a, where the first longitude profile is chosen to reveal the variation in the relative errors. In this numerical experiment, the first longitude is from $0^{\circ }$ to $1^{\circ }$ due to the grid size of $1^{\circ }\times 1^{\circ }$. Similarly, after subtracting the relative errors of the gravitational effects in $\log _{10}$ scale for a spherical shell discretized into tesseroids (i.e., these values are listed in Table 4 with the grid size $1^{\circ }\times 1^{\circ }$) based on the numerical results in Fig. 6a, their differences of the gravitational effects are shown in Fig. 6b. The statistical information of the values in Fig. 6 is listed in Table 6.

Fig. 5

Illustration of (a) the relative errors of the gravitational effects in $\log _{10}$ scale for each individual tesseroid totally forming the whole spherical zonal band; (b) the difference of the relative errors of the gravitational effects in $\log _{10}$ scale between each individual tesseroid and a spherical zonal band discretized into tesseroids. The x-axis means the counter of the individual tesseroid along the longitude direction. The grid size of the discretized tesseroids is $1^{\circ }\times 1^{\circ }$ and the 3D GLQ orders are (3, 3, 3)

Table 5 Statistical information of the values in Fig. 5, where Min, Max, Mean, STD, and RMS are the values of the minimum, maximum, average, standard derivation, and root mean square with one truncated decimal place

Fig. 6

Visualization of (a) the relative errors of the gravitational effects in $\log _{10}$ scale for each individual tesseroid totally forming the spherical shell along the colatitude direction with the first longitude profile; (b) the difference of the relative errors of the gravitational effects in $\log _{10}$ scale between each individual tesseroid and a spherical shell discretized into tesseroids. The x-axis means the colatitude of the discretized tesseroid. Other parameters are the same as in Fig. 5

Table 6 Statistical information of the values in Fig. 6, where other information is the same in Table 5

Moreover, the relative errors in $\log _{10}$ scale of the gravitational effects for every individual tesseroid forming the whole spherical shell are also calculated and their statistical values are listed in Table 7. After subtracting the relative errors of the gravitational effects in $\log _{10}$ scale for a spherical shell, the differences of the relative errors in $\log _{10}$ scale of the gravitational effects are obtained, and their statistical values are also listed in Table 7.

In Fig. 5a, the relative errors of the $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, and $\delta V_{zzz}$ appear as distinct straight lines, which indicates that their values are not affected by changes in longitude of each individual tesseroid. Regarding the $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{xxz}$, and $\delta V_{yyz}$, their relative errors exhibit periodic changes as longitude changes. The period of change is about $180^{\circ }$. In Fig. 5b, the differences of the $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, and $\delta V_{zzz}$ are about zero, which reveals that the superposition error (or elimination) effect does not exist for these components by using the strategy of a spherical zonal band discretized into tesseroids. Regarding the $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{xxz}$, and $\delta V_{yyz}$, their differences are related to the position of the individual tesseroid along the longitude direction. From Table 5, the mean values of the differences are about 0.3 for the $\delta V_{xx}$ and $\delta V_{yy}$ and $-0.1$ for the $\delta V_{xxz}$ and $\delta V_{yyz}$. These numerical values reveal that on the overall average, the SEEE occurs for the $\delta V_{xx}$ and $\delta V_{yy}$, and the superposition error effect exists for the $\delta V_{xxz}$ and $\delta V_{yyz}$.

In Fig. 6a, as the colatitude increases, all curves first drop sharply, then oscillates erratically, and finally rise. In Fig. 6b, except for a small number of the values below zero at the beginning, all subsequent values are greater than zero. These results reveal that the SEEE occurs for the spherical shell discretized into tesseroids in the most cases. This effect can be confirmed not only by the mean values of the differences in Table 6 as 1.8 for the $\delta V$, 3.7 for the $\delta V_{r}$, 5.3 for the $\delta V_{zz}$, 4.8 for the $\delta V_{xx}$, 5.2 for the $\delta V_{yy}$, 6.9 for the $\delta V_{zzz}$, $\delta V_{xxz}$, and 7.0 for the $\delta V_{yyz}$, but also by the mean values of the differences in Table 7 as 1.8 for the $\delta V$, 3.7 for the $\delta V_{r}$, 5.3 for the $\delta V_{zz}$, 5.1 for the $\delta V_{xx}$, $\delta V_{yy}$, and 6.9 for the $\delta V_{zzz}$, $\delta V_{xxz}$, $\delta V_{yyz}$.

Table 7 Statistical information of the values for the relative errors in $\log _{10}$ scale of the gravitational effects for every individual tesseroid forming the whole spherical shell and the differences of the relative errors in $\log _{10}$ scale of the gravitational effects between every individual tesseroid and the spherical shell

4 Conclusions and Outlook

Previous studies investigated the gravitational effects of a tesseroid by different numerical approaches. Meanwhile, the integrals in the expressions for the gravitational effects of a tesseroid were often considered not to be integrated analytically. In this contribution, the analytical expressions for the gravitational effects (i.e., GP, GV, GGT, and GC) of a tesseroid are derived when the computation point is located on the polar axis. Based on the relation between the tesseroid and the spherical zonal band, the simpler analytical expressions for the gravitational effects of a spherical zonal band are derived in comparison with previous studies. In addition, the analytical expressions for the gravitational effects of a spherical shell are presented based on the relation between the tesseroid and the spherical shell.

These new analytical formulas of the GGT and GC of the tesseroid and spherical zonal band are confirmed to be correct by using Laplace’s equation. Meanwhile, the consistency of the analytical expressions for the gravitational effects of a spherical zonal band between Deng (2022) and this paper is confirmed in Appendix F.

The influence of the 3D GLQ orders from (1, 1, 1) to (7, 7, 7) on the gravitational effects of the single tesseroid, spherical zonal band, and spherical shell is investigated with the grid size $1^{\circ }\times 1^{\circ }$. As the 3D GLQ orders increase, the relative errors of the gravitational effects of the single tesseroid and spherical zonal band decrease and remain at a certain level. For the spherical shell, the relative errors decline with the increased 3D GLQ orders. Comparing the single tesseroid and spherical zonal band, the superposition error (or elimination) effect does not exist for these gravitational components (i.e., $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, and $\delta V_{zzz}$) at different 3D GLQ orders. Regarding other gravitational components (i.e., $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{xxz}$, and $\delta V_{yyz}$), the SEEE mainly occurs. For the single tesseroid and spherical shell, the 3D GLQ orders have an impact on the superposition error (or elimination) effect. Specifically, the superposition error effect exists for lower 3D GLQ orders, and the SEEE exists for higher 3D GLQ orders.

The influence of the grid sizes on the gravitational effects of the single tesseroid, spherical zonal band, and spherical shell is investigated with the 3D GLQ order (3, 3, 3). As the grid sizes decrease from $5^{\circ }\times 5^{\circ }$ to $15^{\prime }\times 15^{\prime }$, the relative errors decline first and then increase for the $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, $\delta V_{xx}$, and $\delta V_{yy}$ of the single tesseroid and spherical zonal band. The relative errors decline with the finer grid sizes not only for the $\delta V_{zzz}$, $\delta V_{xxz}$, and $\delta V_{yyz}$ of the single tesseroid and spherical zonal band but also for all gravitational effects (i.e., $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{zzz}$, $\delta V_{xxz}$, and $\delta V_{yyz}$) of the spherical shell. For the comparison between the single tesseroid and spherical zonal band, the superposition error (or elimination) effect does not occur for these gravitational components (i.e., $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, and $\delta V_{zzz}$) with different grid sizes. Regarding the $\delta V_{xx}$ and $\delta V_{yy}$, the superposition error effect exists with the grid sizes $5^{\circ }\times 5^{\circ }$, $2^{\circ }\times 2^{\circ }$, $1^{\circ }\times 1^{\circ }$, and $30^{\prime }\times 30^{\prime }$ and the SEEE occurs with the grid size $15^{\prime }\times 15^{\prime }$. On the contrary, regarding the $\delta V_{xxz}$ and $\delta V_{yyz}$, the SEEE happens with the grid sizes $5^{\circ }\times 5^{\circ }$, $2^{\circ }\times 2^{\circ }$, $1^{\circ }\times 1^{\circ }$, and $30^{\prime }\times 30^{\prime }$. The superposition error effect occurs for the $\delta V_{xxz}$ and $\delta V_{yyz}$ with the grid size $15^{\prime }\times 15^{\prime }$. Regarding the comparison between the single tesseroid and spherical shell, numerical results show that the superposition error effect happens for the gravitational effects of the spherical shell discretized into tesseroids with different grid sizes, except for the $\delta V$ and $\delta V_{r}$ with the grid size $15^{\prime }\times 15^{\prime }$.

The superposition error (or elimination) effect is investigated for the gravitational effects of every individual tesseroid forming the whole spherical zonal band and spherical shell with the grid size $1^{\circ }\times 1^{\circ }$ and 3D GLQ orders (3, 3, 3). Numerical results show that the superposition error (or elimination) effect does not exist for the $\delta V$, $\delta V_{r}$, $\delta V_{zz}$, and $\delta V_{zzz}$ by using the strategy of a spherical zonal band discretized into tesseroids. Regarding the $\delta V_{xx}$, $\delta V_{yy}$, $\delta V_{xxz}$, and $\delta V_{yyz}$ of the spherical zonal band, the SEEE occurs for the $\delta V_{xx}$ and $\delta V_{yy}$, and the superposition error effect exists for the $\delta V_{xxz}$ and $\delta V_{yyz}$ on the overall average. Regarding a spherical shell discretized into tesseroids, the SEEE occurs for this strategy in most cases.

In short, these numerical experiments confirm the existence of the SEEE hypothesis. When using the tesseroids in practical applications of gravity field modeling, the local error assessment by using the analytical formulas of the GP, GV, GGT, and GC of a tesseroid of this paper will be performed necessarily in the future study. Due to the existence of the SEEE and superposition error effect, the benchmark of a spherical zonal band and a spherical shell discretized into small mass bodies should be employed with caution in gravity field modeling in geodesy and geophysics. Their numerical results only pertain to the global situation as a whole spherical zonal band or a whole spherical shell, not the local one.

The new strategy of a reference tesseroid with respect to its calculated tesseroid can be proposed in comparison with the commonly used strategies of a spherical zonal band and a spherical shell discretized into tesseroids. The mathematical derivations using the spherical coordinates $\lambda$, $\theta$, and r in the paper can also be performed by using the spherical polar coordinates $\alpha$ and $\psi$ (Novák et al. 2017, 2019). Meanwhile, the coordinate system transformation of the higher-order gravitational gradients will be investigated in the near future. In future studies, these new derived analytical formulas of the gravitational effects of a tesseroid can serve as reference values for the evaluation of the calculated gravitational effects of the tesseroid by using not only the above-mentioned numerical methods but also other numerical approaches, e.g., spherical harmonics (Ramillien 2017; Baykiev et al. 2020; Šprlák et al. 2020). Future research will investigate the comparison of these numerical approaches to calculate the volume or surface integrals of the tesseroid. Compared with the spherical zonal band and spherical shell, the variation in the relative errors of the gravitational effects of the tesseroid can be revealed from a more subtle perspective. The SEEE can be extended to an arbitrary mass body that can be discretized into smaller mass bodies not only in the spatial domain but also in the spectral domain. On the basis of this paper, the higher-order gravitational potential gradient (e.g., the fourth-order gravitational potential gradient (Deng and Ran 2021) and first-order derivatives of the invariants of the GGT (Deng et al. 2021)) of a tesseroid can also be derived analytically when the computation point is located on the polar axis. Finally, based on the results of this study in the gravity field, it can be extended to the magnetic field. In other words, the analytical expressions for the magnetic effects of a tesseroid can be derived in the magnetic field.

Appendices

Appendix A

Derivation of the Analytical Expression for the GP of a Tesseroid

When the computation point is located on the polar axis and $\theta = 0$, Eq. (3) becomes

$$\begin{aligned} \cos \psi = \cos \theta ^{\prime } \end{aligned}$$

(36)

and substituting Eq. (36) into Eq. (2) yields:

$$\begin{aligned} l^{2} = r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime } \end{aligned}$$

(37)

Differentiating Eq. (37) with respect to the $\theta ^{\prime }$ yields:

$$\begin{aligned} 2 l \frac{\textrm{d} l}{\textrm{d} \theta ^{\prime }} = 2 r r^{\prime } \sin \theta ^{\prime } \end{aligned}$$

(38)

After the simple mathematical transformation, Eq. (38) becomes:

$$\begin{aligned} \sin \theta ^{\prime } \textrm{d} \theta ^{\prime } = \frac{l}{r r^{\prime }} \textrm{d} l \end{aligned}$$

(39)

Substituting Eq. (39) into Eq. (1) yields:

$$\begin{aligned} \begin{aligned} V&= G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{l_{1}}^{l_{2}} \frac{{r^{\prime }}^{2}}{l} \frac{l}{r r^{\prime }} \textrm{d} l \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{l_{1}}^{l_{2}} \frac{r^{\prime }}{r} \textrm{d} l \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= \frac{G \rho }{r} \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} r^{\prime }\ \big [l\big ]\big \vert _{l_{1}}^{l_{2}} \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= \frac{G \rho (\lambda _2 - \lambda _1)}{r} \int _{r_{1}}^{r_{2}} r^{\prime } (l_{2} - l_{1}) \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(40)

where $l_2 = \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2}$ and $l_1=\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1}$.

In Eq. (40), $\begin{aligned} \int _{r_{1}}^{r_{2}} r^{\prime } l_{2} \textrm{d} r^{\prime } \end{aligned}$ is obtained as:

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} r^{\prime } \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _{2}}\ \textrm{d} r^{\prime } \\&\quad = \frac{1}{12} \Big [ \big (r^{2} + 4 {r^{\prime }}^{2} -2 r r^{\prime } \cos \theta _{2} - 3 r^{2} \cos 2 \theta _{2} \big ) \sqrt{r^2 + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _{2} } \\&\quad \quad + 6 r^3 \sin ^{2} \theta _{2} \cos \theta _{2} \ln \Big ( r^{\prime } - r \cos \theta _{2} + \sqrt{r^2 + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _{2} }\Big ) \Big ]\Big \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(41)

and $\begin{aligned} \int _{r_{1}}^{r_{2}} - r^{\prime } l_{1} \textrm{d} r^{\prime } \end{aligned}$ is obtained as:

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} - r^{\prime } \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _{1}}\ \textrm{d} r^{\prime } \\&\quad = - \frac{1}{12} \Big [ \big (r^{2} + 4 {r^{\prime }}^{2} -2 r r^{\prime } \cos \theta _{1} - 3 r^{2} \cos 2 \theta _{1} \big ) \sqrt{r^2 + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _{1} } \\&\quad \quad + 6 r^3 \sin ^{2} \theta _{1} \cos \theta _{1} \ln \Big (r^{\prime } - r \cos \theta _{1} + \sqrt{r^2 + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _{1} } \Big ) \Big ]\Big \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(42)

After substituting Eqs. (41) and (42) into Eq. (40), the analytical formula of the GP of a tesseroid when the computation point is located on the polar axis is obtained in Eq. (4).

Table 8 Detailed expressions for the $A_{22}$, $A_{12}$, $A_{21}$, $A_{11}$, $B_{2}$, $B_{1}$, $C_{22}$, $C_{12}$, $C_{21}$, $C_{11}$, $l_{22}$, $l_{12}$, $l_{21}$, and $l_{11}$ for the GP (V) in Eq. (4)

Appendix B

Derivation of the Analytical Expression for the GV of a Tesseroid

When the colatitude of the computation point is $\theta = 0$, substituting Eq. (36) into Eq. (6) yields:

$$\begin{aligned} \Delta _z = r^{\prime } \cos \theta ^{\prime } -r \end{aligned}$$

(43)

and Eq. (37) can be transformed into:

$$\begin{aligned} r^{\prime } \cos \theta ^{\prime } -r = - \frac{l^2+r^2-{r^{\prime }}^{2}}{2 r} \end{aligned}$$

(44)

Substituting Eqs. (39), (43) and (44) into Eq. (5) yields:

$$\begin{aligned} \begin{aligned} {V_{r} }&= G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{l_{1}}^{l_{2}} \frac{{r^{\prime }}^{2}}{l^{3}} \Big ( - \frac{l^2+r^2-{r^{\prime }}^{2}}{2 r} \Big ) \frac{l}{r r^{\prime }} \textrm{d} l \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= - \frac{G \rho }{2 r^2} \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{l_{1}}^{l_{2}} \frac{r^{\prime }(l^2+r^2-{r^{\prime }}^{2})}{l^2} \textrm{d} l \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= - \frac{G \rho }{2 r^2} \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \Big [r^{\prime } \Big (l - \frac{r^2-{r^{\prime }}^{2}}{l} \Big ) \Big ]\Big \vert _{l_{1}}^{l_{2}} \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= - \frac{G \rho (\lambda _2 - \lambda _1)}{2 r^2} \int _{r_{1}}^{r_{2}} \Big [r^{\prime } \Big (l_{2} - \frac{r^2-{r^{\prime }}^{2}}{l_{2}} \Big ) - r^{\prime } \Big (l_{1} - \frac{r^2-{r^{\prime }}^{2}}{l_{1}} \Big ) \Big ] \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(45)

In Eq. (45), $\begin{aligned} \int _{r_{1}}^{r_{2}} r^{\prime } \Big (l_{2} - \frac{r^2-{r^{\prime }}^{2}}{l_{2}} \Big ) \textrm{d} r^{\prime } \end{aligned}$ becomes:

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} r^{\prime } \Big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2} - \frac{r^2-{r^{\prime }}^{2}}{\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2}} \Big ) \textrm{d} r^{\prime } \\&\quad = \Big [ \frac{2}{3} \big (-2 r^2 + {r^{\prime }}^{2} + r r^{\prime } \cos \theta _{2} + 3 r^{2} \cos ^2 \theta _{2} \big ) \sqrt{r^2+{r^{\prime }}^{2}-2 r r^{\prime } \cos \theta _{2}} \\&\quad - 2 r^3 \sin ^2 \theta _{2} \cos \theta _{2} \ln \Big (r^{\prime }-r \cos \theta _{2} + \sqrt{r^2+{r^{\prime }}^{2}-2 r r^{\prime } \cos \theta _{2}} \Big ) \Big ] \Big \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(46)

and $\begin{aligned} \int _{r_{1}}^{r_{2}} - r^{\prime } \Big (l_{1} - \frac{r^2-{r^{\prime }}^{2}}{l_{1}} \Big ) \textrm{d} r^{\prime } \end{aligned}$ becomes:

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} - r^{\prime } \Big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1} - \frac{r^2-{r^{\prime }}^{2}}{\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1}} \Big ) \textrm{d} r^{\prime } \\&\quad = \Big [ - \frac{2}{3} \big (-2 r^2 + {r^{\prime }}^{2} + r r^{\prime } \cos \theta _{1} + 3 r^{2} \cos ^2 \theta _{1} \big ) \sqrt{r^2+{r^{\prime }}^{2}-2 r r^{\prime } \cos \theta _{1}} \\&\quad + 2 r^3 \sin ^2 \theta _{1} \cos \theta _{1} \ln \Big ( r^{\prime }-r \cos \theta _{1} + \sqrt{r^2+{r^{\prime }}^{2}-2 r r^{\prime } \cos \theta _{1}} \Big ) \Big ] \Big \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(47)

After substituting Eqs. (46) and (47) into Eq. (45), the analytical formula of the radial GV of a tesseroid when the computation point is located on the polar axis is obtained in Eq. (7).

Table 9 Detailed expressions for the $D_{22}$, $D_{12}$, $D_{21}$, and $D_{11}$ for the radial GV ($V_r$) in Eq. (7)

Regarding the analytical expressions for the $V_{x}$ and $V_{y}$ of a tesseroid, their derivations are presented in the Mathematica code GV_VxVy.nb at the link https://github.com/xiaoledeng/analytical-tesseroid-spherical-zonal-band.

Appendix C

Derivation of the Analytical Expressions for the GGT of a Tesseroid

Table 10 Detailed expressions for the $E_{22}$, $E_{12}$, $E_{21}$, and $E_{11}$ for the radial-radial GGT ($V_{rr}$) in Eq. (9)

Table 11 Detailed expressions for the $F_{2}$, $F_{1}$, $H_{2}$, $H_{1}$, $I_{22}$, $I_{12}$, $I_{21}$, $I_{11}$, $J_2$, $J_1$, $K_{22}$, $K_{12}$, $K_{21}$, and $K_{11}$ for the $V_{xx}$ in Eq. (14)

Table 12 Detailed expressions for the $L_{2}$, $L_{1}$, $M_{22}$, $M_{12}$, $M_{21}$, $M_{11}$, $N_{22}$, $N_{12}$, $N_{21}$, and $N_{11}$ for the $V_{yy}$ in Eq. (15)

When the colatitude of the computation point is $\theta =0$, substituting Eqs. (39), (43), and (44) into Eq. (5) yields:

$$\begin{aligned} \begin{aligned}&{V_{rr} } = G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{l_{1}}^{l_{2}} {r^{\prime }}^{2} \Big [ \frac{3 }{l^{5}} (- \frac{l^2+r^2-{r^{\prime }}^{2}}{2 r})^2 - \frac{1}{l^{3}} \Big ] \frac{l}{r r^{\prime }} \textrm{d} l \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= \frac{G \rho }{4 r^3} \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{l_{1}}^{l_{2}} \frac{r^{\prime }\big [ 3 l^4 + 2 l^2 (r^2 - 3 {r^{\prime }}^{2}) + 3 (r^2 - {r^{\prime }}^{2} )^2 \big ]}{l^4} \textrm{d} l \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= \frac{G \rho }{4 r^3} \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} r^{\prime } \Big [ 3 l - \frac{2(r^2 - 3 {r^{\prime }}^{2})}{l} - \frac{(r^2 - {r^{\prime }}^{2} )^2}{l^3} \Big ] \Big \vert _{l_{1}}^{l_{2}} \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&= \frac{G \rho (\lambda _2 - \lambda _1)}{4 r^3} \int _{r_{1}}^{r_{2}} \Big \{ r^{\prime } \Big [ 3 l_{2} - \frac{2(r^2 - 3 {r^{\prime }}^{2})}{l_{2}} - \frac{(r^2 - {r^{\prime }}^{2} )^2}{{l_{2}}^3} \Big ]\\&- r^{\prime } \Big [ 3 l_{1} - \frac{2(r^2 - 3 {r^{\prime }}^{2})}{l_{1}} - \frac{(r^2 - {r^{\prime }}^{2} )^2}{{l_{1}}^3} \Big ] \Big \} \textrm{d} r^{\prime } \\ \end{aligned} \end{aligned}$$

(48)

In Eq. (48), $\begin{aligned} \int _{r_{1}}^{r_{2}} r^{\prime } \Big [ 3 l_{2} - \frac{2(r^2 - 3 {r^{\prime }}^{2})}{l_{2}} - \frac{(r^2 - {r^{\prime }}^{2} )^2}{{l_{2}}^3} \Big ] \textrm{d} r^{\prime } \end{aligned}$ is calculated by

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} r^{\prime } \Big [ 3 \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2} - \frac{2(r^2 - 3 {r^{\prime }}^{2})}{\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2}} - \frac{(r^2 - {r^{\prime }}^{2} )^2}{ \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2} \big )^3} \Big ] \textrm{d} r^{\prime } \\&\quad = \frac{2}{3} \Big [ \frac{r^4 + r^2 {r^{\prime }}^{2} + 4 {r^{\prime }}^{4} - r r^{\prime } (r^2 + 4 {r^{\prime }}^{2}) \cos \theta _{2} - r^2 (3 r^2 + {r^{\prime }}^{2}) \cos 2 \theta _{2} + 3 r^3 r^{\prime } \cos 3 \theta _{2}}{\sqrt{r^2 + {r^{\prime }}^{2} -2 r r^{\prime } \cos \theta _{2} }} \\&\quad + 6 r^3 \sin ^2 \theta _{2} \cos \theta _{2} \ln \Big ( r^{\prime }-r \cos \theta _{2} + \sqrt{r^2 + {r^{\prime }}^{2} -2 r r^{\prime } \cos \theta _{2} } \Big ) \Big ] \Big \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(49)

and $\begin{aligned} \int _{r_{1}}^{r_{2}} - r^{\prime } \Big [ 3 l_{1} - \frac{2(r^2 - 3 {r^{\prime }}^{2})}{l_{1}} - \frac{(r^2 - {r^{\prime }}^{2} )^2}{{l_{1}}^3} \Big ] \textrm{d} r^{\prime } \end{aligned}$ is calculated by

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} - r^{\prime } \Big [ 3 \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1} - \frac{2(r^2 - 3 {r^{\prime }}^{2})}{\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1}} - \frac{(r^2 - {r^{\prime }}^{2} )^2}{ \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1} \big )^3} \Big ] \textrm{d} r^{\prime } \\&\quad = - \frac{2}{3} \Big [ \frac{r^4 + r^2 {r^{\prime }}^{2} + 4 {r^{\prime }}^{4} - r r^{\prime } (r^2 + 4 {r^{\prime }}^{2}) \cos \theta _{1} - r^2 (3 r^2 + {r^{\prime }}^{2}) \cos 2 \theta _{1} + 3 r^3 r^{\prime } \cos 3 \theta _{1}}{\sqrt{r^2 + {r^{\prime }}^{2} -2 r r^{\prime } \cos \theta _{1} }} \\&\quad + 6 r^3 \sin ^2 \theta _{1} \cos \theta _{1} \ln \Big ( r^{\prime }-r \cos \theta _{1} + \sqrt{r^2 + {r^{\prime }}^{2} -2 r r^{\prime } \cos \theta _{1} } \Big ) \Big ] \Big \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(50)

After substituting Eqs. (49) and (50) into Eq. (48), the analytical formula of the radial–radial GGT of a tesseroid when the computation point is located on the polar axis is presented in Eq. (9).

Regarding the analytical expression for the $V_{xx}$ with the colatitude of the computation point $\theta = 0$, Eq. (11) becomes

$$\begin{aligned} \Delta _x = - r^{\prime } \sin \theta ^{\prime } \cos (\lambda ^{\prime } - \lambda ) \end{aligned}$$

(51)

Substituting Eqs. (37) and (51) into Eq. (10) yields:

$$\begin{aligned} \begin{aligned} V_{xx}&= G \rho \int _{r_{1}}^{r_{2}} \int _{\theta _{1}}^{\theta _{2}} \int _{\lambda _{1}}^{\lambda _{2}} {r^{\prime }}^{2} \sin \theta ^{\prime } \bigg [ \frac{3 \big [ - r^{\prime } \sin \theta ^{\prime } \cos (\lambda ^{\prime } - \lambda )\big ]^2}{\big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{5}} \\&\quad - \frac{1}{\big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{3}} \bigg ] \textrm{d} \lambda ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&= G \rho \int _{r_{1}}^{r_{2}} \int _{\theta _{1}}^{\theta _{2}} \frac{ {r^{\prime }}^{2} \sin \theta ^{\prime } }{4 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{5} } \bigg [ -4 (r^2 + {r^{\prime }}^2) \lambda ^{\prime } + 8 r r^{\prime } \cos \theta ^{\prime } \lambda ^{\prime } \\&\quad - 3 {r^{\prime }}^2 \sin ^2 \theta ^{\prime } \big [ 2 \lambda - 2 \lambda ^{\prime } + \sin 2(\lambda -\lambda ^{\prime }) \big ] \bigg ] \bigg \vert _{\lambda _{1}}^{\lambda _{2}} \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&= G \rho \int _{r_{1}}^{r_{2}} \int _{\theta _{1}}^{\theta _{2}} \frac{ {r^{\prime }}^{2} \sin \theta ^{\prime } }{4 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{5} } \bigg [ 6 {r^{\prime }}^{2} \sin ^2 \theta ^{\prime } \sin (\lambda _2 - \lambda _1 ) \cos (2 \lambda - \lambda _1 - \lambda _2) \\&\quad - (\lambda _2 - \lambda _1 ) (4 r^2 + {r^{\prime }}^{2} - 8 r r^{\prime } \cos \theta ^{\prime } + 3 {r^{\prime }}^{2} \cos 2 \theta ^{\prime } ) \bigg ] \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&= G \rho \int _{r_{1}}^{r_{2}} \bigg \{ \frac{r^{\prime }}{8 r^3 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{3}} \bigg [ r r^{\prime } \Big [ 8 (r^2 + 3 {r^{\prime }}^{2} ) (\lambda _2 - \lambda _1) \cos \theta ^{\prime } \\&\quad - 3 r r^{\prime } \cos 2 \theta ^{\prime } \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2 (\lambda - \lambda _1) - \sin 2 (\lambda - \lambda _2) \big ] \Big ] \\&\quad - 2 \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 4r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 - 12 r r^{\prime } (r^2 + {r^{\prime }}^2) \cos \theta ^{\prime } \big ] \\&\quad -2 {r^{\prime }}^2 (9 r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1) \bigg ] \bigg \} \bigg \vert _{\theta _{1}}^{\theta _{2}} \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(52)

where in Eq. (52),

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} \frac{r^{\prime }}{8 r^3 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2}\big )^{3}} \bigg [ r r^{\prime } \Big [ 8 (r^2 + 3 {r^{\prime }}^{2} ) (\lambda _2 - \lambda _1) \cos \theta _2 \\&\quad - 3 r r^{\prime } \cos 2 \theta _2 \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2 (\lambda - \lambda _1) - \sin 2 (\lambda - \lambda _2) \big ] \Big ] \\&\quad - 2 \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 4r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 - 12 r r^{\prime } (r^2 + {r^{\prime }}^2) \cos \theta _2 \big ] \\&\quad -2 {r^{\prime }}^2 (9 r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1) \bigg ] \textrm{d} r^{\prime } \\&\quad = \frac{1}{48} \bigg [ - 3 \cos \theta _2 \big [ 8 (\lambda _2 - \lambda _1 ) \sin ^2 \theta _2 \\&\quad + 4 \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) (5-\cos 2 \theta _2) \big ] \ln \Big ( r^{\prime } - r \cos \theta _2 + \sqrt{r^2 + {r^{\prime }}^2 - 2 r r^{\prime } \cos \theta _2 } \Big ) \\&\quad + \frac{1}{r^3 \sqrt{r^2 + {r^{\prime }}^2 - 2 r r^{\prime } \cos \theta _2 }} \Big [ -4 (r^4 + r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 ) (\lambda _2 - \lambda _1) \\&\quad + 2 r^2 \big [ (3r^2 + {r^{\prime }}^2 ) \cos 2 \theta _2 - 3 r r^{\prime } \cos 3 \theta _2 \big ] \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2(\lambda - \lambda _1) - \sin 2(\lambda - \lambda _2) \big ] \\&\quad - 4 (13 r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 ) \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1 ) \\&\quad + 4 r r^{\prime } \cos \theta _2 \big [ (r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1 )+ (25r^2 + 4 {r^{\prime }}^2) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ] \Big ] \bigg ] \bigg \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(53)

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} - \frac{r^{\prime }}{8 r^3 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1}\big )^{3}} \bigg [ r r^{\prime } \Big [ 8 (r^2 + 3 {r^{\prime }}^{2} ) (\lambda _2 - \lambda _1) \cos \theta _1 \\&\quad - 3 r r^{\prime } \cos 2 \theta _1 \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2 (\lambda - \lambda _1) - \sin 2 (\lambda - \lambda _2) \big ] \Big ] \\&\quad - 2 \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 4r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 - 12 r r^{\prime } (r^2 + {r^{\prime }}^2) \cos \theta _1 \big ] \\&\quad -2 {r^{\prime }}^2 (9 r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1) \bigg ] \textrm{d} r^{\prime } \\&\quad = - \frac{1}{48} \bigg [ - 3 \cos \theta _1 \big [ 8 (\lambda _2 - \lambda _1 ) \sin ^2 \theta _1 \\&\quad + 4 \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) (5-\cos 2 \theta _1) \big ] \ln \Big ( r^{\prime } - r \cos \theta _1 + \sqrt{r^2 + {r^{\prime }}^2 - 2 r r^{\prime } \cos \theta _1 } \Big ) \\&\quad + \frac{1}{r^3 \sqrt{r^2 + {r^{\prime }}^2 - 2 r r^{\prime } \cos \theta _1 }} \Big [ -4 (r^4 + r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 ) (\lambda _2 - \lambda _1) \\&\quad + 2 r^2 \big [ (3r^2 + {r^{\prime }}^2 ) \cos 2 \theta _1 - 3 r r^{\prime } \cos 3 \theta _1 \big ] \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2(\lambda - \lambda _1) - \sin 2(\lambda - \lambda _2) \big ] \\&\quad - 4 (13 r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 ) \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1 ) \\&\quad + 4 r r^{\prime } \cos \theta _1 \big [ (r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1 )+ (25r^2 + 4 {r^{\prime }}^2) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ] \Big ] \bigg ] \bigg \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(54)

After substituting Eqs. (53) and (54) into Eq. (52), the analytical solution for the $V_{xx}$ of a tesseroid with the computation point located on the polar axis is obtained in Eq. (14).

Similarly, regarding the analytical solution for the $V_{yy}$ with the colatitude of the computation point $\theta = 0$, substituting Eqs. (13) and (37) into Eq. (12) yields:

$$\begin{aligned} \begin{aligned} V_{yy}&= G \rho \int _{r_{1}}^{r_{2}} \int _{\theta _{1}}^{\theta _{2}} \int _{\lambda _{1}}^{\lambda _{2}} {r^{\prime }}^{2} \sin \theta ^{\prime } \bigg [ \frac{3 \big [r^{\prime } \sin \theta ^{\prime } \sin (\lambda ^{\prime }-\lambda ) \big ]^2}{\big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{5}} \\&\quad - \frac{1}{\big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{3}} \bigg ] \textrm{d} \lambda ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&= G \rho \int _{r_{1}}^{r_{2}} \int _{\theta _{1}}^{\theta _{2}} \frac{ {r^{\prime }}^{2} \sin \theta ^{\prime } }{4 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{5} } \bigg [ -4 (r^2 + {r^{\prime }}^2) \lambda ^{\prime } + 8 r r^{\prime } \cos \theta ^{\prime } \lambda ^{\prime } \\&\quad - 3 {r^{\prime }}^2 \sin ^2 \theta ^{\prime } \big [ 2 \lambda - 2 \lambda ^{\prime } - \sin 2(\lambda -\lambda ^{\prime }) \big ] \bigg ] \bigg \vert _{\lambda _{1}}^{\lambda _{2}} \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&= G \rho \int _{r_{1}}^{r_{2}} \int _{\theta _{1}}^{\theta _{2}} \frac{ {r^{\prime }}^{2} \sin \theta ^{\prime } }{4 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{5} } \bigg [ - 6 {r^{\prime }}^{2} \sin ^2 \theta ^{\prime } \sin (\lambda _2 - \lambda _1 ) \cos (2 \lambda - \lambda _1 - \lambda _2) \\&\quad - (\lambda _2 - \lambda _1 ) (4 r^2 + {r^{\prime }}^{2} - 8 r r^{\prime } \cos \theta ^{\prime } + 3 {r^{\prime }}^{2} \cos 2 \theta ^{\prime } ) \bigg ] \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&= G \rho \int _{r_{1}}^{r_{2}} \bigg \{ \frac{r^{\prime }}{8 r^3 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta ^{\prime }}\big )^{3}} \bigg [ r r^{\prime } \Big [ 8 (r^2 + 3 {r^{\prime }}^{2} ) (\lambda _2 - \lambda _1) \cos \theta ^{\prime } \\&\quad - 3 r r^{\prime } \cos 2 \theta ^{\prime } \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2 (\lambda - \lambda _1) + \sin 2 (\lambda - \lambda _2) \big ] \Big ] \\&+ 2 \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 4r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 - 12 r r^{\prime } (r^2 + {r^{\prime }}^2) \cos \theta ^{\prime } \big ] \\&\quad -2 {r^{\prime }}^2 (9 r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1) \bigg ] \bigg \} \bigg \vert _{\theta _{1}}^{\theta _{2}} \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(55)

where in Eq. (55),

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} \frac{r^{\prime }}{8 r^3 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2}\big )^{3}} \bigg [ r r^{\prime } \Big [ 8 (r^2 + 3 {r^{\prime }}^{2} ) (\lambda _2 - \lambda _1) \cos \theta _2 \\&\quad - 3 r r^{\prime } \cos 2 \theta _2 \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2 (\lambda - \lambda _1) + \sin 2 (\lambda - \lambda _2) \big ] \Big ] \\&\quad + 2 \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 4r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 - 12 r r^{\prime } (r^2 + {r^{\prime }}^2) \cos \theta _2 \big ] \\&\quad -2 {r^{\prime }}^2 (9 r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1) \bigg ] \textrm{d} r^{\prime } \\&\quad = \frac{1}{48} \bigg [ - 3 \cos \theta _2 \big [ 8 (\lambda _2 - \lambda _1 ) \sin ^2 \theta _2 \\&\quad - 4 \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) (5-\cos 2 \theta _2) \big ] \ln \Big ( r^{\prime } - r \cos \theta _2 + \sqrt{r^2 + {r^{\prime }}^2 - 2 r r^{\prime } \cos \theta _2 } \Big ) \\&\quad + \frac{1}{r^3 \sqrt{r^2 + {r^{\prime }}^2 - 2 r r^{\prime } \cos \theta _2 }} \Big [ -4 (r^4 + r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 ) (\lambda _2 - \lambda _1) \\&\quad + 2 r^2 \big [ (3r^2 + {r^{\prime }}^2 ) \cos 2 \theta _2 - 3 r r^{\prime } \cos 3 \theta _2 \big ] \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2(\lambda - \lambda _1) + \sin 2(\lambda - \lambda _2) \big ] \\&\quad + 4 (13 r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 ) \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1 ) \\&\quad + 4 r r^{\prime } \cos \theta _2 \big [ (r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1 )- (25r^2 + 4 {r^{\prime }}^2) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ] \Big ] \bigg ] \bigg \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(56)

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} - \frac{r^{\prime }}{8 r^3 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1}\big )^{3}} \bigg [ r r^{\prime } \Big [ 8 (r^2 + 3 {r^{\prime }}^{2} ) (\lambda _2 - \lambda _1) \cos \theta _1 \\&\quad - 3 r r^{\prime } \cos 2 \theta _1 \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2 (\lambda - \lambda _1) + \sin 2 (\lambda - \lambda _2) \big ] \Big ] \\&\quad + 2 \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 4r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 - 12 r r^{\prime } (r^2 + {r^{\prime }}^2) \cos \theta _1 \big ] \\&\quad -2 {r^{\prime }}^2 (9 r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1) \bigg ] \textrm{d} r^{\prime } \\&\quad = - \frac{1}{48} \bigg [ - 3 \cos \theta _1 \big [ 8 (\lambda _2 - \lambda _1 ) \sin ^2 \theta _1 \\&\quad - 4 \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) (5-\cos 2 \theta _1) \big ] \ln \Big ( r^{\prime } - r \cos \theta _1 + \sqrt{r^2 + {r^{\prime }}^2 - 2 r r^{\prime } \cos \theta _1 } \Big ) \\&\quad + \frac{1}{r^3 \sqrt{r^2 + {r^{\prime }}^2 - 2 r r^{\prime } \cos \theta _1 }} \Big [ -4 (r^4 + r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 ) (\lambda _2 - \lambda _1) \\&\quad + 2 r^2 \big [ (3r^2 + {r^{\prime }}^2 ) \cos 2 \theta _1 - 3 r r^{\prime } \cos 3 \theta _1 \big ] \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2(\lambda - \lambda _1) + \sin 2(\lambda - \lambda _2) \big ] \\&\quad + 4 (13 r^4 + 13 r^2 {r^{\prime }}^2 + 4 {r^{\prime }}^4 ) \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1 ) \\&\quad + 4 r r^{\prime } \cos \theta _1 \big [ (r^2 + 4 {r^{\prime }}^2 ) (\lambda _2 - \lambda _1 )- (25r^2 + 4 {r^{\prime }}^2) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ] \Big ] \bigg ] \bigg \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(57)

After substituting Eqs. (56) and (57) into Eq. (55), the analytical expression for the $V_{yy}$ of a tesseroid is obtained in Eq. (15).

The other GGT components $V_{xy}$, $V_{xz}$, and $V_{yz}$ of a tesseroid are derived and presented in the Mathematica code GGT_VxyVxzVyz.nb at the link https://github.com/xiaoledeng/analytical-tesseroid-spherical-zonal-band.

Appendix D

Derivation of the Analytical Expressions for the GC of a Tesseroid

Table 13 Detailed expressions for the $O_{22}$, $O_{12}$, $O_{21}$, and $O_{11}$ for the $V_{rrr}$ in Eq. (17)

Table 14 Detailed expressions for the $P_{22}$, $P_{12}$, $P_{21}$, $P_{11}$, $Q_{22}$, $Q_{12}$, $Q_{21}$, $Q_{11}$, $R_{22}$, $R_{12}$, $R_{21}$, $R_{11}$, $S_{22}$, $S_{12}$, $S_{21}$, $S_{11}$, $T_{2}$, and $T_{1}$ for the $V_{xxz}$ in Eq. (20)

Table 15 Detailed expressions for the $V_{22}$, $V_{12}$, $V_{21}$, $V_{11}$, $W_{22}$, $W_{12}$, $W_{21}$, and $W_{11}$ for the $V_{yyz}$ in Eq. (21), where the expressions for the $U_{22}$, $U_{12}$, $U_{21}$, and $U_{11}$ are referred to in Table 14

When the computation point P is located on the polar axis with its colatitude $\theta =0$, substituting Eqs. (39), (43) and (44) into Eq. (16) yields:

$$\begin{aligned} \begin{aligned}&{V_{rrr} } = G \rho \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{l_{1}}^{l_{2}} {r^{\prime }}^{2} \Big [ \frac{15}{l^{7}} (- \frac{l^2+r^2-{r^{\prime }}^{2}}{2 r})^{3} - \frac{9}{l^{5}} (- \frac{l^2+r^2-{r^{\prime }}^{2}}{2 r}) \Big ] \frac{l}{r r^{\prime }} \textrm{d} l \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&\quad = \frac{3 G \rho }{8 r^4} \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} \int _{l_{1}}^{l_{2}} \frac{r^{\prime } (l^2+r^2-{r^{\prime }}^{2}) \big [ 12 l^2 r^2 - 5 (l^2 + r^2 -{r^{\prime }}^{2})^2 \big ] }{l^6} \textrm{d} l \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&\quad = \frac{3 G \rho }{8 r^4} \int _{r_{1}}^{r_{2}} \int _{\lambda _{1}}^{\lambda _{2}} r^{\prime } \Big [ -5 l + \frac{3(r^{2} - 5 {r^{\prime }}^{2})}{l} + \frac{r^{4} - 6 r^{2} {r^{\prime }}^{2} + 5 {r^{\prime }}^{4} }{l^{3}} + \frac{(r^{2} - {r^{\prime }}^{2} )^{3}}{l^{5}} \Big ] \Big \vert _{l_{1}}^{l_{2}} \textrm{d} \lambda ^{\prime } \textrm{d} r^{\prime } \\&\quad = \frac{3 G \rho (\lambda _2 - \lambda _1)}{8 r^4} \int _{r_{1}}^{r_{2}} \Big \{ r^{\prime } \Big [ -5 l_{2} + \frac{3(r^{2} - 5 {r^{\prime }}^{2})}{l_{2}} + \frac{r^{4} - 6 r^{2} {r^{\prime }}^{2} + 5 {r^{\prime }}^{4} }{{l_{2}}^{3}} + \frac{(r^{2} - {r^{\prime }}^{2} )^{3}}{{l_{2}}^{5}} \Big ] \\&\quad - r^{\prime } \Big [ -5 l_{1} + \frac{3(r^{2} - 5 {r^{\prime }}^{2})}{l_{1}} + \frac{r^{4} - 6 r^{2} {r^{\prime }}^{2} + 5 {r^{\prime }}^{4} }{{l_{1}}^{3}} + \frac{(r^{2} - {r^{\prime }}^{2} )^{3}}{{l_{1}}^{5}} \Big ] \Big \} \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(58)

In Eq. (58), $\begin{aligned} \int _{r_{1}}^{r_{2}} r^{\prime } \Big [ -5 l_{2} + \frac{3(r^{2} - 5 {r^{\prime }}^{2})}{l_{2}} + \frac{r^{4} - 6 r^{2} {r^{\prime }}^{2} + 5 {r^{\prime }}^{4} }{{l_{2}}^{3}} + \frac{(r^{2} - {r^{\prime }}^{2} )^{3}}{{l_{2}}^{5}} \Big ] \textrm{d} r^{\prime } \end{aligned}$ is obtained as:

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} r^{\prime } \Big [ -5 \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2} + \frac{3(r^{2} - 5 {r^{\prime }}^{2})}{\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2}} \\&\quad + \frac{r^{4} - 6 r^{2} {r^{\prime }}^{2} + 5 {r^{\prime }}^{4} }{\big ( \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2} \big )^{3}} + \frac{(r^{2} - {r^{\prime }}^{2} )^{3}}{\big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2}\big )^{5}} \Big ] \textrm{d} r^{\prime } \\&\quad = - \frac{4 {r^{\prime }}^{3} \big [ 9 r^2 r^{\prime } + 4 {r^{\prime }}^{3} - 4 r (r^2 + 3 {r^{\prime }}^{2} ) \cos \theta _2 + 3 r^2 r^{\prime } \cos 2 \theta _2 \big ] }{3 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _2} \big )^{3}} \Big \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(59)

and $\begin{aligned} \int _{r_{1}}^{r_{2}} - r^{\prime } \Big [ -5 l_{1} + \frac{3(r^{2} - 5 {r^{\prime }}^{2})}{l_{1}} + \frac{r^{4} - 6 r^{2} {r^{\prime }}^{2} + 5 {r^{\prime }}^{4} }{{l_{1}}^{3}} + \frac{(r^{2} - {r^{\prime }}^{2} )^{3}}{{l_{1}}^{5}} \Big ] \textrm{d} r^{\prime } \end{aligned}$ is obtained as:

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} - r^{\prime } \Big [ -5 \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1} + \frac{3(r^{2} - 5 {r^{\prime }}^{2})}{\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1}} \\&\quad + \frac{r^{4} - 6 r^{2} {r^{\prime }}^{2} + 5 {r^{\prime }}^{4} }{\big ( \sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1} \big )^{3}} + \frac{(r^{2} - {r^{\prime }}^{2} )^{3}}{\big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1}\big ) ^{5}} \Big ] \textrm{d} r^{\prime } \\&\quad = \frac{4 {r^{\prime }}^{3} \big [ 9 r^2 r^{\prime } + 4 {r^{\prime }}^{3} - 4 r (r^2 + 3 {r^{\prime }}^{2} ) \cos \theta _1 + 3 r^2 r^{\prime } \cos 2 \theta _1 \big ] }{3 \big (\sqrt{r^{2} + {r^{\prime }}^{2} - 2 r r^{\prime } \cos \theta _1} \big )^{3}} \Big \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(60)

After substituting Eqs. (59) and (60) into Eq. (58), the analytical expression for the radial-radial-radial GC of a tesseroid when the computation point is located on the polar axis is obtained in Eq. (17).

Regarding the analytical expression for the $V_{xxz}$ of a tesseroid with the colatitude of the computation point $\theta = 0$, substituting Eqs. (37), (43) and (51) into Eq. (18) yields:

$$\begin{aligned} \begin{aligned}&V_{xxz} = G \rho \int _{r_{1}}^{r_{2}} \int _{\theta _{1}}^{\theta _{2}} \int _{\lambda _{1}}^{\lambda _{2}} {r^{\prime }}^{2} \Big [ \frac{15 [- r^{\prime } \sin \theta ^{\prime } \cos (\lambda ^{\prime } - \lambda )]^2 (r^{\prime } \cos \theta ^{\prime } -r) }{l^{7}} \\&\quad - \frac{3 (r^{\prime } \cos \theta ^{\prime } -r) }{l^{5}} \Big ] \sin \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&\quad = G \rho \int _{r_{1}}^{r_{2}}\int _{\theta _{1}}^{\theta _{2}} \frac{3 {r^{\prime }}^2 (r-r^{\prime } \cos \theta ^{\prime }) \sin \theta ^{\prime }}{4 \big (\sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime }} \big )^7} \Big [ 4 (r^2 + {r^{\prime }}^2) \lambda ^{\prime } - 8 r r^{\prime } \cos \theta ^{\prime } \lambda ^{\prime } \\&\quad + 5 {r^{\prime }}^2 \sin ^2 \theta ^{\prime } \big [ 2 \lambda - 2 \lambda ^{\prime } + \sin 2 (\lambda - \lambda ^{\prime }) \big ] \Big ] \Big \vert _{\lambda _{1}}^{\lambda _{2}} \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&\quad = G \rho \int _{r_{1}}^{r_{2}}\int _{\theta _{1}}^{\theta _{2}} \frac{3 {r^{\prime }}^2 (r-r^{\prime } \cos \theta ^{\prime }) \sin \theta ^{\prime }}{4 \big (\sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime }} \big )^7} \Big [ (\lambda _2 - \lambda _1) (4r^2 - {r^{\prime }}^2 - 8 r r^{\prime } \cos \theta ^{\prime } + 5 {r^{\prime }}^2 \cos 2 \theta ^{\prime } ) \\&\quad - 10 {r^{\prime }}^2 \sin ^2 \theta ^{\prime } \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) \Big ] \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&\quad = G \rho \int _{r_{1}}^{r_{2}} \bigg \{ -\frac{r^{\prime }}{32r^4 \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime }}}\bigg [ 18 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \\&\quad + \frac{3 (r^2 - {r^{\prime }}^2 )^3 \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2(\lambda - \lambda _1) - \sin 2 (\lambda - \lambda _2) \big ]}{(r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime } )^2} \\&\quad + \frac{(r^2 - {r^{\prime }}^2) \big [6 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) - 10(r^2 + 3 {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ]}{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime }} \\&\quad - 15 (r^2 + {r^{\prime }}^2) \sqrt{1- \frac{2r r^{\prime } \cos \theta ^{\prime }}{r^2 + {r^{\prime }}^2}} \left( \sqrt{1- \frac{2r r^{\prime } \cos \theta ^{\prime }}{r^2 + {r^{\prime }}^2} } - 1 \right) \Big [ 2\lambda _2 - 2\lambda _1 \\&\quad + \sin 2(\lambda -\lambda _1) - \sin 2 (\lambda - \lambda _2)\Big ] - 30 (r^2 + 3 {r^{\prime }}^2 ) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \bigg ] \bigg \} \bigg \vert _{\theta _{1}}^{\theta _{2}} \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(61)

where in Eq. (61),

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} -\frac{r^{\prime }}{32r^4 \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _2}}\bigg [ 18 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \\&\quad + \frac{3 (r^2 - {r^{\prime }}^2 )^3 \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2(\lambda - \lambda _1) - \sin 2 (\lambda - \lambda _2) \big ]}{(r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _2 )^2} \\&\quad + \frac{(r^2 - {r^{\prime }}^2) \big [6 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) - 10(r^2 + 3 {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ]}{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _2} \\&\quad - 15 (r^2 + {r^{\prime }}^2) \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} \left( \sqrt{1- \frac{2r r^{\prime } \cos \theta _2 }{r^2 + {r^{\prime }}^2}} - 1 \right) \Big [ 2\lambda _2 - 2\lambda _1 \\&\quad + \sin 2(\lambda -\lambda _1) - \sin 2 (\lambda - \lambda _2)\Big ] - 30 (r^2 + 3 {r^{\prime }}^2 ) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \bigg ] \textrm{d} r^{\prime } \\&\quad = \frac{1}{16 r^4 \big ( \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _2} \big )^3 } \bigg [ 6 r^2 {r^{\prime }}^4 \cos 2 \theta _2 \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2(\lambda - \lambda _1) - \sin 2(\lambda - \lambda _2) \big ] \\&\quad - \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) \Big [ 5 r^6 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} + {r^{\prime }}^6 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} -16\right) \\&\quad + r^2 {r^{\prime }}^4 \left( 15 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} -52\right) + r^4 {r^{\prime }}^2 \left( 15 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} - 16 \right) \Big ] \\&\quad + 2 r r^{\prime } \cos \theta _2 \Big [ (\lambda _2 - \lambda _1) \big [ 5 r^4 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} \\&\quad + {r^{\prime }}^4 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} - 24 \right) + 2 r^2 {r^{\prime }}^2 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} - 4 \right) \big ] \\&+ (r^2 + {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 5 r^2 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} \\&\quad + {r^{\prime }}^2 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} - 24 \right) \big ] \Big ] \\&- 5 (r^2 + {r^{\prime }}^2)^3 (\lambda _2 - \lambda _1) \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} + 4 {r^{\prime }}^4 (9r^2 + 4 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \bigg ] \bigg \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(62)

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} \frac{r^{\prime }}{32r^4 \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _1}}\bigg [ 18 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \\&\quad + \frac{3 (r^2 - {r^{\prime }}^2 )^3 \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2(\lambda - \lambda _1) - \sin 2 (\lambda - \lambda _2) \big ]}{(r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _1 )^2} \\&\quad + \frac{(r^2 - {r^{\prime }}^2) \big [6 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) - 10(r^2 + 3 {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ]}{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _1} \\&\quad - 15 (r^2 + {r^{\prime }}^2) \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} \left( \sqrt{1- \frac{2r r^{\prime } \cos \theta _1 }{r^2 + {r^{\prime }}^2}} - 1 \right) \Big [ 2\lambda _2 - 2\lambda _1 \\&\quad + \sin 2(\lambda -\lambda _1) - \sin 2 (\lambda - \lambda _2)\Big ] - 30 (r^2 + 3 {r^{\prime }}^2 ) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \bigg ] \textrm{d} r^{\prime } \\&\quad = - \frac{1}{16 r^4 \big ( \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _1} \big )^3 } \bigg [ 6 r^2 {r^{\prime }}^4 \cos 2 \theta _1 \big [ 2 \lambda _2 - 2 \lambda _1 + \sin 2(\lambda - \lambda _1) - \sin 2(\lambda - \lambda _2) \big ] \\&\quad - \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) \Big [ 5 r^6 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} + {r^{\prime }}^6 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} -16 \right) \\&\quad + r^2 {r^{\prime }}^4 \left( 15 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} -52\right) + r^4 {r^{\prime }}^2 \left( 15 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} - 16 \right) \Big ] \\&\quad + 2 r r^{\prime } \cos \theta _1 \Big [ (\lambda _2 - \lambda _1) \big [ 5 r^4 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} + {r^{\prime }}^4 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} - 24 \right) \\&\quad + 2 r^2 {r^{\prime }}^2 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} - 4 \right) \big ] \\&\quad + (r^2 + {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 5 r^2 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} \\&\quad + {r^{\prime }}^2 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} - 24 \right) \big ] \Big ] \\&\quad - 5 (r^2 + {r^{\prime }}^2)^3 (\lambda _2 - \lambda _1) \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} + 4 {r^{\prime }}^4 (9r^2 + 4 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \bigg ] \bigg \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(63)

After substituting Eqs. (62) and (63) into Eq. (61), the analytical expression for the $V_{xxz}$ of a tesseroid is obtained in Eq. (20).

Moreover, substituting Eqs. (13), (37), and (43) into Eq. (19) yields the expression for the $V_{yyz}$ of a tesseroid with the colatitude of the computation point $\theta = 0$ as:

$$\begin{aligned} \begin{aligned}&V_{yyz} = G \rho \int _{r_{1}}^{r_{2}} \int _{\theta _{1}}^{\theta _{2}} \int _{\lambda _{1}}^{\lambda _{2}} {r^{\prime }}^{2} \Big [ \frac{15 [r^{\prime } \sin \theta ^{\prime } \sin (\lambda ^{\prime }-\lambda )]^2 (r^{\prime } \cos \theta ^{\prime } -r) }{l^{7}} \\&\quad - \frac{3 (r^{\prime } \cos \theta ^{\prime } -r) }{l^{5}} \Big ] \sin \theta ^{\prime } \textrm{d} \lambda ^{\prime } \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&\quad = G \rho \int _{r_{1}}^{r_{2}}\int _{\theta _{1}}^{\theta _{2}} \frac{3 {r^{\prime }}^2 (r-r^{\prime } \cos \theta ^{\prime }) \sin \theta ^{\prime }}{4 \big (\sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime }} \big )^7} \Big [ 4 (r^2 + {r^{\prime }}^2) \lambda ^{\prime } - 8 r r^{\prime } \cos \theta ^{\prime } \lambda ^{\prime } \\&\quad + 5 {r^{\prime }}^2 \sin ^2 \theta ^{\prime } \big [ 2 \lambda - 2 \lambda ^{\prime } - \sin 2 (\lambda - \lambda ^{\prime }) \big ] \Big ] \Big \vert _{\lambda _{1}}^{\lambda _{2}} \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&\quad = G \rho \int _{r_{1}}^{r_{2}}\int _{\theta _{1}}^{\theta _{2}} \frac{3 {r^{\prime }}^2 (r-r^{\prime } \cos \theta ^{\prime }) \sin \theta ^{\prime }}{4 \big (\sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime }} \big )^7} \Big [ (\lambda _2 - \lambda _1) (4r^2 - {r^{\prime }}^2 - 8 r r^{\prime } \cos \theta ^{\prime } + 5 {r^{\prime }}^2 \cos 2 \theta ^{\prime } ) \\&\quad + 10 {r^{\prime }}^2 \sin ^2 \theta ^{\prime } \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) \Big ] \textrm{d} \theta ^{\prime } \textrm{d} r^{\prime } \\&\quad = G \rho \int _{r_{1}}^{r_{2}} \bigg \{ -\frac{r^{\prime }}{32r^4 \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime }}}\bigg [ 18 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \\&\quad + \frac{3 (r^2 - {r^{\prime }}^2 )^3 \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2(\lambda - \lambda _1) + \sin 2 (\lambda - \lambda _2) \big ]}{(r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime } )^2} \\&\quad + \frac{(r^2 - {r^{\prime }}^2) \big [6 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) + 10(r^2 + 3 {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ]}{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta ^{\prime }} \\&\quad - 15 (r^2 + {r^{\prime }}^2) \sqrt{1- \frac{2r r^{\prime } \cos \theta ^{\prime }}{r^2 + {r^{\prime }}^2}} \left( \sqrt{1- \frac{2r r^{\prime } \cos \theta ^{\prime }}{r^2 + {r^{\prime }}^2} } - 1 \right) \Big [ 2\lambda _2 - 2\lambda _1 \\&\quad - \sin 2(\lambda -\lambda _1) + \sin 2 (\lambda - \lambda _2)\Big ] + 30 (r^2 + 3 {r^{\prime }}^2 ) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \bigg ] \bigg \} \bigg \vert _{\theta _{1}}^{\theta _{2}} \textrm{d} r^{\prime } \end{aligned} \end{aligned}$$

(64)

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} -\frac{r^{\prime }}{32r^4 \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _2}}\bigg [ 18 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \\&\quad + \frac{3 (r^2 - {r^{\prime }}^2 )^3 \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2(\lambda - \lambda _1) + \sin 2 (\lambda - \lambda _2) \big ]}{(r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _2 )^2} \\&\quad + \frac{(r^2 - {r^{\prime }}^2) \big [6 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) + 10(r^2 + 3 {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ]}{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _2} \\&\quad - 15 (r^2 + {r^{\prime }}^2) \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} \left( \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2} } - 1 \right) \Big [ 2\lambda _2 - 2\lambda _1 \\&\quad - \sin 2(\lambda -\lambda _1) + \sin 2 (\lambda - \lambda _2)\Big ] + 30 (r^2 + 3 {r^{\prime }}^2 ) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \bigg ] \textrm{d} r^{\prime } \\&\quad = \frac{1}{16 r^4 \big ( \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _2} \big )^3 } \bigg [ 6 r^2 {r^{\prime }}^4 \cos 2 \theta _2 \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2(\lambda - \lambda _1) + \sin 2(\lambda - \lambda _2) \big ] \\&\quad + \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) \Big [ 5 r^6 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} + {r^{\prime }}^6 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} -16 \right) \\&\quad + r^2 {r^{\prime }}^4 \left( 15 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} -52\right) + r^4 {r^{\prime }}^2 \left( 15 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} - 16 \right) \Big ] \\&\quad + 2 r r^{\prime } \cos \theta _2 \Big [ (\lambda _2 - \lambda _1) \big [ 5 r^4 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} + {r^{\prime }}^4 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} - 24 \right) \\&\quad + 2 r^2 {r^{\prime }}^2 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} - 4 \right) \big ] \\&\quad - (r^2 + {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 5 r^2 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} \\&\quad + {r^{\prime }}^2 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} - 24 \right) \big ] \Big ] \\&\quad - 5 (r^2 + {r^{\prime }}^2)^3 (\lambda _2 - \lambda _1) \sqrt{1- \frac{2r r^{\prime } \cos \theta _2}{r^2 + {r^{\prime }}^2}} + 4 {r^{\prime }}^4 (9r^2 + 4 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \bigg ] \bigg \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(65)

$$\begin{aligned} \begin{aligned}&\int _{r_{1}}^{r_{2}} \frac{r^{\prime }}{32r^4 \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _1}}\bigg [ 18 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \\&\quad + \frac{3 (r^2 - {r^{\prime }}^2 )^3 \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2(\lambda - \lambda _1) + \sin 2 (\lambda - \lambda _2) \big ]}{(r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _1 )^2} \\&\quad + \frac{(r^2 - {r^{\prime }}^2) \big [6 (r^2 - 5 {r^{\prime }}^2) (\lambda _2 - \lambda _1) + 10(r^2 + 3 {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big ]}{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _1} \\&\quad - 15 (r^2 + {r^{\prime }}^2) \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} \left( \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2} } - 1 \right) \Big [ 2\lambda _2 - 2\lambda _1 \\&\quad - \sin 2(\lambda -\lambda _1) + \sin 2 (\lambda - \lambda _2)\Big ] + 30 (r^2 + 3 {r^{\prime }}^2 ) \cos (2 \lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \bigg ] \textrm{d} r^{\prime } \\&\quad = - \frac{1}{16 r^4 \big ( \sqrt{r^2 + {r^{\prime }}^2 -2 r r^{\prime } \cos \theta _1} \big )^3 } \bigg [ 6 r^2 {r^{\prime }}^4 \cos 2 \theta _1 \big [ 2 \lambda _2 - 2 \lambda _1 - \sin 2(\lambda - \lambda _1) + \sin 2(\lambda - \lambda _2) \big ] \\&\quad + \cos (2 \lambda - \lambda _1 - \lambda _2 ) \sin (\lambda _2 - \lambda _1) \Big [ 5 r^6 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} + {r^{\prime }}^6 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} -16 \right) \\&\quad + r^2 {r^{\prime }}^4 \left( 15 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} -52\right) + r^4 {r^{\prime }}^2 \left( 15 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} - 16 \right) \Big ] \\&\quad + 2 r r^{\prime } \cos \theta _1 \Big [ (\lambda _2 - \lambda _1) \big [ 5 r^4 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} + {r^{\prime }}^4 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} - 24 \right) \\&\quad + 2 r^2 {r^{\prime }}^2 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} - 4 \right) \big ] \\&\quad - (r^2 + {r^{\prime }}^2) \cos (2\lambda - \lambda _1 - \lambda _2) \sin (\lambda _2 - \lambda _1) \big [ 5 r^2 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}}\\&\quad + {r^{\prime }}^2 \left( 5 \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} - 24 \right) \big ] \Big ] \\&\quad - 5 (r^2 + {r^{\prime }}^2)^3 (\lambda _2 - \lambda _1) \sqrt{1- \frac{2r r^{\prime } \cos \theta _1}{r^2 + {r^{\prime }}^2}} + 4 {r^{\prime }}^4 (9r^2 + 4 {r^{\prime }}^2) (\lambda _2 - \lambda _1) \bigg ] \bigg \vert _{r_{1}}^{r_{2}} \end{aligned} \end{aligned}$$

(66)

After substituting Eqs. (65) and (66) into Eq. (64), the analytical formula of the $V_{yyz}$ is obtained in Eq. (21).

Regarding other GC components ($V_{xxx}$, $V_{xxy}$, $V_{xyz}$, $V_{yyx}$, $V_{yyy}$, $V_{zzx}$, and $V_{zzy}$) of a tesseroid, their derivation progresses are presented in the Mathematica code GC_VxxxVxxyVxyzVyyxVyyyVzzxVzzy.nb at the link https://github.com/xiaoledeng/analytical-tesseroid-spherical-zonal-band.

Appendix E

Laplace’s Equation for the GGT and GC of a Tesseroid and Spherical Zonal Band

Regarding the expressions for the ${V_{xxz}}^{\textrm{zb}}$ and ${V_{yyz}}^{\textrm{zb}}$ of a spherical zonal band in Eq. (27), the within expressions for the $X_{22}$, $X_{12}$, $X_{21}$, $X_{11}$, $Y_{22}$, $Y_{12}$, $Y_{21}$, $Y_{11}$, $Z_{22}$, $Z_{12}$, $Z_{21}$, and $Z_{11}$ are presented in Table 16.

Table 16 Detailed expressions for the $X_{22}$, $X_{12}$, $X_{21}$, $X_{11}$, $Y_{22}$, $Y_{12}$, $Y_{21}$, $Y_{11}$, $Z_{22}$, $Z_{12}$, $Z_{21}$, and $Z_{11}$ for the ${V_{xxz}}^{\textrm{zb}}$ and ${V_{yyz}}^{\textrm{zb}}$ in Eq. (27), where the expressions for the $U_{22}$, $U_{12}$, $U_{21}$, and $U_{11}$ are referred to in Table 14

In this study, the correctness of the analytical expressions for the GGT and GC of a tesseroid and spherical zonal band is confirmed by using Laplace’s equation. In detail, Laplace’s equations for the GGT and GC of a tesseroid and spherical zonal band can be presented as:

$$\begin{aligned}{} & {} V_{xx} + V_{yy} + V_{zz} = 0 \end{aligned}$$

(67)

$$\begin{aligned}{} & {} V_{xxz} + V_{yyz} + V_{zzz} = 0 \end{aligned}$$

(68)

$$\begin{aligned}{} & {} {V_{xx}}^{\textrm{zb}} + {V_{yy}}^{\textrm{zb}} + {V_{zz}}^{\textrm{zb}} = 0 \end{aligned}$$

(69)

$$\begin{aligned}{} & {} {V_{xxz}}^{\textrm{zb}} + {V_{yyz}}^{\textrm{zb}} + {V_{zzz}}^{\textrm{zb}} = 0 \end{aligned}$$

(70)

Theoretically, the expressions for the $V_{xx}$ in Eq. (14), $V_{yy}$ in Eq. (15), and $V_{zz}$ in Eq. (9); $V_{xxz}$ in Eq. (20), $V_{yyz}$ in Eq. (21), and $V_{zzz}$ in Eq. (17); ${V_{xx}}^{\textrm{zb}}$ in Eq. (25), ${V_{yy}}^{\textrm{zb}}$ in Eq. (25), and ${V_{zz}}^{\textrm{zb}}$ in Eq. (24); ${V_{xxz}}^{\textrm{zb}}$ in Eq. (27), ${V_{yyz}}^{\textrm{zb}}$ in Eq. (27), and ${V_{zzz}}^{\textrm{zb}}$ in Eq. (26) satisfy the above Laplace’s equations in Eqs. (67), (68), (69), and (70), respectively. These processes are presented in the Mathematica code (AppendixE.nb) at https://github.com/xiaoledeng/analytical-tesseroid-spherical-zonal-band, in which the sums of three quantities (i.e., $V_{xx}$, $V_{yy}$, and $V_{zz}$; $V_{xxz}$, $V_{yyz}$, and $V_{zzz}$; ${V_{xx}}^{\textrm{zb}}$, ${V_{yy}}^{\textrm{zb}}$, and ${V_{zz}}^{\textrm{zb}}$; ${V_{xxz}}^{\textrm{zb}}$, ${V_{yyz}}^{\textrm{zb}}$, and ${V_{zzz}}^{\textrm{zb}}$) are equal to zero.

Appendix F

Consistency of the Analytical Expressions for Gravitational Effects of a Spherical Zonal Band Between Deng (2022) and this Paper

The old formulas of the GP, radial GV, radial-radial GGT, and radial-radial-radial GC of a spherical zonal band can be obtained by substituting Eqs. (3), (5), (7), and (9) in Deng (2022) into Eq. (18) in Deng (2022). The new formulas of the GP, radial GV, radial-radial GGT, and radial-radial-radial GC of a spherical zonal band are derived in Eqs. (22), (23), (24), and (26) in this paper. It can be seen that these new formulas are simpler in forms and more intuitive in methods than the old ones.

To reveal the consistency between the new and old formulas of the gravitational effects of a spherical zonal band, the Mathematica code (AppendixF.nb) is provided at https://github.com/xiaoledeng/analytical-tesseroid-spherical-zonal-band. In the AppendixF.nb, the analytical differences between the new and old formulas of the GP, radial GV, radial-radial GGT, and radial-radial-radial GC of a spherical zonal band are equal to zero, which confirms the consistency of the analytical expressions.