1 Introduction

Real shell structures are very often characterized by irregular geometry, Fig. 1, discontinuous material properties, loadings, deformations, and boundary conditions. Junctions in shell structures were considered in many books and articles; some review of this literature is presented in the paper [34] and in the references of the publications cited therein.

Fig. 1
figure 1

Irregular shell structures

Full size image

In this work, we use the exact shell theory proposed by Reissner [35, 36]. He noted that the nonlinear theory of regular shells could be formulated by direct through-the-thickness integration of the 3D equilibrium conditions of continuum mechanics. This approach was developed by Libai and Simmonds [20, 21]. They presented the general, dynamically, and kinematically exact, six-scalar-field theory of regular shells, formulated on the non-material surface as the shell base surface. The kinematics of the shell is modelled by six degrees of freedom, three translations, and three rotations.

The description of an irregular shell within the exact nonlinear shell theory was initiated by Makowski and Stumpf [23], and the jump conditions along the junction in a thin irregular shell structure have been presented in [22]. This approach was developed to consider the connection of regular shell elements of any thickness in the book [6], but the authors assumed that the region of shell irregularity is small as compared with other shell dimensions and its size can be ignored in deriving the resultant 2D equilibrium conditions. The exact, resultant continuity conditions along the singular curve modelling the junction for two classes of irregular shell structures, such as the branching shell and the self-intersecting shell, are presented in the paper [18]. In that work, the real dimensions and geometry of the branching and self-intersecting regions of complex shell structures are taken into account in the through-the-thickness integration process. Article [33] presented the unique 2D kinematic relations, which are work-conjugated to the exact, resultant local equilibrium conditions of the nonlinear theory of branching shells. This kinematics corresponds to the two-dimensional Cosserat continuum described by independent translation and rotation fields, see [1, 8].

An analytical solution to the problem of reinforcement in a junction of an irregular shell structure can be found in Chapter 16 of the book [29]; however, the authors have limited their considerations to the linear theory of thin shells. The paper [19] considers the problem of an elastic cylindrical shell connected to a circular plate with reinforcement along the junction. Starting from the six-parameter shell theory, small axially symmetric deformations are described. Other approaches are also known in the literature, for example, in [15] where buckling and optimal design of ring-stiffened thin cylindrical shells are considered, and in [5] where the problem of free and forced vibration of ring-stiffened conical-cylindrical shells is presented.

The numerical analysis of shells stiffened with beams using geometrically exact theories of shells and beams is presented in the paper [4]. The author presents the FEM solution of many interesting examples of static and stability linear analyses and novel design formulas for the stability of stiffened shells. The kinematical relations for shell and beam are described by the Cosserat surface and Cosserat rod, respectively. The paper [25] presents the use of the nonlinear theory of Cosserat rods and the resulting finite element computer code for analyses of statics and dynamics of engineering structures to be applied in an advanced structural health monitoring system. In the literature, many papers are devoted to the problem of statics and stability of plates and shells stiffened with beams. Among the many publications, one can distinguish review papers by Mukhopadhyay and Mukherjee [28], Sinha and Mukhopadhyay [40], Bedair [3], and Ojeda and co-workers [30].

In this paper, we consider the irregular shell to consist of two regular elements reinforced by a beam along the junction. The 1D equilibrium equations along the beam axis derived by direct integration of the mechanical balance laws of continuum mechanics over beam cross section were formulated by Smoleński in [41]. The kinematics of reinforced junction is described by the Cosserat curve model which is kinematically consistent with the general shell theory [1, 8]. The 1D resultant beam model coincides with the Cosserat curve model discussed, for example, in Antman’s book [2]. Here, starting from 3D global equilibrium conditions of continuum mechanics by performing a direct integration procedure the 2D equilibrium conditions defined at the shell base surface and 1D equilibrium conditions defined along surface curve modelling reinforced junction are derived. The presented local continuity conditions along the singular curve take into account the real dimensions of the junction region and the beam cross section as well as their individual material properties.

2 General shell theory

2.1 3D shell-like body

Let us consider a shell as a three-dimensional solid body in which one dimension, called thickness is much smaller than the two others. This body in a reference (undeformed) placement is identified with region B of the physical space \({\mathcal {E}}\) where the 3D vector space E is translation space. The shell boundary \(\partial B\) consists of three parts: two shell faces, upper \(M^{+}\) and lower \(M^{-}\), and the lateral boundary surface \(\partial B^{*}\), then

$$\begin{aligned} \partial B=M^{+}\cup M^{-}\cup \partial B^{*},\quad M^{+}\cap M^{-}=\emptyset . \end{aligned}$$

The system of notation used here follows that of Libai and Simmonds [21] and Konopińska and Pietraszkiewicz [18].

The position vector \({{\textbf {x}}}\) of an arbitrary point \(\text {x}\in B\) can be described by

$$\begin{aligned} {{\textbf {x}}}{(}\theta ^{\alpha },\xi {)}={{\varvec{x}}}{(}\theta ^{\alpha }{)}+\xi \varvec{\eta }{(}\theta ^{\alpha }{)}, \end{aligned}$$
(1)

where \({{\varvec{x}}}{(}\theta ^{\alpha }{)}={{\textbf {x}}}{(}\theta ^{\alpha },0{)}\) is the position vector of a point x of some reference base surface M of the shell B, \(\theta ^{\alpha }\), \(\alpha =1,2\) are surface curvilinear coordinates on M, \(\xi \in {[}-h^{-},h^{+}{]}\) is the distance from M, and \(h=h^{-}+h^{+}\) is the shell thickness. Here \(\varvec{\eta }=\frac{1}{\sqrt{a}}{{\varvec{x}}},_{1}\times {{\varvec{x}}},_{2}\) is the unit normal vector of M, \(\times \) denotes a cross-product, \(a=\text {det}\left( {{\varvec{x}}},_{\alpha }\cdot {{\varvec{x}}},_{\beta }\right) \) and \((\dots ),_{\alpha }=\frac{\partial }{\partial \theta ^{\alpha }}(\dots )\) in an inertial frame \((o, {{\varvec{i}}}_{k})\) where \(o\in {\mathcal {E}}\) and \({{\varvec{i}}}_{k}\in E\), \(k=1,2,3\) are orthogonal vectors, see Fig. 2.

Fig. 2
figure 2

The geometry of the 3D shell-like body in the reference and deformed placements

Full size image

The position vector \({{\textbf {y}}}=\chi ({{\textbf {x}}})\) of the shell in the deformed placement \(\chi (B)\) is given by

$$\begin{aligned} {{\textbf {y}}}(\theta ^{\alpha },\xi )={{\varvec{y}}}(\theta ^{\alpha })+\varvec{\zeta }(\theta ^{\alpha },\xi ), \quad \varvec{\zeta }(\theta ^{\alpha },0)={{\textbf {0}}}, \end{aligned}$$
(2)

where \(\chi \) is deformation function, \({{\varvec{y}}}=\chi ({{\varvec{x}}})\) is the position vector of the deformed base surface \(\chi (M)\) and \(\varvec{\zeta }(\theta ^{\alpha },\xi )\) is a deviation of point y from the surface \(\chi (M)\).

In the referential description, the 3D global equilibrium equations are presented as vanishing of the total force \({{\textbf {F}}}(B)\) and torque \({{\textbf {T}}}_{\text {o}}(B)\) vectors taken relative to an arbitrary point of all forces acting on 3D shell-like body B

(3)

where \(\partial B_{f}\) is the part of boundary surface \(\partial B\) on which the traction vector field \({{\textbf {t}}}^{*}(\text {x})\) is prescribed, \({{\textbf {f}}}(\text {x})\) is the volume force vector field and \({{\textbf {t}}}_{n}(\text {x})\) is the contact force vector field. The traction vector \({{\textbf {t}}}^{*}(\text {x})\) can be prescribed on both shell faces \(M^{\pm }\) and on a part \(\partial B^{*}_{f}\) of the lateral boundary surface \(\partial B^{*}\).

2.2 Through-the-thickness integration

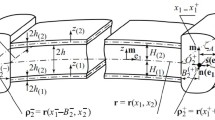
We consider two regular shell elements \(B_{1}\) and \(B_{2}\) connected along the common boundary. This connection is reinforced by a beam along the junction, see, for example, Fig. 3. Using the through-the-thickness integration procedure, the global equilibrium conditions (3) of regular shell element can be expressed through the resultant fields defined entirely on the reference base surface. In this work, we assume that the axis of reinforcement in a reference configuration \(\varGamma \) coincides with a common boundary of base surfaces \(M_{1}\) and \(M_{2}\).

Fig. 3
figure 3

During the direct integration procedure, some surface and volume fields in the junction region are integrated twice

Full size image

The total force vector of spatial forces acting in \(B_{1}\) and on boundary \(\partial B_{1}\) defined on the base surface is given by

(4)

where \(\partial M\) is the boundary of shell base surface M, \(\varGamma \) is the surface singular curve along the junction with variable s along the length and \(\text {d}a\) is the differential surface element. Here the resultant surface forces \({{\varvec{f}}}_{1}\) are given on \(M_{1}\), the surface stress resultant \({{\varvec{n}}}_{1\nu }\) are given on boundary \(\partial M_{1}\setminus \partial M_{f}\), and the resultant boundary forces \({{\varvec{n}}}_{1}^{*}\) acting along the boundary \(\partial M_{f}\) can be represented by formulas (for more details see [18])

$$\begin{aligned}{} & {} {{\varvec{f}}}_{1}= \int _{-h_{1}^{-}}^{+h_{1}^{+}}{{\textbf {f}}}_{1}\mu _{1}\text {d}\xi _{1} +\alpha _{1}^{+}{{\textbf {t}}}_{1}^{*+}-\alpha _{1}^{-}{{\textbf {t}}}_{1}^{*-},\\{} & {} {{\varvec{n}}}_{1\nu }= \int _{-h_{1}^{-}}^{+h_{1}^{+}} \alpha _{1}^{*}{{\textbf {t}}}_{1n}\text {d}\xi _{1}, \quad {{\varvec{n}}}_{1}^{*}= \int _{-h_{1}^{-}}^{+h_{1}^{+}} \alpha _{1}^{*}{{\textbf {t}}}_{1}^{*}\text {d}\xi _{1}, \end{aligned}$$

where \(\mu \), \(\alpha ^{\pm }\) are geometric factors needed for the description of the differential volume element \(\text {d}v\) of B and the differential surface element \(\text {d}a\) of M.

In the procedure of integration through the shell thickness and bringing the 3D relations only to the base surface, we expand surface \(M_{1}\) up to the singular curve \(\varGamma \). As a result of such an extension of element \(B_{1}\) into the junction region, some fictitious surface forces are implicitly applied to this region. To get a correct form of the total force vector \({{\varvec{F}}}_{1}\) acting on the shell element \(B_{1}\), we have to integrate these additional forces and write them along the singular curve \(\varGamma \) and then subtract this term

here \(B_{1d}\) is the junction region where volume forces \({{\textbf {f}}}_{1}(\text {x})\) are applied and \(M_{1d}^{+}\), \(M_{1d}^{-}\) are surface stripes where surface forces \({{\textbf {t}}}_{1}^{*+}\), \({{\textbf {t}}}_{1}^{*-}\) are prescribed, respectively.

The total torque vector of spatial forces acting in \(B_{1}\) and on boundary \(\partial B_{1}\) defined on the base surface can be calculated using a through-the-thickness integration procedure, then

(5)

where the resultant surface couples \({{\varvec{c}}}_{1}\), the resultant stress couples \({{\varvec{m}}}_{1\nu }\), and the resultant boundary couples \({{\varvec{m}}}_{1}^{*}\) acting on \(\partial M_{1f}\) are given in the form (for more details see [18])

$$\begin{aligned}{} & {} {{\varvec{c}}}_{1}= \int _{-h_{1}^{-}}^{+h_{1}^{+}}\varvec{\zeta }_{1}\times {{\textbf {f}}}_{1}\mu _{1}\text {d}\xi _{1} +\alpha _{1}^{+}\varvec{\zeta }_{1}^{+}\times {{\textbf {t}}}_{1}^{*+} -\alpha _{1}^{-}\varvec{\zeta }_{1}^{-}\times {{\textbf {t}}}_{1}^{*-},\\{} & {} {{\varvec{m}}}_{1\nu }= \int _{-h_{1}^{-}}^{+h_{1}^{+}} \alpha _{1}^{*}\varvec{\zeta }_{1}\times {{\textbf {t}}}_{1n}\text {d}\xi _{1}, \quad {{\varvec{m}}}_{1}^{*}= \int _{-h_{1}^{-}}^{+h_{1}^{+}} \alpha _{1}^{*}\varvec{\zeta }_{1}\times {{\textbf {t}}}_{1}^{*}\text {d}\xi _{1}. \end{aligned}$$

Again, some additional fields related to the junction region have to be collected along the curve \(\varGamma \) and subtracted from the total torque vector \({{\varvec{T}}}_{o1}(M_{1})\) of all spatial forces acting in extended shell element \(B_{1}\) and on \(\partial B_{1}\)

The exact relations for the 3D position vector in the deformed placement are given by

$$\begin{aligned} {{\textbf {y}}}={{\varvec{y}}}+\varvec{\zeta }, \quad {{\textbf {y}}}^{+}={{\varvec{y}}}+\varvec{\zeta }^{+}, \quad {{\textbf {y}}}^{-}={{\varvec{y}}}+\varvec{\zeta }^{-}, \end{aligned}$$
(6)

and in the reinforcement region, the compensating couples should be reduced relative to the deformed singular curve \(\chi (\varGamma )\)

$$\begin{aligned} {{\textbf {y}}}={{\varvec{y}}}_{\varGamma }+\varvec{\zeta }_{\varGamma }, \quad {{\textbf {y}}}^{+}={{\varvec{y}}}_{\varGamma } +\varvec{\zeta }_{\varGamma }^{+}, \quad {{\textbf {y}}}^{-}={{\varvec{y}}}_{\varGamma } +\varvec{\zeta }_{\varGamma }^{-}. \end{aligned}$$
(7)

The same procedure should be used in the case of the description of the second shell element \(B_{2}\).

3 Reinforcement along shell junction

3.1 General beam theory

In the general theory, we consider a beam as a three-dimensional solid body in which one dimension, called length, is significantly greater than the others two, cross-sectional dimensions. In the undeformed (reference) placement it is identified with a region P. The beam boundary \(\partial P\) consists of three parts: initial \(\varPi ^{-}\) and final \(\varPi ^{+}\) cross section of the beam and edge surface \(\partial P^{*}\), \(\partial P=\varPi ^{+}\cup \varPi ^{-}\cup \partial P^{*}\), see Fig. 4.

Fig. 4
figure 4

Reference and deformed configuration of the beam-like body

Full size image

The position vector \({{\textbf {x}}}\) of any point x in the undeformed configuration P can be given by

$$\begin{aligned} {{\textbf {x}}}{(}\varvec{\xi },s{)}={{\varvec{x}}}_{\varGamma }(s)+\varvec{\xi }_{\varGamma }{(}\xi ^{\alpha },s{)}, \end{aligned}$$
(8)

where \({{\varvec{x}}}_{\varGamma }(s)\) defines the position of the beam axis \(\varGamma \), s is still a variable along the arc length of the curve \(\varGamma \), and \(\xi ^{\alpha }\), \(\alpha =1,2\) describes the position of a point in the cross section \(\varPi (s)\), relative to the axis \(\varGamma \).

The position vector \({{\textbf {y}}}\) of any point y in the deformed (current) configuration can be expressed formally as

$$\begin{aligned} {{\textbf {y}}}{(}\varvec{\xi },s{)}={{\varvec{y}}}_{\varGamma }(s)+\varvec{\zeta }_{\varGamma }{(}\xi ^{\alpha },s{)}, \end{aligned}$$
(9)

where the three-dimensional vector function \(\varvec{\zeta }_{\varGamma }{(}\xi ^{\alpha },s{)}\) defines a position of the point \(\text {y}(\xi ^{\alpha },s)\) relative to an actual beam axis \({{\varvec{y}}}_{\varGamma }(s)={{\textbf {y}}}(0,0,s)\).

In the referential description, the 3D global equilibrium equations of a regular beam can be expressed by vanishing the total force and torque vectors of all spatial forces acting on beam-like body P with the boundary \(\partial P\)

(10)

where \({{\textbf {f}}}\) is the volume force field acting on P and \({{\textbf {t}}}^{*}\) is the surface force vector acting on boundary surface \(\partial P\).

The exact one-dimensional equilibrium equations on the beam axis \(\varGamma \) are derived by direct integration of the 3D global equilibrium conditions of continuum mechanics over the beam cross section, see Fig. 5. The total force and torque vectors of spatial forces acting in P and boundary \(\partial P\) defined on the curve \(\varGamma \) are given by

$$\begin{aligned}{} & {} {{\textbf {F}}}(\varGamma )= \int _{\varGamma }\left( {{\varvec{n}}}'_{P}+ {{\varvec{f}}}_{P} \right) \text {d}s ={{\textbf {0}}},\nonumber \\{} & {} {{\textbf {T}}}_{\text {o}}(\varGamma )= \int _{\varGamma }\left\{ {{\varvec{m}}}'_{P}+ {{\varvec{y}}}_{\varGamma }'\times {{\varvec{n}}}_{P} +{{\varvec{c}}}_{P} +{{\varvec{y}}}_{\varGamma }\times \left( {{\varvec{n}}}'_{P} +{{\varvec{f}}}_{P}\right) \right\} \text {d}s={{\textbf {0}}}, \end{aligned}$$
(11)

where \({{\varvec{f}}}_{P}\) and \({{\varvec{c}}}_{P}\) are one-dimensional resultant forces and torque vectors statically equivalent to the real 3D body forces \({{\textbf {f}}}\) and surface forces \({{\textbf {t}}}^{*}\) acting on the P and \(\partial P^{*}\), and the following definitions are introduced

and the definition of the integral \(\int _{a}^{b}G'\text {d}x=G(x)\mid _{a}^{b}\) has been applied.

Fig. 5
figure 5

Reduction of the 3D beam-like body to the 1D resultant model

Full size image

3.2 Equilibrium conditions of the irregular shell with reinforcement

Using the surface Cauchy theorem, there exists the surface stress resultant tensor \({{\varvec{N}}}(x)\) and the surface stress couple tensor \({{\varvec{M}}}(x)\) (the first Piola–Kirchhoff type) such that

$$\begin{aligned} {{\varvec{n}}}_{\nu }={{\varvec{N}}}\varvec{\nu },\quad {{\varvec{m}}}_{\nu }={{\varvec{M}}}\varvec{\nu }, \end{aligned}$$

where \(\varvec{\nu }\) is the unit vector externally normal to boundary \(\partial M\). Here the generalized divergence theorem at the piecewise smooth surface M can be applied, Div is the surface divergence operator on M, ax(.) means the axial vector of the skew tensor (.), and \({{\varvec{F}}}=\nabla {{\varvec{y}}}\) is the shell deformation gradient where \(\nabla \) is the surface gradient operator on M.

Now global two-dimensional equilibrium conditions of irregular shell reinforced by beam along junction can be expressed by vanishing of the 2D total force and torque vectors, see Fig. 6

where

$$\begin{aligned} {{\varvec{f}}}_{\varGamma }={{\varvec{f}}}_{P} -{{\varvec{f}}}_{1 \varGamma }-{{\varvec{f}}}_{2 \varGamma }, \quad {{\varvec{c}}}_{\varGamma }={{\varvec{c}}}_{P} -{{\varvec{c}}}_{1 \varGamma }-{{\varvec{c}}}_{2 \varGamma }, \end{aligned}$$

and the above relations are the exact static equivalents of the 3D global equilibrium conditions of a shell-like body with a beam along the junction.

The nonlinear local shell equilibrium conditions have to be satisfied: local static equilibrium equations at each regular point of \(M\setminus \varGamma \)

$$\begin{aligned}{} & {} Div{{\varvec{N}}}+{{\varvec{f}}}={{\textbf {0}}},\nonumber \\{} & {} Div{{\varvec{M}}}+ax{(}{{\varvec{NF}}}^{T}-{{\varvec{FN}}}^{T}{)}+{{\varvec{c}}}={{\textbf {0}}}, \end{aligned}$$
(12)

local static boundary conditions at each regular point of \(\partial M_{f}\)

$$\begin{aligned} {{\varvec{n}}}^{*}-{{\varvec{N}}}\varvec{\nu }={{\textbf {0}}},\quad {{\varvec{m}}}^{*}-{{\varvec{M}}}\varvec{\nu }={{\textbf {0}}}, \end{aligned}$$
(13)

and static continuity conditions at each regular point of \(\varGamma \)

$$\begin{aligned}{} & {} {{\varvec{n}}}'_{P} +{{\varvec{f}}}_{\varGamma } -[\![{{\varvec{N}}}\varvec{\nu }]\!]={{\textbf {0}}},\nonumber \\{} & {} {{\varvec{m}}}'_{P}+ {{\varvec{y}}}'_{\varGamma }\times {{\varvec{n}}}_{P} +{{\varvec{c}}}_{\varGamma } -[\![{{\varvec{M}}}\varvec{\nu }]\!]={{\textbf {0}}}, \end{aligned}$$
(14)

where

$$\begin{aligned}{}[\![{{\varvec{N}}}\varvec{\nu }]\!]= \sum _{k=1}^{2}{{\varvec{N}}}_{k}\varvec{\nu }_{k}, \quad [\![{{\varvec{M}}}\varvec{\nu }]\!]= \sum _{k=1}^{2}{{\varvec{M}}}_{k}\varvec{\nu }_{k}. \end{aligned}$$

Here double square brackets denote the jump of discontinuous fields, while the prime is the derivative with respect to the arc length s along a singular curve \(\varGamma \).

Fig. 6
figure 6

Deformation of an irregular shell: reference (on the left) and actual (on the right) configurations

Full size image

4 Kinematic relations

Within the general nonlinear resultant shell and beam theory, we discuss the static problem of two-folded shells with reinforced junctions. In the deformed placement:

  • the shell is represented by the position vector \({{\varvec{y}}}\) of the deformed material base surface \(\chi {(}M{)}\) and the rotation tensor \({{\varvec{Q}}}\in SO\text {(3)}\)

    $$\begin{aligned} {{\varvec{y}}}={{\varvec{x}}}+{{\varvec{u}}},\quad {{\varvec{d}}}_{\alpha }={{\varvec{Q}}}{{\varvec{x}}}_{,\alpha }={{\varvec{Q}}}{{\varvec{a}}}_{\alpha },\quad {{\varvec{d}}}={{\varvec{Q}}}\varvec{\eta }, \end{aligned}$$
    (15)

    where three directors \(({{\varvec{d}}}_{\alpha },{{\varvec{d}}})\) are defined at each point of the regular base surface, \({{\varvec{u}}}\in E\) is the translation vector of M, \({{\varvec{Q}}}\) is the proper orthogonal tensor \({{\varvec{Q}}}^{T}={{\varvec{Q}}}^{-1}\), \(\text {det}{{\varvec{Q}}}=+1\);

  • the beam is represented by the position vector \({{\varvec{y}}}_{\varGamma }\) of the deformed material surface curve \(\chi {(}\varGamma {)}\) and the rotation tensor \({{\varvec{Q}}}_{\varGamma }\)

    $$\begin{aligned} {{\varvec{y}}}_{\varGamma }={{\varvec{x}}}_{\varGamma }+{{\varvec{u}}}_{\varGamma },\quad {{\varvec{d}}}_{i \varGamma }={{\varvec{Q}}}_{\varGamma }{{\varvec{A}}}_{i}, \end{aligned}$$
    (16)

    where three directors \({{\varvec{d}}}_{i \varGamma }\) are defined at each point of the surface curve, \({{\varvec{A}}}_{i}\), \(i=1,2,3\) are orthogonal vectors in the reference configuration, and \({{\varvec{u}}}_{\varGamma }\) is the translation vector of \(\varGamma \).

The kinematics of the shell is described by independent translation \({{\varvec{u}}}\) and rotation \({{\varvec{Q}}}\) fields and coincides with the kinematics of the 2D Cosserat continuum. For the description of the beam representing the reinforcement along the junction, we apply the Cosserat curve model which is kinematically consistent with the general shell theory.

In the general theory of shells, the strain and bending tensors \({{\varvec{E}}}\) and \({{\varvec{K}}}\) in the spatial representation are defined by the formulas

$$\begin{aligned}{} & {} {{\varvec{E}}}=\varvec{\varepsilon }_{\alpha }\otimes {{\varvec{a}}}^{\alpha },\quad {{\varvec{K}}}=\varvec{\kappa }_{\alpha }\otimes {{\varvec{a}}}^{\alpha },\nonumber \\{} & {} \varvec{\varepsilon }_{\alpha }={{\varvec{y}}}_{,\alpha }-{{\varvec{d}}}_{\alpha },\quad \varvec{\kappa }_{\alpha }=\frac{1}{2}{{\varvec{d}}}^{i}\times {{\varvec{Q}}}_{,\alpha }{{\varvec{Q}}}^{T}{{\varvec{d}}}_{i}, \end{aligned}$$
(17)

where \({(}{{\varvec{a}}}^{\alpha },\varvec{\eta }{)}\) and \({(}{{\varvec{d}}}^{i}{)}\) are the base reciprocal to \({(}{{\varvec{x}}}_{,\alpha },\varvec{\eta }{)}\) and \({(}{{\varvec{d}}}_{\alpha },{{\varvec{d}}}{)}\), respectively, \(\varvec{\varepsilon }_{\alpha }\) and \(\varvec{\kappa }_{\alpha }\) are strain measures vectors, \(\otimes \) is the tensor product of vector space.

In the general theory of beams, the vector measures of strains, energetically coupled with vectors of cross-sectional forces and moments, in the spatial representation are defined by

$$\begin{aligned} \varvec{\varepsilon }_{\varGamma }={{\varvec{y}}}'_{\varGamma }-{{\varvec{Q}}}_{\varGamma }{{\varvec{A}}}= {{\varvec{y}}}'_{\varGamma }-{{\varvec{d}}}_{\varGamma }, \quad \varvec{\kappa }_{\varGamma }=ax\left( {{\varvec{Q}}}'_{\varGamma }{{\varvec{Q}}}^{T}_{\varGamma }\right) , \end{aligned}$$
(18)

where \(\varvec{\varepsilon }_{\varGamma }\) and \(\varvec{\kappa }_{\varGamma }\) are stretching and bending vectors, respectively, and \(ax(\dots )\) denotes the axial vector of skew-symmetric tensor \((\dots )\).

In this case, we assume that the shell junction along \(\varGamma \) is stiff, which means that the deformation is continuous on the whole \(M=M_{1}\cup M_{2}\) including \(\varGamma \). Then both fields \({{\varvec{y}}}\) and \({{\varvec{Q}}}\) satisfy the dependencies

$$\begin{aligned}{} & {} {{\varvec{y}}}_{1}={{\varvec{y}}}_{2}={{\varvec{y}}}_{\varGamma },\quad [\![{{\varvec{y}}}]\!]=0,\quad [\![{{\varvec{y}}}']\!]=0,\\{} & {} {{\varvec{Q}}}_{1}={{\varvec{Q}}}_{2}={{\varvec{Q}}}_{\varGamma },\quad [\![{{\varvec{Q}}}]\!]=0,\quad [\![{{\varvec{Q}}}']\!]=0. \end{aligned}$$

We have to note that the Cosserat curve model is kinematically consistent with the six-parameter shell theory. In particular, one can describe the stretching, bending, and torsion of reinforcement together with the deformations of the shell.

5 Conclusions and discussion

Within the general nonlinear resultant shell theory called also the six-parameter shell theory, we discuss the static problem of two-folded shells with reinforced junctions. In more complex geometries of the junctions, we can apply the same procedure but the reduction process should be slightly modified. Two or more regular shell elements of the irregular structure have to be extended into the junction region, and then the surplus of additional resultant forces and couples must be subtracted along \(\varGamma \).

The obtained equilibrium conditions (12)–(14) describe the connection of two regular shell elements reinforced with a beam along the junction and are written on the reference base surface consisting of two regular surfaces joined together along the common singular curve. Presented conditions are the result of through-the-thickness integration of shell elements and over the cross section of beam elements of 3D global equilibrium conditions of continuum mechanics. The continuity conditions obtained along the singular curve \(\varGamma \) modelling the junction with the reinforcement take into account the correction of surface and volume fields resulting from the double integration of certain areas. Here, the singular surface curve is assumed to model the axis of the beam and, at the same time, the common edge of basic surfaces of shell elements. New, resultant local continuity conditions along the reinforced junction are valid for arbitrary shell thickness, internal through-the-thickness structure, and different material properties of the shell and beam elements. Using the six-parameter shell theory, we take into account the drilling moment that can play an important role in the modelling of multi-folded shells.

The kinematics of the shell coincides with the kinematics of the 2D Cosserat continuum that is described by independent translation and rotation fields. For modelling the reinforced junctions, the Cosserat curve was used, which is kinematically consistent with the general shell theory. The obtained 2D exact, resultant equilibrium conditions together with kinematic relations and constitutive equations formulate the complete boundary value problem for the irregular shell with reinforcement by beam along the junction.

The presented here technique could be also useful for description of kinematics of more complex shell-type structures, such as lattice-type shells [7, 16, 39, 42], where the exact description of kinematics of jointed beams could be essential, and other lattice-type or granular materials, see, for example, [9, 13] and the references therein.

Note that here we restrict ourselves to statics and material reinforcements. The presented above results can be easily transformed into a quasistatic case. Similar techniques based on the through-the-thickness integration could be also applied to non-material interfaces such as phase interface studies for elastic [12] and viscoelastic [11] shells. So various material properties are admissible. In this case, a non-material reinforcement plays the role of line tension with complex rheology as studied in [32] for statics. In fact, such a non-material interface may also model fracture or edge (wrinkle) formation. As fracture or similar phenomena could be essentially three-dimensional, whereas the shell theory is two-dimensional by definition, some additional assumptions could be necessary in this case, see, for example, the analysis of the correspondence between 2D and 3D Eshelby tensors performed in [10].

The static conditions can be also extended to dynamics. This case requires more essential modification including linear and rotatory inertia as was discussed in [21] for regular shells. Considering a shell as a 2D Cosserat continuum, these conditions can be treated as so-called transmission conditions, see, for example, [24, 26, 27, 31, 37, 38] for Cosserat continua and couple-stress theory. Let us note that since the Cosserat model with constrained rotations is a rather particular case, it requires a modification of kinematical compatibility conditions, and, as a result, the discussed interface conditions may differ from the general Cosserat continuum. This matter can be studied by considering related 2D shell models with constrained rotations.

Finally, let us mention that the discussed compatibility conditions can be also treated within the surface elasticity approach based on the Steigmann-Ogden model [43], see also [14, 17] for a discussion of interface and transmission conditions considering surface stresses.