1 Introduction

According to statistics [7], more than 30% of the population in the world dies from diseases of the cardiovascular system. Among them, a significant part are diseases of the blood vessels (thrombosis, aneurysm, atherosclerosis), as well as their consequences, more specifically myocardial infarction, stroke, heart attack, etc. One of the most common causes of death in people in economically developed countries is atherosclerosis [26], associated with narrowing of the artery lumen due to the formation of atherosclerotic plaques near the walls of the vessel. For the diagnosis and treatment of cardiovascular diseases, it is often necessary to evaluate blood flow in the vessels. In order to study the nature of blood flow through the vessels, many studies have been conducted on this topic, describing the relationship between various hemodynamic parameters, such as viscosity, erythrocyte aggregation and hematocrit. Also, the scientific literature describes numerous approaches to modeling blood flow, based on various theories and various dependencies of the characteristics of the blood flow from each other. The solution of the problem of modeling blood flow through the vessels is extremely important for medicine, and, in particular, for surgery, and can be used for both in the diagnosis of diseases and, for example, in reconstructive operations on the vessels.

One of the most significant factors affecting the flow of blood through the vessel is its viscosity, the value of which depends on many parameters. Within the framework of this paper, two approaches to modeling blood flow will be considered, taking into account the dependence of blood viscosity on the aggregation of erythrocytes and their organization in the flow. The first one relates to consideration of changes in the microinertia tensor, which can play a role of a microstructural tensor with a kinetic equation of its own. The second approach is based on the introduction of a volume fraction of red blood cells. As an assessment of the effectiveness of the approaches, a comparison of the obtained results with experimental data will be given. In addition, the application of the obtained models to the description of the flow of blood through various vessels of the human body and through a vessel of variable radius will be demonstrated.

2 Aspects of modeling blood flow in a blood vessel

2.1 Some medical characteristics of blood flow

Blood is a suspension of particles of a characteristic shape in an intercellular substance called blood plasma circulating through the blood vessels. The particles are divided into three types: erythrocytes (red blood cells), platelets and leukocytes (white blood cells). The most numerous among them are erythrocytes, which take 99% of the general volume of blood cells, and as a result, most significantly affect the blood flow [6]. Blood plasma consists of water and proteins dissolved in it and other organic and inorganic substances. The viscosity of blood plasma, as well as the viscosity of a suspension of erythrocytes in physiological saline, is of constant value, essentially depending only on the composition and structure of the substances contained in the plasma, and practically only on the concentration of erythrocytes. The viscosity of blood, however, due to the hydrodynamic interaction of the shaped particles with plasma, is not constant and depends on many factors.

Experiments have been carried out to demonstrate the non-Newtonian flow behavior of blood. In [2], results of an experiment to determine blood viscosity depending on the shear rate and the so-called hematocrit (the volume fraction of blood cells) were reported. Three blood samples were studied at different hematocrit values obtained by dilution. Based on the results, it was concluded that the viscosity increases as the velocity gradient decreases and the content of blood cells increases. The dependence of blood viscosity on temperature is presented in [1]: As temperature increases, viscosity decreases monotonically. However, these experiments were carried out outside the human body, and the results may differ to some extent from the in vivo dependencies. At temperatures within which a person is viable, the viscosity does not change significantly, which simplifies modeling.

The rheological properties of blood, including the dependence of viscosity on shear rate and temperature, are largely determined by the ability of erythrocytes to form and destroy aggregates, to deform, and to redistribute in the blood flow [18]. Aggregation occurs due to the interaction of protein structures of blood plasma with erythrocytes. At low shear rates, erythrocytes can more easily combine with each other, creating more and more resistance to flow, as a result of which the viscosity increases [6]. As the velocity gradient increases, erythrocytes separate from each other and the viscosity, while decreasing, eventually becomes almost constant. An increase in hematocrit (the volume fraction of blood cells) enhances the formation of aggregates and thereby increases blood viscosity. The influence of temperature on the formation of aggregates is also obvious. With an increase in temperature, aggregates are destroyed due to thermal motion [1], which causes a decrease in viscosity. In addition, a sufficiently large velocity gradient near the walls of the vessel provokes the displacement of erythrocytes toward the axis of the vessel, resulting in the formation of larger aggregates in the center of the vessel, and a cell-free layer of plasma appears near its walls. Thus, the viscosity at the axis of the vessel is greater than at the periphery, which means that the viscosity (or aggregation) depends on the radial coordinate. The dimensions of the vessel are also of great importance, since the formation of aggregates is more pronounced in narrower vessels [23]. In arterioles, venules and capillaries, due to their radius, the effect of the redistribution of erythrocytes in the flow becomes more significant [19]. The greater the ability of erythrocytes to aggregate (which, among other things, may depend on the presence of pathologies in a person), the greater the thickness of the free layer near the walls of the vessel and the greater the value of the viscosity near the central axis [28]. However, there is an exception: In very thin capillaries, the diameter of which is comparable to the size of an erythrocyte, the viscosity, decreases due to the alignment of erythrocytes along the axis of the vessel and the lubricating effect of the plasma along the edges [6]. This phenomenon is called the Fåhreus–Lindqvist effect and will not be considered in this work.

It is also necessary to look at the effect of erythrocyte deformation on blood viscosity [28]. Changing the shape of deformed cells affects the resistance to flow, but it is not as significant as the other effects, so erythrocytes are often considered as rigid, which will also be assumed in this work. The presence of platelets and leukocytes in the blood will also not be taken into account, since they occupy a negligibly small part of the volume and have almost no effect on the blood flow, except in cases of pathologies in which the concentration of these cells greatly increases. The effect of plasma viscosity on blood viscosity can be significant, since plasma properties largely determine the ability of erythrocytes to aggregate; however, in this work, plasma viscosity will be considered constant, since its change, as a rule, occurs only due to pathologies.

In view of the variable nature of blood viscosity, the radial velocity profile of its flow is flatter than in the case of Poiseuille flow, where the viscosity is constant [25]. In thin vessels, in which the so-called Fåhreus–Lindqvist effect is observed, the velocity increases near the walls of the vessel due to the free layer of plasma, which makes the velocity profile even flatter. There are various experiments to determine the blood velocity profile. In this work, the obtained numerical results will be compared with the experimental data described in [14].

2.2 Basic approaches to blood flow modeling

There are many different approaches to modeling the flow of blood through the vessels. The simplest description is by representing blood as a Newtonian fluid with a constant effective viscosity. This approach gives satisfactory results only for vessels of large diameters, since they form fewer erythrocyte aggregates that affect the viscosity. In narrow vessels, the use of such a description significantly loses accuracy [17]. However, in the case of large vessels, the interaction of blood with the elastic vascular wall becomes significant. In narrow vessels, this interaction can be neglected, considering the vessel wall to be non-deformable, but the ability of erythrocytes to aggregate increases and significantly affects the viscosity [23]. Several methods have been proposed to define a variable viscosity. One of them is the introduction of the dependence of blood viscosity on shear rate. There are also models with a variable distribution of viscosity depending on the radial coordinate. For example, in [15] it was proposed to treat the viscosity near the axis of the vessel as constant, and starting from a certain coordinate denoting the appearance of a cell-free layer, decreasing toward the walls of the vessel. This approach is well applicable to the description of the flow in capillaries. However, it should be taken into account that the thickness of the free plasma layer depends on the radius of the vessel. In addition, a two-phase model is often used to model blood flow, in which erythrocytes are considered as solid (or deformable) elliptical particles in a homogeneous liquid plasma [15, 21].

In this work, a blood flow model will be proposed that, to some extent, combines the approaches described above. The dependence of viscosity on erythrocyte aggregation, which depends both on the velocity gradient and on the radial coordinate, will be taken as a basis. As a characteristic of aggregation, two parameters will be proposed—the moment of inertia averaged over space (following a concept of micropolar theory, [4]) and the volume fraction of erythrocytes. In the second case, it will be necessary to use a two-phase model to calculate the effective viscosity depending on the volume fraction. The blood flow is described by a combination of the Navier–Stokes and incompressibility equations [13]. Erythrocytes are considered as rigid bodies, the relationship of viscosity with temperature, plasma viscosity and the content of platelets and leukocytes in the blood is not taken into account, as well as the deformation of the vascular wall. In addition, the problem is treated as axially symmetric, since there is no reason for a dependence of the flow parameters on the angular coordinate.

2.3 Erythrocyte geometry

An erythrocyte has the shape of a spheroid, slightly flattened in the center [8]. Large diameters are approximately 8.5 \(\upmu \)m, the maximum thickness is on average 2.4 \(\upmu \)m, and the minimum thickness is 1 \(\upmu \)m. In two-phase erythrocyte-plasma models, the flattening of the spheroid is often neglected in order to simplify the simulation. Sometimes erythrocytes are even roughly considered spherical, but such an assumption significantly affects the accuracy of the result, which, among other things, will be demonstrated in this work. Furthermore, we will consider an erythrocyte as a spheroid without central flattening with radii of 4 \(\upmu \)m and 1.1 \(\upmu \)m. The geometry used in this work is shown in Fig. 1. Usually, for finding effective properties, the values of the radii are not as important as the oblateness characteristic \(\gamma \), expressed as the ratio of the minor to the major semiaxis,

$$\begin{aligned} \gamma =\frac{r}{R}. \end{aligned}$$
(2.1)

For an erythrocyte, this characteristic is 0.275. Also, in problems with a suspension of particles of different sizes, volume matters, however, within the framework of this work, erythrocytes are considered to be the same and their volume is sufficiently characterized by a volume fraction.

Another important geometric characteristic is the moment of inertia. Due to the axial symmetry of the erythrocyte, it has two independent components. So the erythrocyte inertia tensor is given by

$$\begin{aligned} \varvec{{J}}_e=J_1\varvec{n}\varvec{n}+J_2\left( \varvec{\mathrm I}-\varvec{n}\varvec{n}\right) , \end{aligned}$$
(2.2)

where \(\varvec{n}\) is the unit vector codirectional with the axis of symmetry, \(\varvec{\mathrm I}\) is the unit tensor of the second rank, and \(J_1\), \(J_2\) are given by the formulae

$$\begin{aligned} J_1=\frac{2}{5}R^2=6.4\;\upmu \text {m}^2,\;\;J_2=\frac{1}{5}{(R}^2+r^2)=3.442\;\upmu \text {m}^2. \end{aligned}$$
(2.3)
Fig. 1
figure 1

Simplified geometry of a human erythrocyte

Full size image

2.4 Important assumptions

The main objective of this paper is to describe the flow of blood through a vessel of constant or variable radial cross section. For a given vessel geometry and velocity at the channel inlet, it is required to obtain the values of pressure, the radial and longitudinal velocity components of the steady flow at each point of the considered section of the channel. Based on these data, it is possible to determine profiles of velocities and pressure in the selected cross section of the vessel, as well as graphs of the dependence of these quantities on the coordinate along the channel axis.

The flow of blood will be based on the Navier–Stokes-type equation:

$$\begin{aligned} \rho \frac{\partial \varvec{v}}{\partial t}\ +\rho \varvec{v}\cdot \nabla \varvec{v}=-{\nabla p}+{\nabla }\cdot \left[ {^4}\varvec{\mu }:({\nabla }\varvec{v})\right] , \end{aligned}$$
(2.4)

where \(\rho \) is the density of the fluid, \(\varvec{v}\) is the velocity, p is the pressure, \({^4}\varvec{\mu }\) is the rank four viscosity tensor, \(\cdot \) stands for the dot product, and \(\nabla \) is the nabla operator in cylindrical coordinates defined by

$$\begin{aligned} \nabla \ =\frac{\partial }{\partial r}\varvec{e_r}+\frac{1}{\rho }\frac{\partial }{\partial \varphi }\varvec{e_\varphi }+\frac{\partial }{\partial z}\varvec{e_z}. \end{aligned}$$
(2.5)

The cylindrical coordinate system is chosen here for convenience, since the vessels are cylindrical in shape. The axial symmetry mentioned above gives the problem a two-dimensional form, eliminating all components that depend on the \(\varphi \) coordinate. Therefore, the velocity takes the form

$$\begin{aligned} \varvec{v}(t,\ r,\ z)=v_r(t,r,\ z)\varvec{e}_r+v_z(t,\ r,\ z)\varvec{e}_z, \end{aligned}$$
(2.6)

where \(v_r\) and \(v_z\) are the radial and axial components, respectively. In addition, we will consider blood as an incompressible liquid with a constant density \(\rho =1050\;\text {kg/m}^3\). Then, adding the incompressibility equation, we obtain a system of the form

$$\begin{aligned} \rho \frac{\partial \varvec{v}}{\partial t}+\rho \varvec{v}\cdot {\nabla }\varvec{v}=-{\nabla p}+{\nabla }\cdot {^4}\varvec{\mu }:({\nabla }\varvec{v}),\;\;{\nabla }\cdot \varvec{v}=0. \end{aligned}$$
(2.7)

This system of equations is still incomplete, since the components of \({^4}\varvec{\mu }\) are not constant, but depends on the factors described above. The purpose of this work is to extend the definition of the system (2.7), taking into account the empirical dependencies of the viscosity components on the aggregation of erythrocytes and their redistribution in the blood flow, as well as to solve this system.

However, such an incomplete form of the system of equations already allows us to introduce boundary conditions. At the walls of a vessel with radius R, it suffices to establish the no-slip condition:

$$\begin{aligned} \left. \ \ \varvec{v}\right| _{r=R}=0. \end{aligned}$$
(2.8)

At the entrance to the vessel, we will prescribe a horizontal velocity \(u_0\):

$$\begin{aligned} \begin{matrix}\left. v_z\right| _{z=0}=\ u_0,\;\;\left. v_r\right| _{z=0}=\ 0\\ \end{matrix}. \end{aligned}$$
(2.9)

At the exit from the section of the channel with length l, we require the condition for the independence of velocities from the cross section to hold, indicating that the flow has been established:

$$\begin{aligned} \begin{matrix} \left. \frac{\partial v_z}{\partial z}\right| _{z=l}=0,\;\;\left. \frac{\partial v_r}{\partial z }\right| _{z=l}=0\\ \end{matrix}. \end{aligned}$$
(2.10)

As a first approximation, the flow of blood through the vessels in the human body can be considered as stationary. Therefore, the distribution of velocities and pressures will not depend on time. However, in this work a non-stationary problem is solved. This allows to set a relatively simple boundary condition in the form of a horizontal velocity at the channel inlet, because over time and as one moves away from the initial coordinate, the velocity profile ceases to depend on the inlet profile. So only the flow rate plays a role. The values of velocities and pressures will correspond to the task set only at that moment and for those coordinates at which the flow is established both in time and in the cross section. In any case, the non-stationary problem requires us to introduce an initial condition. Therefore, let us assume that at time zero all velocities are equal to zero (there is no initial fluid flow in the channel):

$$\begin{aligned} \left. \varvec{v}\right| _{t=0}=0. \end{aligned}$$
(2.11)

Thus, we have an incomplete system of differential Eq. (2.7) with initial and boundary conditions for the speed determined by Eqs. (2.8)–(2.11). The following sections will describe the introduction of equations that close the system, the numerical solution of the problem and the analysis of the results obtained.

3 Modeling within the framework of micropolar theory

3.1 Viscosity as a function of aggregation

As described above, the variable nature of blood viscosity is largely due to the ability of red blood cells to form aggregates, thereby increasing resistance to flow. At high shear rates, viscosity increases with increasing aggregation, and at low shear rates, it decreases, which is associated with the formation of a cell-free layer in narrow vessels. This chapter will propose two ways to characterize aggregation in terms of a measurable physical quantity. In the first case, the spherical microinertia tensor, which correlates with the size of the formed aggregates, will be taken as such a characteristic, and in the second case, the volume fraction of erythrocytes, which shows the number of erythrocytes in the aggregate. The usefulness of introducing such parameters will be explained in the following sections.

When representing blood as a suspension of erythrocytes in plasma, it is necessary to take into account the orientation of spheroidal particles in space. For simplicity, the distribution of orientations can be considered random; then, the blood will show isotropy and the viscosity will be the same in all directions. In this case, the viscosity tensor of the fourth rank will become isotropic and the system (2.7) simplifies to

$$\begin{aligned} \rho \frac{\partial \varvec{v}}{\partial t}+\rho \varvec{v}\cdot {\nabla }\varvec{v}=-{\nabla p}+\big ({\nabla \mu }\left( A\right) \big )\cdot \left( \mathrm {\nabla }\varvec{v}\right) +\mu (A)\mathrm \Delta \varvec{v},\;\;{\nabla }\cdot \varvec{v}=0, \end{aligned}$$
(3.1)

where the parameter A characterizes the aggregation. In what follows, we consider two models for A, i.e., an averaged microinertia J and a volume faction of red cells \(\phi \). Note that in general a fourth rank tensor has two independent parameters but here one of them vanishes due to the incompressibility condition. Then, writing the first equation in terms of components along the radius and along the axis of the vessel in a cylindrical coordinate system, we obtain for the radial component

$$\begin{aligned}{} & {} \rho \frac{\left. \partial v_r(r,\ z\right) }{\partial t}+\rho \left( v_r(r,z)\frac{ \left. \partial v_r(r,z\right) }{\partial r}+v_z(r,z)\frac{\left. \partial v_r(r,z\right) }{\partial z}\right) \nonumber \\{} & {} \quad = -\frac{\left. \partial p(r,z\right) }{\partial r}+\frac{\partial \mu \left( A\right) }{\partial r}\frac{\left. \partial v_r(r,z\right) }{\partial r}+\frac{\partial \mu \left( A\right) }{\partial z}\frac{\left. \partial v_r(r,z\right) }{\partial z}\nonumber \\{} & {} \quad + \mu (A)\left( \frac{\left. \partial ^2v_r(r,z\right) }{\partial r^2}+\frac{1}{r}\frac{\left. \partial v_r(r,z\right) }{\partial r}-\frac{\left. v_r(r, z\right) }{r^2}+\frac{\left. \partial ^2v_r(r,z\right) }{\partial z^2}\right) , \end{aligned}$$
(3.2)

and for the component along the z-axis

$$\begin{aligned}{} & {} \rho \frac{\left. \partial v_z(r,z\right) }{\partial t}+\rho \left( v_r\left( r,z\right) \frac{\left. \partial v_z(r,z\right) }{\partial r}+v_z\left( r,z\right) \frac{\left. \partial v_z(r,z\right) }{\partial z}\right) \nonumber \\{} & {} \quad = -\frac{\partial p\left( r,z\right) }{\partial z}+\frac{\partial \mu \left( A\right) }{\partial r}\frac{\partial v_z\left( r,z\right) }{\partial r}+\frac{\partial \mu \left( A\right) }{\partial z}\frac{ \partial v_z\left( r,z\right) }{\partial z}\nonumber \\{} & {} \quad + \mu (A)\left( \frac{\left. \partial ^2v_z(r, z\right) }{\partial r^2}+\frac{1}{r}\frac{\left. \partial v_z(r,z\right) }{\partial r}+\frac{\left. \partial ^2v_z(r,z\right) }{\partial z^2}\right) . \end{aligned}$$
(3.3)

However, in order to describe the flow of blood through narrow capillaries, the assumption of a random distribution of orientations becomes erroneous, since erythrocytes line up along the axis of the vessel. In this case, transversal isotropy is appropriate to be used, and the viscosity tensor of the fourth rank is represented in the T-tensor base as follows,

$$\begin{aligned} {^4}\varvec{\mu }=\sum _{p=1}^{6}\mu _p{^4}\varvec{T}_p, \end{aligned}$$
(3.4)

where the tensors \({^4}\varvec{T}_p\) have the form [11]

$$\begin{aligned} \begin{aligned} {^4}\varvec{T}_1&=\overline{\varvec{E}}\,\overline{\varvec{E}},\;\;{^4}\varvec{T}_2={^4}\varvec{\overline{I}}-\frac{1}{2 }\overline{\varvec{E}}\overline{\varvec{E}},\;\;{^4}\varvec{T}_3= \overline{\varvec{E}}\varvec{m}\varvec{m},\;\;{^4}\varvec{T}_4=\varvec{m} \varvec{m}\overline{\varvec{E}},\\ {^4}\varvec{T}_5&=\left( \varvec{m}\overline{\varvec{E}}\varvec{m}\right) ^s=\frac{1}{4}\left( \varvec{e}_k\varvec{m}\varvec{e}_k\varvec{m} +\varvec{m}\varvec{e}_k\varvec{m}\varvec{e}_k+\varvec{m}\varvec{e}_k\varvec{e}_k\varvec{m}+\varvec{e}_k\varvec{m}\varvec{m}\varvec{e}_k\right) ,\;\;{^4}\varvec{T}_6=\varvec{m}\varvec{m}\varvec{m}\varvec{m},\\ \overline{\varvec{E}}&=\varvec{\mathrm I}-\varvec{m}\varvec{m},\;\; {^4}\varvec{\overline{ I}}=\frac{1}{2}\left( \varvec{e}_k\varvec{e}_s\varvec{e}_k\varvec{e}_s+\varvec{e}_k\varvec{e}_s\varvec{e}_s\varvec{e}_k\right) ,\;\;\varvec{e}_k,\varvec{e}_s\bot \varvec{m},\;\; k,s=1,2. \end{aligned} \end{aligned}$$
(3.5)

Here, \(\varvec{m}\) is a unit vector of the transversally isotropy axis. Note that \(\varvec{m}\) rotates with the fluid flow in general, so one should introduce a kinetic equation for it. Within the framework of this paper, the problem is solved numerically only for the case of isotropy. The case of erythrocytes aligned along one axis and the intermediate case of predominant orientation of erythrocytes in one direction, which is characteristic of the transition of larger vessels to thin capillaries, are left to future work, for which foundations have been laid herewith.

3.2 Moment of inertia as a microstructural parameter in spatial description

In Eringen’s theory of micropolar media [5], the inertia tensor of a continuum element in combination with its angular velocity makes it possible to describe the rotation of particles of a material continuum as a solid body. In this case, the form and shape of the inertia tensor do not change on the scale of a continuous medium. However, for some materials this property is no longer valid. In [3, 9], an extension of the original micropolar theory was proposed within the framework of a spatial field description, in which the elementary volume contains different microparticles at different times, and which is most appropriate for fluid problems. In this formulation, structural changes become possible due to the consolidation or defragmentation of particles, as well as the outflow and inflow of matter in an elementary volume. The inertia tensor of an elementary volume becomes a new, independent microstructural parameter, capable of changing, for which an additional constitutive equation is required.

In context of the blood flow problem, it is convenient to use the moment of inertia as a characteristic of erythrocyte aggregation. It can change depending on the formation or destruction of aggregates, as well as due to the redistribution of cells in the blood stream. Within the framework of the approach described in [9], the inertia tensor as a property at the macrolevel is introduced by averaging over the elementary volume V. Let N erythrocytes and their aggregates with mass \(m_i\) and inertia tensor \(\varvec{\hat{J}_i}\). Then, the specific moment of inertia \(\varvec{J}\) of the elementary volume is equal to

$$\begin{aligned} \varvec{J}=\frac{1}{m}\sum _{i=1}^{N}\varvec{\hat{J}}_i,\;\; m= \frac{1}{N}\sum _{i=1}^{N}m_i. \end{aligned}$$
(3.6)

Single erythrocytes in the blood can be randomly oriented, while their aggregates usually have an irregular shape and completely different sizes. At the same time, the homogenized inertia tensor is spherical at the continuum level and is equal to

$$\begin{aligned} \varvec{J}=J\varvec{\mathrm I}. \end{aligned}$$
(3.7)

Isotropy appears due to the random distribution of aggregates in orientation, size and shape, and in the context of vessels, the diameter of which is comparable to the size of an erythrocyte loses its validity.

Within the framework of the spatial description, the moment of inertia can change not only due to the rotation of particles as solid bodies (which corresponds to the rotation of the inertia tensor together with the particle), but also due to the flow of inertia and internal structural transformations. Then, the balance equation of the moment of inertia is written in the following form

$$\begin{aligned} \frac{\mathrm d\varvec{J}}{\mathrm dt}=\varvec{\omega }\times \varvec{J}-\varvec{J}\times \varvec{\omega }+\varvec{\chi }, \end{aligned}$$
(3.8)

where \({\varvec{\chi }}\) is a source term that can be a function of various quantities, depending on the problem, and \(\varvec{\omega }\) is an angular velocity, see [9, 24]. Note that in the case (3.7) the dependence on \(\varvec{\omega }\) disappears. This gives us the possibility to not consider a balance of spin here. This introduces a new governing equation, a kinetic one. However, it seems reasonable to consider a approximate algebraic form for the moment of inertia. In other words, instead of an exact solution of the corresponding kinetic equation we propose to introduce its reasonable approximate solution directly. For example, within the framework of this work, the steady flow of blood with a viscosity that depends on aggregation, characterized by the moment of inertia, is of interest. Then, having a system of Eq. (3.1) with \(\mu =\mu (J)\), it suffices to introduce an algebraic expression for the moment of inertia in the form

$$\begin{aligned} J=\hat{J}\left( \frac{\partial v}{\partial r},\ r,\ z\right) . \end{aligned}$$
(3.9)

Here, aggregation parameter is introduced as a function of coordinates and shear rate. This form will be explained in detail below. As mentioned earlier, the dependence of aggregation on temperature, the properties of blood plasma, and the content of other cells in the blood, except for erythrocytes, will not be taken into account. For the considered flow, the angular velocity is zero. So the balance of spin is fulfilled trivially. As a result, we have a system of equations

$$\begin{aligned} \rho \frac{\partial \varvec{v}}{\partial t}+\rho \varvec{v}\cdot {\nabla }\varvec{v}=-{\nabla p}+\big ({\nabla \mu }\left( J\right) \big )\cdot \left( {\nabla }\varvec{v}\right) +\mu (J)\mathrm \Delta \varvec{v},\;\;{\nabla }\cdot \varvec{v}=0,\;\;J=\hat{J}\left( \frac{\partial v}{\partial r},r,z\right) . \end{aligned}$$
(3.10)

An empirical formula for the function \(\hat{J}\) will be presented below, based on the studied dependencies of aggregation on the flow parameters.

To begin with, let us consider how the ability of erythrocytes to aggregate depends on the velocity gradient at a fixed coordinate. It is known that at very low shear rates the viscosity decreases with increasing aggregation, while at high shear rates it increases. The dependence of viscosity on the shear rate is experimentally obtained in [2], Fig. 2.

Fig. 2
figure 2

Dependence of blood viscosity on shear rate after [2]

Full size image

Combining the above, we can approximately designate the nature of the dependence of aggregation on the shear rate. It turns out that with an increase in the shear rate, aggregations first grow, starting from a certain value, then begin to decrease and, in the limit, reach a minimum value equal to the moment of inertia of a single erythrocyte. The increase at low shear rates can be neglected since it only concerns very thin vessels. Then, for a fixed radius, an empirical expression for the moment of inertia can be written in the following form

$$\begin{aligned} \hat{J}\left( \frac{\partial v}{\partial r},r=\text {const.},z=\text {const.}\right) =\frac{M}{C+\frac{\partial v}{\partial r}}+J_{\textrm{min}}, \end{aligned}$$
(3.11)

where M, C are some constants, and \(J_{\textrm{min}}\) is the minimum moment of inertia.

Now, let us investigate how the aggregation will depend on the radial coordinate at a fixed shear rate. Erythrocytes tend to migrate to the axis of the vessel, as a result of which aggregation grows toward the center of the channel, since it is easier for cells to stick together with each other. Meanwhile, at the edges of the channel, near the walls, aggregates are not formed and the value of aggregation is minimal. Then, at a certain value of the velocity gradient, we will consider the distribution of aggregation over the cross section to be constant in the center of the vessel and decreasing linearly to zero near the walls of the vessel according to the formula

$$\begin{aligned} \hat{J}\left( \frac{\partial v}{\partial r}=\text {const.},r,z=\text {const.}\right) =\frac{K}{h}\left( 1-\frac{r}{R}\right) , \end{aligned}$$
(3.12)

where K is a constant, R is the radius of the vessel, and h is the thickness of the free plasma layer, i.e., a layer free from erythrocytes, near the walls of the vessel, expressed as a fraction of the radius. The value of h depends on the radius of the vessel and can be determined from experimental graphs [21]. Combining expressions (3.11) and (3.12), we obtain an empirical formula expressing the dependence of the moment of inertia on the velocity gradient and coordinates,

$$\begin{aligned} \begin{aligned}&\hat{J}\left( \frac{\partial v}{\partial r},r,z\right) =\frac{B}{C+\frac{\partial v}{\partial r}}+J_{\textrm{min}},\;\; \frac{r}{R}<1-h;\\&\hat{J}\left( \frac{\partial v}{\partial r},r,z\right) =\frac{1}{h}\left( \frac{B}{C+\frac{\partial v}{\partial r}}+J_{\textrm{min}}\right) \left( 1-\frac{r}{R(z)}\right) ,\;\;\frac{r}{R}\ge 1-h, \end{aligned} \end{aligned}$$
(3.13)

where B, C are some constants, \(J_{\textrm{min}}\) is the minimum moment of inertia, and R is the channel radius, generally variable, depending on the position of the cross section or, in other words, the z-coordinate. Thus, the following equation for the moment of inertia has been formulated, which complete the system of Eq. (3.10). The resulting system reads:

$$\begin{aligned} \begin{aligned} \rho \frac{\partial \varvec{v}}{\partial t}+\rho \varvec{v}\cdot {\nabla }\varvec{v}&=-{\nabla p}+\Big ({\nabla \mu }\big (\hat{J}\left( {\nabla v},r,z\right) \big )\Big )\cdot \left( {\nabla }\varvec{v}\right) +\mu \big (\hat{J}\left( {\nabla v},r,z\right) \big )\mathrm \Delta \varvec{v},\\ {\nabla }\cdot \varvec{v}&=0,\\ \hat{J}\left( \frac{\partial v}{\partial r},r,z\right)&=\frac{B}{C+\frac{\partial v}{\partial r}}+J_{\textrm{min}},\;\; \frac{r}{R}<1-h,\\ \hat{J}\left( \frac{\partial v}{\partial r},r,z\right)&=\frac{1}{h}\left( \frac{B}{C+\frac{\partial v}{\partial r}}+J_{\textrm{min}}\right) \left( 1-\frac{r}{R(z)}\right) ,\;\; \frac{r}{R}\ge 1-h. \end{aligned} \end{aligned}$$
(3.14)

Taking into account the correlation of the variable nature of viscosity with aggregation, we assume that the dependence of viscosity on the moment of inertia is linear,

$$\begin{aligned} \mu =C_1J+\mu _0, \end{aligned}$$
(3.15)

where \(\mu _0\) is the blood plasma viscosity. Thus, blood viscosity is the sum of plasma viscosity and the influence of red blood cells on viscosity. This formulation allows to set the plasma viscosity \(\mu _0\) as a parameter and, if necessary, change it. For the numerical solution, the value \({\mu _0=0.0014~\text {Pa}\cdot \text {s}}\) is used.

The next step is to determine all the constants present in the system in order to make it possible to solve it numerically. The minimum moment of inertia, as mentioned earlier, is numerically equal to the moment of inertia of a single erythrocyte in units of \(\text {m}^2\). However, the erythrocyte has the shape of a spheroid and its inertia tensor has two components. Since the constitutive Eq. (3.13) is valid for a homogenized isotropic inertia tensor (more precisely, its only component), then the value of \(J_\textrm{min}\) should be taken as the component of the erythrocyte inertia tensor averaged over space, written in the form (2.2). Then, denoting the average value by angular brackets, one should write

$$\begin{aligned} \langle \varvec{J}_e\rangle =J_1\langle \varvec{n}\varvec{n}\rangle +J_2\big (\varvec{\mathrm I}-\langle \varvec{n}\varvec{n}\rangle \big ). \end{aligned}$$
(3.16)

Considering that the resulting tensor must be isotropic, and calculating the trace of both tensors, we get \(\left\langle \varvec{n}\varvec{n}\right\rangle =\frac{1}{3}\varvec{\mathrm I }\), which leads to the equation

$$\begin{aligned} \langle \varvec{J}_e\rangle =\left( \frac{1}{3}J_1+\frac{2}{3}J_2\right) \varvec{\mathrm I}, \end{aligned}$$
(3.17)

where the expression in brackets is taken as \(J_{\textrm{min}}\).

The remaining coefficients present in the system (3.14) are found on the basis of the dependence of viscosity on the velocity gradient, measured experimentally in [2], taken at a radial coordinate equal to half the radius of the vessel. The obtained values of the constants of the system (3.14) and the relation (3.15) are equal to

$$\begin{aligned} \begin{aligned}&B =8\cdot 10^{-12}\;\tfrac{\text {m}^2}{\text {s}},\; C =1.2\,\text {s}^{-1},\;C_1 =4.5\cdot 10^8 \tfrac{\text {Pa}\cdot \mathrm s}{\text {m}^2},\\&\mu _0=0.0014\;\text {Pa}\cdot \text {s},\;J_{\textrm{min}}=4.428\cdot 10^{-12}\;\text {m}^2. \end{aligned} \end{aligned}$$
(3.18)

Thus, the task of blood flow through a vessel of variable diameter with a viscosity depending on the aggregation of erythrocytes, characterized by an isotropic moment of inertia, has been posed.

3.3 Effective viscosity

One of the most common problems in the theory of heterogeneous (or, in a broad sense, multicomponent) media is the search for so-called effective properties. Considering a certain volume of a heterogeneous medium, in which there is a number of inhomogeneities large enough so that it can be considered as representative, one can introduce, for example, average stresses and strains. The elastic constants connecting them will be called the effective properties of this volume. Finding the effective parameters is associated with the homogenization of the medium within a representative volume. Thus, the transition from the micro- to the macrolevel is carried out. Detailed studies on this topic can be found, for example, in [10] or in [11].

In the context of this work, it is interesting to find the effective blood viscosity, taking into account the contribution of individual erythrocytes to the resistance to plasma flow. The effective viscosity of the fluid flow connects the stress tensor \(\varvec{\tau }\) and the strain rate tensor \(\dot{\varvec{\varepsilon }}\) according to

$$\begin{aligned} \varvec{\tau }=2\,{^4}\varvec{\mu }:\dot{\varvec{\varepsilon }}, \quad \dot{\varvec{\varepsilon }}=\frac{1}{2}\left( \nabla \varvec{v}+\nabla \varvec{v}^\intercal \right) . \end{aligned}$$
(3.19)

In order to determine the effective properties in the theory of heterogeneous media, microstructural parameters are introduced, which represent the real contribution of individual inhomogeneities to the property under consideration, and which make it possible to give a quantitative characteristic of the microstructure [11]. Determining such parameters is, in general, a non-trivial task. Most often, the volume fraction \(\phi \) is used as a microstructural parameter, but it is not suitable for all problems.

In this work, erythrocytes will be considered as randomly oriented spheroids, identical in terms of shape and volume. This allows us to use the volume fraction of cells as a microstructural parameter on which the effective viscosity depends. Meanwhile, the task is complicated by the variable nature of this volume fraction. Indeed, the formation and destruction of aggregates can be described not only by a change in the moment of inertia, as was done in the previous section, but also by an increase and decrease in the concentration (or volume fraction) of erythrocytes depending on the coordinate and shear rate. In the approach that uses the moment of inertia, the aggregates are characterized by their size, while the volume fraction parameter assesses the number of erythrocytes in one aggregate. Thus, similarly to the reasoning above, we come to the conclusion that it is necessary to introduce a defining equation for the volume fraction of erythrocytes,

$$\begin{aligned} \phi =\hat{\phi }\left( \frac{\partial v}{\partial r},\ r,\ z\right) . \end{aligned}$$
(3.20)

Then, the system of equations describing the blood flow, using the approach described above, can be written as

$$\begin{aligned} \begin{aligned} \rho \frac{\partial \varvec{v}}{\partial t}+\rho \varvec{v}\cdot {\nabla }\varvec{v}&=-{\nabla p}+{\nabla }\cdot \left[ {^4}\varvec{\mu }_{\textrm{eff}}(\phi ):({\nabla }\varvec{v})\right] ,\\ {\nabla }\cdot \varvec{v}&=0,\\ \phi&=\hat{\phi }\left( \frac{\partial v}{\partial r},\ r,\ z\right) . \end{aligned} \end{aligned}$$
(3.21)

Since the volume fraction of erythrocytes characterizes their aggregation, its constitutive equation can be written in a form similar to (3.13). Indeed, it makes sense to introduce the dependence of this quantity on the velocity gradient and coordinates based on the same empirical dependencies as in the previous section. Then, the third equation in the system (3.21) takes the form

$$\begin{aligned} \begin{aligned}&\hat{\phi }\left( \frac{\partial v}{\partial r},r,z\right) =\frac{A_1}{A_2+\frac{\partial v}{\partial r}}+\phi _0,\;\; \frac{r}{R}<1-h,\\&\hat{\phi }\left( \frac{\partial v}{\partial r},r,z\right) =\frac{1}{h}\left( \frac{A_1}{A_2+\frac{\partial v}{\partial r}}+\phi _0\right) \left( 1-\frac{r}{R(z)}\right) ,\;\;\; \frac{r}{R}\ge 1-h. \end{aligned} \end{aligned}$$
(3.22)

where \(A_1\), \(A_2\) are constants, R is the radius of the vessel, depending on the z-coordinate in the case of a variable cross section, \(\phi _0\) is the minimum volume fraction of erythrocytes in the blood, and h is the thickness of the free plasma layer.

The question of determining the dependence of the effective viscosity \({^4}\varvec{\mu }_{\textrm{eff}}(\phi )\) on the volume fraction of erythrocytes remains open. In general, the contribution of individual inhomogeneities to the effective property is influenced by their interaction with each other. However, this interaction is often neglected and inhomogeneities are considered as isolated. This approach is called the non-interaction approximation (NIA). Its main task is the determination of the contribution of an individual inhomogeneity to a common property, taking into account the shape, orientation, and material constants inherent in this inhomogeneity [10, 11].

NIA introduces tensors for the characterization of various properties (for example, the stiffness contribution tensor [11]). These characterize the contribution of individual particles to an effective property. In [10], the tensor of the contribution of fluidity, that is, the value of the inverse viscosity, was introduced. Indeed, the doubled strain rate tensor in a representative volume containing an isolated particle (in this case, an erythrocyte) can be written as

$$\begin{aligned} 2\varvec{\varepsilon }={^4}\varvec{f_0}:\varvec{\tau _0}+2\mathrm \Delta \varvec{\varepsilon }, \end{aligned}$$
(3.23)

where \({^4}\varvec{f_0}\) is the fluidity tensor of the environment (in this case, blood plasma), \(\varvec{\tau _0}\) is the stress tensor in the considered volume, and \(\mathrm \Delta \varvec{\varepsilon }\) is additional velocity tensor due to the influence of the erythrocytes. Since \(\mathrm \Delta \varvec{\varepsilon }\) is a function of \(\varvec{\tau _0}\), one may write

$$\begin{aligned} 2\varvec{\varepsilon }={^4}\varvec{f_0}:\varvec{\tau }_0+\frac{V_*}{V}{^4}\varvec{L}:\varvec{\tau }_0=\underbrace{\left( {^4}\varvec{f}_0+\frac{V_*}{V}{^4}\varvec{L}\right) }_{{^4}\varvec{f_*}}:\varvec{\tau }_0, \end{aligned}$$
(3.24)

where \({^4}\varvec{L}\) is the rank four fluidity contribution tensor, the ratio \(\frac{V_*}{V}\) characterizes the erythrocyte volume fraction, and \({^4}\varvec{f_ *}\) denotes the effective fluidity tensor. The contribution tensor depends on the shape of the erythrocyte (that is, its oblateness \(\gamma \)) and on the viscosity of the blood plasma. In [10], it was proposed to draw an analogy between the case of viscosity and elasticity and put

$$\begin{aligned} {^4}\varvec{L}=2{{^4}\varvec{H}}_{{G_0}=\mu _0,\; K_0=\infty }^{\textrm{rigid}}, \end{aligned}$$
(3.25)

where \({^4}\varvec{H}\) is the compliance tensor of an absolutely solid particle of unit volume in an incompressible elastic matrix, obtained for a particle of the same shape by replacing the shear modulus \(G_0\) by the viscosity of the background fluid \(\mu _0\).

According to [11], for the elasticity problem, the tensor \({^4}\varvec{H}\) can be represented as

$$\begin{aligned} {^4}\varvec{H}=\frac{V_*}{V}\left[ \left( {^4}\varvec{S}_1-{^4}\varvec{S}_0\right) ^{-1}+{^4}\varvec{Q}\right] ^{-1}, \end{aligned}$$
(3.26)

where \({^4}\varvec{S}_0\), \({^4}\varvec{S}_1\) are the compliance tensors of the matrix and of the particle, and \({^4}\varvec{ Q}\) is the Hill tensor (see Chapter 4, [11]). Since the erythrocyte has the shape of a spheroid with axial symmetry, the tensors \({^4}\varvec{L}\), \({^4}\varvec{H}\), \({^4}\varvec{S}\), \({^4}\varvec{Q}\) can be expanded in the transversely isotropic basis (3.5) as follows:

$$\begin{aligned} \begin{aligned}&{^4}\varvec{H}=\sum _{p=1}^{6}h_p{^4}\varvec{T}_p,\;\;{^4}\varvec{L}=\sum _{p=1}^{6}l_p{^4}\varvec{T_p},\;\; l_p=2h_p,\\&{^4}\varvec{S}=\sum _{p=1}^{6}{s_p(G,\ K)}{^4}\varvec{T}_p,\;\;\; {^4}\varvec{Q}=\sum _{p=1}^{6}q_p(G,\gamma ){^4}\varvec{T}_p. \end{aligned} \end{aligned}$$
(3.27)

Here, G, K are the shear and the bulk modulus, respectively. Then, putting the tensors in the form (3.27) into (3.26) and passing to the tensor of the contribution of fluidity, setting \(\mu _1=K_1=\infty \) for an absolutely solid erythrocyte and \(K_0=\infty \) for an incompressible blood plasma, we obtain the components of the tensor \({^4} \varvec{L}\):

$$\begin{aligned} \begin{aligned}&l_1=-\frac{1}{36\mu _0f_1},\;\;l_2=-\frac{1}{\mu _0\left( f_0+f_1\right) },\;\;l_3=l_4=\frac{1}{18\mu _0f_1},\\&l_5=-\frac{2}{\mu _0\left( {1-f}_0-4f_1\right) },\;\;l_6=-\frac{1}{9\mu _0f_1}, \end{aligned} \end{aligned}$$
(3.28)

where the functions \(f_0\), \(f_1\) are functions of the erythrocyte oblateness \(\gamma \) according to the formulas (2.1):

$$\begin{aligned} \begin{aligned}&f_0=\frac{\gamma ^2(1-g)}{2(\gamma ^2-1)},\;\;f_1=\frac{\gamma ^2}{4\left( \gamma ^2-1\right) ^2}\Big (\left( 2\gamma ^2+1\right) g-3\Big ),\\&g\left( \gamma \right) =\frac{1}{\gamma \sqrt{1-\gamma ^2}}\arctan \frac{\sqrt{1-\gamma ^2}}{\gamma },\;\;\gamma <1. \end{aligned} \end{aligned}$$
(3.29)

Taking into account the random orientation of erythrocytes in the blood flow, we average the tensor of the contribution of fluidity over space,

$$\begin{aligned} \left\langle {^4}\varvec{L}\right\rangle =\frac{6l_1+2l_2+l_5}{5}\left( {^4}\varvec{\mathrm I}-\frac{1}{3}\varvec{\mathrm I}\varvec{\mathrm I}\right) . \end{aligned}$$
(3.30)

Taking into account that all coefficients in the expansion of the contribution tensor in the transversally isotropic basis are a number divided by the plasma viscosity, we obtain for the effective isotropic tensor

$$\begin{aligned} {^4}\varvec{f_*}=f_0\left( {^4}\varvec{\mathrm I}-\frac{1}{3}\varvec{\mathrm I}\varvec{\mathrm I}\right) +\frac{1}{\mu _0}\phi M\left( {^4}\varvec{\mathrm I}-\frac{1}{3}\varvec{\mathrm I}\varvec{\mathrm I}\right) , \end{aligned}$$
(3.31)

where \({^4}\varvec{\mathrm I}\) is the unit tensor of the fourth rank and \(M=\mu _0\frac{6l_1+2l_2+l_5}{5}\). Then, for each component of the yield tensor we obtain

$$\begin{aligned} f=f_0+\frac{1}{\mu _0}M\phi . \end{aligned}$$
(3.32)

And, therefore, for viscosity as a reciprocal:

$$\begin{aligned} \mu =\frac{\mu _0}{1+M\phi }. \end{aligned}$$
(3.33)

The formula (3.33) was also obtained in [10]. The value of the numerical parameter M depends only on the shape of the spheroid, or rather, on its oblateness \(\gamma \). Sometimes erythrocytes are roughly considered as balls, which simplifies the calculations, but at the same time leads to a rather strong decrease in the accuracy of the result. As part of this work, a comparison of such approaches with each other will be carried out. Table 1 shows the numerical values for the functions \(f_0\), \(f_1\) and the number M for inclusions in the form of spheres and spheroids with the value \(\gamma \) as in the geometry adopted above.

Table 1 Values of numerical constants for different forms of inclusions
Full size table

Thus, the problem of blood flow through a vessel of variable diameter with a viscosity depending on the variable volume fraction of erythrocytes is described by the following system of equations

$$\begin{aligned} \begin{aligned} \rho \frac{\partial \varvec{v}}{\partial t}+\rho \varvec{v}\cdot {\nabla }\varvec{v}&=-{\nabla p}+\left( {\nabla }\left( \frac{\mu _0}{1+M\phi \left( \frac{\partial v}{\partial r},r,z\right) }\right) \right) \cdot \left( {\nabla }\varvec{v}\right) +\frac{\mu _0}{1+M\phi \left( \frac{\partial v}{\partial r},r,z\right) }\mathrm \Delta \varvec{v},\\ \mathrm {\nabla }\cdot \varvec{v}&=0,\\ \hat{\phi }\left( \frac{\partial v}{\partial r},r,z\right)&=\frac{A_1}{A_2+\frac{\partial v}{\partial r}}+\phi _0,\;\;\frac{r}{R}<1-h,\\ \hat{\phi }\left( \frac{\partial v}{\partial r},r,z\right)&=\frac{1}{h}\left( \frac{A_1}{A_2+\frac{\partial v}{\partial r}}+\phi _0\right) \left( 1-\frac{r}{R(z)}\right) ,\;\;\frac{r}{R}\ge 1-h. \end{aligned} \end{aligned}$$
(3.34)

The constants \(A_1\), \(A_2\) and \(\phi _0\) are taken such that the dependence of the viscosity on the velocity gradient at a radial coordinate equal to half the radius of the vessel corresponds to the experimental curve obtained in [2]. Thus, the coefficients listed above are taken equal to

$$\begin{aligned} A_1=0.74 \mathrm s^{-1},\;\;A_2=6.34 \mathrm s^{-1},\;\;\phi _0=0.19. \end{aligned}$$
(3.35)

The value of \(\phi _0\) correlates well with its physical meaning—the minimum value of the volume fraction of erythrocytes (or hematocrit) in the human body.

It should be noted that in this formulation the problem of blood flow can be generally solved for nonrandom orientations of erythrocytes. Thus, the area of applicability of its solution has been significantly increased. For example, in narrow capillaries, erythrocytes tend to line up along the axis of the vessel so that their axis of symmetry is perpendicular to the flow. With the transition of larger vessels into narrow ones, erythrocytes, depending on the radius of the cross section, are characterized by one or another preferential orientation. In such situations, the viscosity tensor of the fourth rank will be transversally isotropic, which, when substituted into (2.4), will give a two-dimensional viscosity with components, one of which is responsible for the flow resistance along the radius, and the second resists the movement along the vessel axis. Within the framework of this paper, such an extension was not implemented, but this opens up new possibilities for modeling blood flow. Also, to describe blood flow in narrow capillaries, other constitutive equations for the moment of inertia and the volume fraction of erythrocytes can be written.

4 Some remarks on the applied numerical technique

4.1 Justification of the finite volume method

In the previous sections, we have obtained systems of partial differential equations in the form (3.14) or (3.34). There are several methods for solving such equations numerically. The main methods for solving them together with certain boundary and initial conditions are the finite difference method, the finite volume method and the finite element method. In this work, the finite volume method was chosen. It seems necessary to give reasons for this choice in context with the description of blood flow.

First of all, it is necessary to explain why the finite element method was not used. The finite element method is the most common among all numerical methods for solving boundary value problems, since it is applicable to modeling a wide range of processes. This is due to its versatility, since it allows dividing essentially every domain into elements, even if it is very complex in shape. Also, this method is good in that it makes it possible to do a mesh refinement in the required subdomains, thereby increasing the accuracy of calculations [22]. However, in this work there is no complex geometry, because the vessel is a cylinder, even though it is of variable cross section. In this case, due to its complexity, the finite element method is inferior to the finite difference method.

The finite volume method, which is based on the division of the computational domain into control volumes carrying a value of the investigated field quantity in them, allows solving differential equations in an integral formulation. For each control volume, ratios are written that take the flow of quantities contained in the equation through the surface of this volume into account. The approximation of integral relations makes it possible to compose difference schemes for the numerical solution of the problem [12]. Thus, the finite volume method can be considered an extension of the finite difference method, which allows calculations for any shape of the control volume [27]. Again, the choice of this numerical method is motivated by the cylindrical shape of the computational domain of the problem, for which it is necessary to use a curvilinear grid.

In addition, the problem of blood flow is two-dimensional, which requires the use of an algorithm with splitting equations in two spatial directions—the radial and the longitudinal coordinate [12]. Otherwise, the difference scheme may turn out to be too complicated to solve, and the computational complexity will increase significantly.

4.2 Solution of the equations in dimensionless form

The use of numerical methods will always lead to numerical errors. In the present case, the calculated values will differ by several orders of magnitude. For example, the pressure can be of the order of \({10}^5\) Pa, and the velocity will be around \({10}^{-1}\) m/s. This issue is easily overcome by reducing the equations to a dimensionless form. To begin with, we note that for both of our formulations it is necessary to solve the set of the Navier–Stokes equation and the incompressibility equation with variable viscosity. The nature of the change in viscosity in the two formulations will be different, but will not affect the numerical scheme. Thus, the problem is reduced to solving the first two equations of (3.14) or (3.34) with the viscosity as a parameter given by some function outside the difference schemes for these equations. Dimensional and dimensionless variables involved in the equations are related by the following relations

$$\begin{aligned} \varvec{v}=\left[ V\right] \varvec{v}^\prime ,\;\;p=\left[ P\right] p^\prime ,\;\;t=\left[ T\right] t^\prime ,\;\;\nabla =\frac{1}{[L]}\nabla '. \end{aligned}$$
(4.1)

where square brackets denote dimensional coefficients, and new dimensionless variables are marked with a prime.

Substituting (4.1) into the first two equations of (3.14), we obtain

$$\begin{aligned} \rho \frac{[V]\partial \varvec{v}'}{[T]\partial t'}+\frac{\rho [V][V]}{[L]}\varvec{v}'\cdot \nabla '\varvec{v}'=-\frac{\left[ P\right] }{\left[ L\right] }\nabla 'p'+\frac{\mu \left[ V\right] }{\left[ L\right] \left[ L\right] }\mathrm \Delta '\varvec{v}',\;\;\frac{[V]}{[L]}\nabla '\cdot \varvec{v}'=0, \end{aligned}$$
(4.2)

or

$$\begin{aligned} \frac{\partial \varvec{v}'}{[T]\partial t'}+\frac{[V]}{[L]}\varvec{v}'\cdot \nabla '\varvec{v}'=-\frac{\left[ P\right] }{\rho \left[ L\right] [V]}\nabla 'p'+\frac{\mu }{\rho \left[ L\right] \left[ V\right] }\mathrm \Delta '\varvec{v}',\;\;\nabla '\cdot \varvec{v}'=0. \end{aligned}$$
(4.3)

Let us take the following relations for dimensional coefficients into account,

$$\begin{aligned} \left[ T\right] =\frac{\left[ L\right] }{\left[ V\right] },\;\;\left[ P\right] =\ \rho \left[ V\right] \left[ V\right] . \end{aligned}$$
(4.4)

For convenience, all dimensional coefficients should be combined into one parameter, on which the solution of the system will depend. Thus, the values of physical quantities will be effectively taken into account by means of this parameter. For the system in question, this parameter corresponds to the Reynolds number,

$$\begin{aligned} Re=\frac{\rho [L][V]}{\mu }. \end{aligned}$$
(4.5)

Then, in dimensionless form, the system of equations takes the form

$$\begin{aligned} \frac{\partial \varvec{v}^\prime }{\partial t^\prime }+\varvec{v}^\prime \cdot \nabla '\varvec{v}^\prime =-{\nabla }^\prime p^\prime +\frac{1}{Re}\mathrm \Delta '\varvec{v}',\;\;{\nabla }^\prime \cdot \varvec{v}^\prime =0. \end{aligned}$$
(4.6)

It is the introduction of the Reynolds number that makes it possible to take into account the variable nature of viscosity separately from the solution of the Navier–Stokes and incompressibility equations. In the case of a constant viscosity, the Reynolds number will be common for the entire computational domain, and for the case of non-Newtonian behavior, it can be calculated separately in each elementary grid cell. In this paper, the Reynolds number is a local characteristic that depends on the coordinates and velocity gradient in accordance with the choice of problem statement (3.14) or (3.34).

Of course, an adequate analysis of the results is possible with quantities that are not devoid of dimensions; therefore, at the end of the calculations, it is required, using transformations inverse to (4.1), to return back to dimensional quantities.

Further information regarding the finite volume element analysis when applied to system of dimensionless partial differential equations can be found in [16, 20].

5 Analysis and discussion of the obtained results

5.1 Comparison with experimental data

Many experimental studies have been carried out to determine the characteristics of blood flow through vessels of various radii. However, such studies cannot be carried out with sufficient accuracy in a vessel with a variable cross section. Thus, the mathematical model of blood flow can expand our knowledge for assessing blood flow in the human body. Nevertheless, in order to evaluate the effectiveness of the proposed model, first of all, it is necessary to compare the obtained results with the existing experimental data.

In the previous section of this work, an numerical procedure was chosen that can be used to solve the systems of equations in (3.14) or (3.34) for a given vessel geometry, velocity at the channel inlet and numerical coefficients that determine the nature of the dependence of viscosity on various flow parameters. It is necessary to compare the obtained velocity and pressure components with the experiment under the same input conditions. [14] presents results of measuring the velocity profile of blood flow through a narrow capillary with a radius of 27 \(\upmu \)m. At the same time, the average hematocrit was 33.5%, which is slightly lower than that of most people. Also, within the framework of the experiment, the axial pressure gradient was determined, which was 3736 dynes/cm\(^3\) (or 37,360 Pa/m in SI). Since in the formulation of the problem we have a given velocity at the channel inlet, and not a pressure gradient, as in the experiment, we will select the value of the input velocity at which a pressure drop corresponding to the experiment occurs in a vessel with a radius of 27 \(\upmu \)m in order to compare the results. The hematocrit value affects the choice of coefficients in (3.18) and (3.35), because they are selected for taking into account the experimental dependence of viscosity on the velocity gradient (see Fig. 2, [2]), which differs to some extent for different values of the average hematocrit. The values in (3.18) and (3.35) correspond to a hematocrit of 30%, which is close to the experimental parameters in [14]. The thickness of the free layer h for a vessel of this size is about 0.2 of the radius, which can be seen from the experimental data of [21].

Figure 3 shows graphs of the dependence of the horizontal component of the blood flow velocity on the radial coordinate, or, in other words, velocity profiles. The solid blue line represents the velocity profile obtained by applying the viscosity versus aggregation approach expressed by the moment of inertia. The orange line corresponds to the velocity profile calculated in the framework of the approach with effective viscosity depending on the volume fraction of erythrocytes. The black dotted line coincides with the experimental data obtained in [21].

Fig. 3
figure 3

Velocity profiles for two different modeling approaches in comparison with the experiment [21]

Full size image

From Fig. 3, we conclude that both approaches to modeling the blood flow describe well the reality of the experiment. At the same time, the model, taking into account the moment of inertia, gives the best convergence near the walls of the vessel, describing well the shape of the velocity profile, while the approach through the effective viscosity gives the best results near the channel axis, but describes the blood flow along its walls not so well. In order to quantify the discrepancy with the experiment, it is also possible to construct graphs of the error depending on the radial coordinate (Fig. 4). Here, the colors of the graphs corresponding to one or another approach coincide with the colors selected in the graphs of Fig. 4.

From the graphs, it can be seen that the discrepancy with the experimental data in the case of setting the dependence of the effective viscosity on the volume fraction of erythrocytes does not exceed 3% near the channel axis, but gives a significant discrepancy near the walls. In the framework of the approach with setting aggregation as the moment of inertia, the discrepancy with the experiment near the center of the channel is slightly higher, but does not exceed 5%, but near the walls of the vessel the discrepancy becomes much smaller than in the approach with effective viscosity. Taking into account the completely empirical nature of the constitutive equations for the microstructural parameters (3.13) and (3.22), this result can be considered good. However, it should be indicated that the discrepancies, which are noticeable for the most part at the walls of the channel, can be associated with the experiment. The differences may be due to the following factors.

Fig. 4
figure 4

Difference of the velocity profile from the experimental data from [21] for two approaches depending on the radial coordinate

Full size image

First, within the framework of the model, erythrocytes are considered randomly oriented. It can be seen from the graphs in Fig. 3 that, even in fairly narrow vessels, this assumption leads to good results. But, as the radius of the vessel decreases, the discrepancy will increase, since the erythrocytes will tend to direct their axis of symmetry perpendicular to the flow. Thus, blood cannot be considered as isotropic, since transversal isotropy will appear with a difference in properties in the direction of the radial coordinate. In this case, in the formulation with the moment of inertia, one will have to introduce two constitutive equations for two unequal components of the inertia tensor, and the effective viscosity will also be calculated for the case of transversal isotropy with two viscosity components.

Second, the Fåhreus–Lindqvist effect [6] was not fully taken into account in the problem. This fact is directly related to the already mentioned difference in the flow that occurs for very narrow capillaries. After all, the effect of reducing viscosity in vessels with a radius comparable to the size of an erythrocyte is explained precisely by the alignment of blood cells in a row along the flow, which contributes to the formation of a cell-free plasma layer along the walls of the vessel, due to which the viscosity decreases. The assumptions taken into account when compiling the empirical formula for the moment of inertia or the volume fraction of erythrocytes take into account the formation of a free layer along the walls of the vessel; however, the deformation and orientation of erythrocytes along the channel axis can make their own adjustments to the thickness of the free layer.

Third, the selection of coefficients (3.18) and (3.35), carried out on the basis of the approximation of the experimental dependencies [2] by an arctan function, is not without error. In addition, the dependence of viscosity on the velocity gradient for shear rates less than unity and a hematocrit of 33.5% remains unknown. Similarly, the minimum value of the moment of inertia of an erythrocyte is calculated from the assumption of its spheroidal shape, which is also a simplification. Thus, the correction of the coefficients of the constitutive equations can significantly affect the accuracy of the solution.

Fourth, this work does not take into account a number of factors that have a small but noticeable effect on blood flow. These are factors such as temperature, deformation of erythrocytes, blood levels of platelets, leukocytes, and other elements, changes in the properties of blood plasma [6, 19]. The last two factors are very individual in nature; therefore, their consideration is important only for modeling the blood flow in people with certain features of the blood composition, and in other cases their values can be considered average.

Thus, in summary, this model describes the real blood flow through thin vessels quite well, but the error in the velocity values near the walls of the vessel is much larger than that near the axis of the channel. In this case, the approach with the calculation of effective viscosity gives worse results at the boundaries than the model with consideration of the moment of inertia. Modeling the blood flow near the walls of the vessel during the formation of a free plasma layer is much more complicated than calculating the velocities near the center of the channel. Thus, there is an assumption that for large vessels, in which the thickness of the cell-free layer becomes negligibly small, the error of the solution is significantly reduced.

5.2 Influence of the shape of the erythrocyte

If the problem statement is used to model the blood flow using the dependence of the effective viscosity on the volume fraction of erythrocytes (3.34), the shape of the erythrocyte used in the model becomes a significant factor influencing the flow. Calculations using (3.25)–(3.33) are made on the assumption that the erythrocyte has the shape of a spheroid with the geometry described in a previous section of this work. At the same time, with the value of the spheroid oblateness parameter \(\gamma \)=0.275, the value of the numerical parameter M included in Eq. (3.33) is approximately equal to \(-3\). However, it should be shown how important it is to take into account the shape of an erythrocyte for describing the blood flow by the system of Eq. (3.34).

To simplify the model, erythrocytes are sometimes represented as spheres. This assumption, first, ensures isotropy, and second, it significantly speeds up calculations. For a spherical shape, the oblateness \(\gamma =1\), and the numerical parameter \(M=-2.5\). The advantages and disadvantages of such a formula are discussed, for example, in [10]. Within this work, the solution of the system of Eq. (3.34) was constructed taking into account the spheroidal shape of the erythrocyte, and without it. The results obtained in both cases were compared with experimental data [14]. All other model parameters, such as axial pressure gradient and free layer thickness, were taken similarly to the previous section. Figure 5 shows the obtained velocity profiles for spherical and spheroidal erythrocytes. The black dotted line indicates the experimental data [14].

Fig. 5
figure 5

Velocity profiles taking into account the shape of the erythrocyte

Full size image

From the graphs, it can be seen that taking into account the shape of an erythrocyte is practically not important when modeling the flow along the vessel walls. However, the velocity profile for other radial coordinates differs significantly for different forms of an erythrocyte. This is largely due to the fact that a free plasma layer is modeled at the boundaries of the vessel, in which the content of erythrocytes is almost zero, which makes the shape of the cells a useless parameter. At the same time, the shape of the erythrocyte plays a significant role near the center of the vessel. Simplification of the model in the form of taking red blood cells for balls gives a close value of the numerical parameter M to that calculated for spheroids; however, the velocity profile with such a simplification is significantly extended.

Thus, when modeling the blood flow, the form of the erythrocyte becomes an important factor. The difference in solutions is visible even for the case of isotropy, while the transversal isotropy arising due to a change in the orientation of erythrocytes in very narrow vessels becomes an insurmountable circumstance for models that simplify the shape of an erythrocyte to a sphere.

5.3 Flow in a vessel with a variable cross section

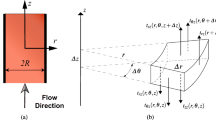
The human circulatory system has a complex structure, within which the radius of blood vessels changes when larger vessels pass into smaller ones and vice versa. In addition, with such pathologies as aneurysm, atherosclerosis, thrombosis, and others associated with a decrease in the lumen of the vessel, the radius also becomes a variable. In vessels of variable radius, it is much more difficult to evaluate the blood flow experimentally, so it is important that the blood flow model also works in the case of a variable cross section. Within the framework of this work, a solution to the system (3.14) was constructed by taking into account the dependence of blood viscosity on the aggregation variable in the case of partial occlusion of the vessel (Fig. 6, left). The initial vessel radius is 27 \(\upmu \)m, and the minimum lumen is approximately 20% of the initial diameter. At such radii, the thickness of the free layer is quite large and reaches 0.3 of the channel radius. The velocity at the entrance to the channel was taken the same as previously when compared with the experiment [14].

Consider a section of a vessel of variable radius with a narrowing geometry described for simplicity by a sinusoid (Fig. 6).

Fig. 6
figure 6

Converging vessel geometry and diagram of horizontal velocities

Full size image

As part of a more detailed study of blood flow in the case of vasoconstriction, we construct velocity profiles in various sections (Fig. 7). It can be seen that in the places of constriction the velocity profile is extended depending on the clearance. In this case, in the intermediate section, the velocity profile is deformed at the edges. This is due to the appearance of a radial velocity component due to the flow of blood from the walls to the center as it narrows. At the narrowest point, the velocity profile again has a characteristic form, since the radial velocities disappear again. An increase in the maximum horizontal velocity module as the vessel narrows is in good agreement with the jet continuity condition, under which the product of the vessel velocity and its area remains the same. This explains the strong increase in the velocity profile at the point of maximum narrowing.

Fig. 7
figure 7

Velocity profile in different sections of a converging vessel

Full size image

It is also interesting to look at the change in velocities and pressure along the axis of the channel. Graphs of the dependence of horizontal and radial velocity, as well as pressure, on the cross section of a narrowing vessel, characterized by the longitudinal coordinate z, are shown in Fig. 8.

Fig. 8
figure 8

Horizontal speed (top left), radial speed (top right) and pressure (bottom) as a function of the cross section of a converging vessel

Full size image

It can be seen that the horizontal velocity increases with decreasing diameter and decreases with the expansion of the vessel, returning to its original value. The radial velocity fluctuates around zero in the straight part of the channel and then appears as the radius of the vessel lumen decreases. (Blood flows from the walls to the center.) At the site of maximum narrowing, the radial velocity reaches zero and begins to grow in the opposite direction as the vessel expands. (Blood flows from the center to the walls.) The pressure in the straight part of the canal falls evenly and slowly compared to the strong pressure drop at the narrowing of the vessel lumen. Thus, the systems of Eqs. (3.14) or (3.34) work well for the case of contraction and expansion of the vessel.

5.4 Velocity profile in different vessels

The model of blood flow obtained in this work can be used to describe the flow of blood through various vessels of the human body. For example, one can build a profile of the speed of blood flow through the inferior vena cava. According to [6], the diameter of the inferior vena cava is about 2–3 cm, and the velocity takes a maximum value of about 0.25 m/s. In the calculations, the value of the radius was taken as 1.35 cm, and the thickness of the free layer in such large vessels is insignificant and is taken as 0.01 of the vessel radius. The resulting velocity profile is shown in Fig. 9.

Fig. 9
figure 9

Profile of the velocity of blood flow through the inferior vena cava

Full size image

It can be seen that the velocity profile does not differ much from the parabola at the edges of the vessel (in contrast to the capillary in [14]). This is due to the very small thickness of the cell-free layer formed in the inferior vena cava.

In the case of the carotid artery, the average diameter of which is 1 cm, and the maximum velocity reaches 0.2 m/s [6, 8], and the velocity profile also differs little from a parabola (Fig. 10). The thickness of the free layer in the carotid artery, as well as in the case of the inferior vena cava, is too small to have any noticeable effect on the velocities from the walls of the vessel.

Due to the absence of a pronounced cell-free layer in the described vessels of the human circulatory system, the accuracy of calculations should increase. However, it is worth taking into account the fact that the walls of large vessels are more elastic. Thus, due to the presence of pulse waves traveling through the vessels from the heart during the ejection of blood from it [6], the diameters of the inferior vena cava and carotid artery can vary significantly. Such fluctuations are not taken into account within the framework of the task and can introduce a significant error in the presented results.

Thus, within the framework of this work, a model was presented that makes it possible to evaluate the blood flow in various vessels of the human circulatory system, knowing their diameter and blood velocity (or axial pressure gradient).

Fig. 10
figure 10

Profile of blood flow velocity in the carotid artery

Full size image

6 Conclusions

In this paper, we pointed out that the behavior of blood flow through the vessels is essentially affected by the variable nature of blood viscosity, which depends on many parameters that change in a complex way in the bloodstream. The importance of evaluating and predicting the processes occurring in various vessels of the human body leads to the need for mathematical modeling of blood flow. As part of this work, the characteristic features of blood flow through the vessels depending on various hemodynamic parameters were studied and a blood flow model was developed that takes into account a dependence of viscosity on particle aggregation. Two approaches have been proposed to study the aggregation of erythrocytes—in the form of the moment of inertia of cells and their aggregates and in the form of a volume fraction of erythrocytes as a characteristic of the size of the aggregate.

As part of this work, the existing scientific literature related to the topic was examined. Medically oriented articles contain empirical information about the dependencies and interrelation of blood flow parameters. In contrast to that the engineering literature is based on a stringent mathematical description to describe the blood flow, which also defines its limitation. In the course of this work, the processes that determine the flow of blood through the vessels were studied and systematized. Factors that have the greatest influence on the viscosity were identified—the aggregation of erythrocytes and their organization in the blood flow, depending on the diameter of the vessel. Thus, fundamental parameters of hemodynamics were obtained that must definitely be taken into account in future models of blood flow. In addition, existing approaches to modeling the blood flow were studied, based on certain dependencies of viscosity that occur in the body.

Moreover, a mathematical model was developed that allows obtaining the speed and pressure in vessels of different diameters based on the property of erythrocytes to create aggregates and migrate to the axis of the vessel. The system of Navier–Stokes and incompressibility equations was supplemented by a third governing equation for a new microstructural parameter characterizing aggregation. Two modeling approaches have been proposed, one of which takes into account the moment of inertia as a characteristic of aggregation, and another one that takes the volume fraction of erythrocytes into account. The blood was presented as a suspension of plasma with randomly oriented spheroidal erythrocytes. The composed systems of equations were solved numerically. To this end, the finite volume method was chosen, which has a number of advantages over other methods. The resulting finite volume algorithm was implemented, taking into account both of the presented problem statements.

In order to demonstrate the effectiveness of the developed model, the obtained solution was compared with experimental data [14] presented for a narrow capillary. On that basis, it was shown that the proposed model describes the real blood flow through rather thin vessels quite well. However, for radial coordinates close to the outer radius, the model shows less accurate results than when approaching the vessel axis. This is largely due to the neglect of the influence on the blood flow of such factors as erythrocyte deformation and temperature. Also, the problem was solved only for the case of isotropy, which limits the possibilities of such a model in describing the blood flow through extremely narrow vessels comparable in diameter to the size of an erythrocyte. The two proposed approaches to the description of erythrocyte aggregation were compared with each other, which made it possible to draw conclusions about their applicability. In addition, within the framework of this work, the importance of taking into account the spheroidal shape of an erythrocyte was shown: The problem was solved for spherical and spheroidal particles, and a comparison of the solutions showed a sharp increase in the error when representing erythrocytes in the form of balls.

As an example of application of the proposed model, a flow in a pipe with a variable cross section was studied. It was shown how the velocity components and pressure change depending on the lumen of the narrowing pipe, and the velocity profiles obtained in different sections were compared with each other. Thus, the scope of applicability of the developed model was significantly expanded. Also, as part of the work, the possibility of describing the flow of blood through various vessels of the human circulatory system, in particular, through the carotid artery and inferior vena cava, was demonstrated.