Hamiltonian phase error in resonantly driven CNOT gate above the fault-tolerant threshold

Abstract

Because of their long coherence time and compatibility with industrial foundry processes, electron spin qubits are a promising platform for scalable quantum processors. A full-fledged quantum computer will need quantum error correction, which requires high-fidelity quantum gates. Analyzing and mitigating gate errors are useful to improve gate fidelity. Here, we demonstrate a simple yet reliable calibration procedure for a high-fidelity controlled-rotation gate in an exchange-always-on Silicon quantum processor, allowing operation above the fault-tolerance threshold of quantum error correction. We find that the fidelity of our uncalibrated controlled-rotation gate is limited by coherent errors in the form of controlled phases and present a method to measure and correct these phase errors. We then verify the improvement in our gate fidelities by randomized benchmark and gate-set tomography protocols. Finally, we use our phase correction protocol to implement a virtual, high-fidelity, controlled-phase gate.

Introduction

Spin qubits in solid-state devices¹ are a promising platform for large-scale quantum computers. Universal control has recently been demonstrated in a six-qubit device in Silicon², and a four-qubit device in Germanium³, marking a first step of scaling up spin qubit devices. Spin qubits in Silicon exhibit long coherence times^4,5, fast manipulation⁶ and ability to operate at an elevated temperature^7,8,9. The compatibility with the already matured semiconductor industry processes allows potential mass fabrication of such devices¹⁰, integration with cryo-electronics¹¹, and opens the potential for high-performance integrated quantum circuits in the future¹². Phase-flip code, a critical feature of large-scale quantum computers, has also been demonstrated recently^13,14. These progress make spin qubits a viable qubit platform for the future.

To implement large-scale quantum computers, the ability to implement quantum error correction code is required. One of the most promising quantum error correction codes is the surface code¹⁵. Typically, under certain assumptions of the error model, the surface code gives an error threshold of 1%¹⁶. High-fidelity single-qubit^4,17 and two-qubit gates^{18,19,20,21,22} which satisfy this error threshold, have been demonstrated with spin qubits in isotopically enriched Silicon. Among these results, the two-qubit gates are implemented as a controlled-phase (CZ) gate or controlled-rotation (CROT) gate. In contrast to the CROT gate, the CZ gate can be implemented with base-band gate pulses, eliminating the requirement for high-frequency signals typically in the range of GHz. However, a high-fidelity CZ gate requires fast and precise pulses to control the exchange coupling between two qubits because of the exponential dependence of the exchange coupling on the gate voltage¹⁹. The CROT gate, on the other hand, can be implemented in a less demanding way by keeping the exchange always on^18,23. In the exchange-always-on system, the CROT gate fidelity is reduced by a coherent off-resonant Hamiltonian phase error, which has the form of a controlled phase. This phase error must be mitigated to obtain high-fidelity CROT gates above the fault-tolerant threshold. Previous work avoids this problem by shifting the control microwave frequency¹⁸. The microwave frequency is adjusted by a feedback loop to minimize this phase error. Here, we systematically compensate for the effect of these phase errors by shifting the phase of the applied microwave pulses. We measure the phase errors with a calibration sequence and compensate the effects. Our procedure to compensate for these controlled-phase errors enables us to implement a CZ gate virtually, similar to a virtual single-qubit z-gate²⁴, thus without additional execution time in the quantum circuit. The ability to implement both high-fidelity CROT and a virtual CZ gate without complicated pulse engineering makes the exchange-always-on system interesting to study. Compared to a synthesized implementation using CZ gates^19,20, the CROT gate allows for a native, resonant CNOT logical gate with fidelity above the fault-tolerant threshold¹⁸, which makes this gate relevant for future spin-based quantum processors.

Here, we demonstrate a procedure to obtain a high-fidelity resonantly driven CROT gate in an exchange-always-on two-qubit system. We present a systematic way to measure the accumulated phase error and then a method to compensate for these gate errors. We use randomized benchmarking (RB) protocol^25,26 to compare the gate fidelity with and without compensation. We then perform gate-set tomography (GST)²⁷ to obtain the details on the error processes of our quantum gates using experimental and simulated data. The experimental and simulation data results show good agreement, which proves the validity of the quantum gate model we use for simulation. Finally, we demonstrate the implementation of a virtual high-fidelity CZ gate using the compensation method and benchmark the performance of this virtual CZ gate with GST.

Results

Device and controlled-rotation gates

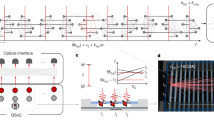
Figure 1a shows the device used for the experiment, which is a triple quantum dot device fabricated in an isotopically purified silicon quantum well, the same device as used in ef. ¹⁸. A three-layer aluminium gate stack is deposited to fabricate the gate electrodes, which control the electric confinement potential of the quantum dots. We apply an external magnetic field of B_ext = 0.408 T. A cobalt micro-magnet is deposited on the gate stack to induce a gradient magnetic field. The gradient magnetic field generated by the micro-magnet enables the individual adrresing of the spins in the quantum dots and the manipulation of the spin qubit state by performing electric dipole spin resonance (EDSR). The device has a charge sensor quantum dot in the upper part of the device and an array of three quantum dots in the lower part. We perform charge sensing with reflectometry²⁸ and accumulate an electron in the center (qubit Q₁) and right dot (qubit Q₂), while the leftmost dot is used as an extension of the left reservoir. Figure 1b shows the stability diagram around this configuration. Energy-selective single-shot readout is used for qubit readout and initialization²⁹.

Fig. 1: Two-qubit system.

a False-color scanning electron microscope image of a device identical to the one measured (scale bar 100 nm). The two quantum dots are formed below plunger gate electrodes P1 (Q₁) and P2 (Q₂), and the yellow circle indicates the charge sensor quantum dot. Quantum gates are implemented via electric dipole spin resonance in the gradient field of a micro-magnet (not shown) by applying microwave signals to the MW gate electrodes. b Charge stability diagram around the qubit operation condition. The number of electrons in two quantum dots is denoted as (N₁, N₂). Readout and initialization of qubit Q₁ (Q₂) are performed at square A (B). Qubit operations are executed at the charge symmetry point (circle C) to achieve high-fidelity two-qubit gates. c Energy level diagram of the two-qubit system. Exciting one of the four frequencies rotates the target qubit conditioned on the state of the other qubit, which allows the implementation of controlled-rotation (CROT) and zero-controlled-rotation (ZCROT) gates. The label X indicates a π/2 pulse around the x axis of the qubit Bloch sphere. d Electric dipole spin resonance peaks. The measured spectra show the transition frequencies of Q₁ when Q₂ is in $\left\vert \downarrow \right\rangle$ (blue) and $\left\vert \uparrow \right\rangle$ (purple) and the frequencies of Q₂ when Q₁ is in $\left\vert \downarrow \right\rangle$ (red) and $\left\vert \uparrow \right\rangle$ (orange).

As the exchange coupling between the two qubits is turned on, when the Zeeman energy difference δE_z between two qubits is much larger than the exchange coupling J, the energy levels of $\left\vert \uparrow \downarrow \right\rangle$ and $\left\vert \downarrow \uparrow \right\rangle$ are lowered, and the basis states that diagonalize the Hamiltonian become $\left\vert \uparrow \uparrow \right\rangle$, $\widetilde{\left\vert \uparrow \downarrow \right\rangle }\,$$\widetilde{\left\vert \downarrow \uparrow \right\rangle }$ and $\left\vert \downarrow \downarrow \right\rangle$. The two-qubit Hamiltonian diagonalized by these states is^23,30

$$H(t)\approx \frac{h}{2}\left(\begin{array}{cccc}2\bar{{E}_{{{{\rm{z}}}}}}&B(t)&B(t)&0\\ {B}^{* }(t)&\delta \tilde{{E}_{{{{\rm{z}}}}}}-J&0&B(t)\\ {B}^{* }(t)&0&-\delta \tilde{{E}_{{{{\rm{z}}}}}}-J&B(t)\\ 0&{B}^{* }(t)&{B}^{* }(t)&-2\bar{{E}_{{{{\rm{z}}}}}}\end{array}\right),$$

(1)

where $\bar{{E}_{{{{\rm{z}}}}}}$ is the averaged Zeeman energy of the two qubits, $\delta {\tilde{E}}_{{{{\rm{z}}}}}=\sqrt{{J}^{2}+\delta {E}_{{{{\rm{z}}}}}^{2}}$ the effective Zeeman energy difference and B(t) the effective magnetic field induced by the EDSR. Figure 1c shows the energy levels of the four basis states. This results in four distinct transition resonance frequencies ${f}_{m,\sigma }=\bar{{E}_{{{{\rm{z}}}}}}+({c}_{\sigma }J+{c}_{m}\delta {\tilde{E}}_{{{{\rm{z}}}}})/2$ where m = 1, 2 is the qubit index and σ = ↓, ↑ is the spin with the coefficients c₁ = c_↓ = − 1, c₂ = c_↑ = + 1. By exciting one of the four transition frequencies, we implement the resonantly driven zero-controlled rotations (ZCROT) and controlled rotations (CROT)³¹. The ZCROT rotates the target qubit if the control qubit is in $\left\vert \downarrow \right\rangle$ (0 state), and the CROT rotates the target qubit if the control qubit is in $\left\vert \uparrow \right\rangle$ (1 state). The notation CROT${}_{{{{\rm{ctrl,targ}}}}}$ (ZCROT${}_{{{{\rm{ctrl,targ}}}}}$) indicates a rotation of the target qubit (targ = 1, 2) if the control qubit (ctrl = 1, 2) is in $\left\vert \uparrow \right\rangle$ ($\left\vert \downarrow \right\rangle$) state. Figure 1d shows the measured EDSR frequencies and δE_z ~ 310 MHz. We choose J = 18 MHz such that the system is in an optimal condition for high two-qubit gate fidelities¹⁸.

The effective magnetic field induced by the EDSR has the form $B(t)={f}_{{{{\rm{R}}}}}{e}^{+2i\pi {f}_{{{{\rm{MW}}}}}t}$ with f_MW the microwave driving frequency and f_R the Rabi frequency. The Rabi frequencies of both qubits are set to the same value to simplify operation. To implement the CROT₁₂ gate, where Q₁ is the control qubit, and Q₂ is the target qubit, we choose a driving frequency that is resonant with the corresponding transition frequency, i.e., f_MW = f_2,↑. By substituting B(t) into the Hamiltonian given in Eq. (1), transforming to the rotating frame (see “CROT simulation”) and neglecting far off-resonance terms using the rotating wave approximation (RWA), the Hamiltonian becomes^23,30

$${H}_{{{{{\rm{CROT}}}}}_{12}}(t)=\frac{h}{2}\left(\begin{array}{cccc}0&{f}_{{{{\rm{R}}}}}&0&0\\ {f}_{{{{\rm{R}}}}}&0&0&0\\ 0&0&0&{f}_{{{{\rm{R}}}}}{e}^{-2i\pi Jt}\\ 0&0&{f}_{{{{\rm{R}}}}}{e}^{2i\pi Jt}&0\end{array}\right).$$

(2)

The upper-left 2-by-2 sub-block provides the desired controlled-rotation, while the lower-right 2-by-2 sub-block introduces error to the gate. Choosing ${f}_{{{{\rm{R}}}}}=J/\sqrt{15}$ cancels out the population transfer caused by the lower-right sub-block for the π and the half-π CROT, but two z-phases resulting from e^±2iπJt terms will be accumulated in this sub-block. This results in a controlled-phase error which accumulates in the $\left\vert \downarrow \downarrow \right\rangle$ and $\widetilde{\left\vert \downarrow \uparrow \right\rangle }$ states^23,30. We verify this source of error using GST experiments as we discuss later. We call these phase errors the off-resonant Hamiltonian phase errors since they are errors arising from the control Hamiltonian. We change the rotating frame by offsetting the microwave phase in the pulse sequence to account for the accumulated phase errors. This allows us to correct these off-resonant Hamiltonian phase errors.

Measuring the off-resonant Hamiltonian phase error

There are four calibration sequences used to measure the off-resonant Hamiltonian phase errors, one for each controlled-rotation pulse (see “Calibration sequences”). Two of the calibration sequences for control qubit Q₁ and target qubit Q₂ are shown in Fig. 2a, b. For target qubit Q₁, the roles of Q₁ and Q₂ are swapped. The calibration sequence has three parts: First, the control qubit is prepared to the off-resonant state of the target gate, $\left\vert \uparrow \right\rangle$ for the ZCROT and $\left\vert \downarrow \right\rangle$ for the CROT. Next, we perform a Ramsey experiment with the target sequence inserted. We rotate the target qubit to the $(\left\vert \downarrow \right\rangle +\left\vert \uparrow \right\rangle )/\sqrt{2}$ state with a π/2 pulse. Then we apply the target gate of the sequence to accumulate phase error. We rotate the target qubit again to $\left\vert \uparrow \right\rangle$ using a π/2 pulse with an offset θ in phase. Finally, we measure the spin-up probability P_↑ of the target qubit at the end of the sequence. We fit the sinusoidal modulation of P_↑ as a function of θ to get the phase shift associated with each calibration sequence, as shown in Fig. 2c. The fitted phase shifts are $({\theta }_{{{{{\rm{ZCROT}}}}}_{12}},{\theta }_{{{{{\rm{CROT}}}}}_{12}},{\theta }_{{{{{\rm{ZCROT}}}}}_{21}},{\theta }_{{{{{\rm{CROT}}}}}_{21}})$$=(0.41\pm 0.025,-0.58\pm 0.02,0.43\pm 0.015,-0.49\pm 0.03)\,\,{{\mbox{rad}}}\,$, which show a distinct asymmetry between CROT₁₂ (ZCROT₁₂) and CROT₂₁ (ZCROT₂₁) sequences. We conduct simulations of the calibration sequences using the CROT Hamiltonian both with (without) using the RWA to neglect (include) the far off-resonant terms (see “CROT simulation” and Supplementary Figs. 3 and 4). We observe symmetric phase shifts when simulating with the RWA, but these phase shifts become asymmetric without the RWA. We simulate the phase shifts for different Zeeman energy difference δE_z and observe the asymmetry increases when δE_z decreases (see Supplementary Fig. 5). This indicates that the asymmetry arises from the far off-resonant terms, but further investigations are necessary.

Fig. 2: Calibration sequences for measuring the off-resonant Hamiltonian phase error.

a, b Calibration sequences used to measure off-resonant Hamiltonian phase errors for ZCROT₁₂ and CROT₁₂, where X denotes a half-π rotation. For all the sequences see Supplementary Fig. 1. c Phase shifts in the calibration sequences. The spin-up probability measured in each calibration sequences are fitted with $A\cos (\theta +{\theta }_{i})+B$ to obtain the phase shifts. With A the amplitude, B the offset, θ the phase of the second half-π pulses and θ_i the phase shift. d The off-resonant Hamiltonian phase error associated with each pulse. The phase error ϕ_m,σ associated with each transition frequency f_m,σ will accumulate in the off-resonant state when applying each pulse. Here we introduce the += (−=) operators which add (subtract) the value on the right to (from) the variable on the left, a common syntax in modern programming languages. e Schematic of compensation procedure for the off-resonant Hamiltonian phase error for the example of the calibration sequence for CROT₁₂. The phases accumulated on each basis states before the pulse is applied are shown in the columns. We then use this table to calculate the phase offset ϕ_offset and subtract this offset from the applied pulses' microwave phase to compensate for the effect of off-resonant Hamiltonian phase error. f The measured phase shifts in the calibration sequences after the phase compensation, demonstrate a significant improvement to the uncompensated case shown in b.

The Hamiltonian in Eq. (2) implies that when a CROT₁₂ gate is applied, the e^±2iπJt terms result in phases accumulated in the $\left\vert \downarrow \downarrow \right\rangle$ and $\left\vert \downarrow \uparrow \right\rangle$ states. From the full CROT Hamiltonian it follows that phase is always accumulated in the states which the pulse is not acting on (see “CROT simulation”). Figure 2d shows the relation between the four pulses and their corresponding off-resonant Hamiltonian phase errors. To obtain the relation between the fitted phase shifts and the off-resonant Hamiltonian phase errors, we write down a table of phase errors accumulated on the four basis states along the sequence and obtain a relation between fitted phase shifts and the off-resonant Hamiltonian phase errors (see “Calibration sequences”). Using this relation and the phase shifts measured, we obtain the off-resonant Hamiltonian phase errors (ϕ_1,↓, ϕ_1,↑, ϕ_2,↓, ϕ_2,↑) = (−0.07 ± 0.03, 0.14 ± 0.02, −0.07 ± 0.03, 0.12 ± 0.03)rad. We note that the phase errors are time-independent coherent errors, and therefore, we can cancel the effect by characterizing the accumulated phases.

We use the measured off-resonant Hamiltonian phase errors to compensate for the unwanted phases accumulated in the calibration sequences. Figure 2e shows the procedure we use to compensate for the phase errors in the CROT₁₂ sequence. We record all the phase errors at each step of the sequence. From these phase errors, we obtain the offset ϕ_offset needed for each pulse to compensate for the effect of phase error, which is the phase accumulated on the states the pulse is acting on (see “Calibration sequences”). To compensate for the accumulated phase error, we subtract the accumulated phase from the microwave phase, which implements a virtual z-gate²⁴. These virtual z-gates change the rotating frame according to the accumulated phase errors such that the effects on the qubit gates caused by the phase errors are canceled. Figure 2f shows the measured curves after compensating phase errors in the sequences. The fitted phase shifts after compensation are $({\theta }_{{{{{\rm{ZCROT}}}}}_{12}}^{{\prime} },{\theta }_{{{{{\rm{CROT}}}}}_{12}}^{{\prime} },{\theta }_{{{{{\rm{ZCROT}}}}}_{21}}^{{\prime} },{\theta }_{{{{{\rm{CROT}}}}}_{21}}^{{\prime} })=(0.15\pm 0.03,-0.02\pm 0.03,0.08\pm 0.04,0.01\pm 0.04)\,\,{{\mbox{rad}}}\,$. After the phase compensation, all the phase shifts are reduced to ≤0.15rad ~9^∘. We notice that there are still non-zero phase shifts in the two ZCROT sequences. This is also observed in simulation (see “CROT simulation” and Supplementary Fig. 3) from which we notice that this phase is not originating from the far off-resonant terms. This residual phase is only observed in sequences when both qubits are operated and its origin is not yet clear. A possible source for this residual phase could be a correlated gate error on Q₂ (Q₁) when applying gates acting on Q₁ (Q₂)¹⁹. Another potential source of these residual phase shifts is the AC-Stark shift. We compare our simulations with the AC-Stark shift (see Supplementary Fig. 5) and find that at low exchange coupling J the residual phase shifts ${\phi }_{{{{\rm{res}}}}}\propto {f}_{{{{\rm{R}}}}}^{2}/[2(\delta {E}_{{{{\rm{z}}}}}\pm J)]$ but deviate from the AC-Stark shift behavior at the experimental exchange coupling J = 18 MHz. This indicates that the residual phase shifts are not related to the AC-Stark shift effect, however, further investigations are required.

Compensation of the off-resonant Hamiltonian phase error

Next, we extend the use of the compensation procedure to general pulse sequences. Figure 3a shows the phase compensation procedure for general pulse sequence U₁, U₂, ..., U_N. We keep a phase error table that records the phase errors accumulated on the four basis states and check the sequence pulse by pulse with this phase error table to obtain the phase offsets. Since the errors are time-independent, we can compensate for the phase errors pulse by pulse. For each applied pulse, we check the phase error, which is accumulated on the states on which the pulse acts on and offset the microwave phase correspondingly, as done in the previous section. We then add the phase error accumulated by the pulse to the phase error table and move on to the next pulse. This procedure is performed in software before the execution of the physical pulses. We emphasize that this method can also be implemented in real-time, e.g., on an FPGA using a phase counter².

Fig. 3: Off-resonant Hamiltonian phase error compensation procedure and performance.

a General off-resonant Hamiltonian phase error compensation procedure. We check the phase error table for phases accumulated in the relevant states for each pulse (1). We then subtract the offset from the microwave phase of the pulse (2). Finally, the phase error caused by the pulse is added to the phase error table and used to obtain the offsets for the following pulses (3). b Results of two-qubit randomized benchmarking with and without the compensation procedure. The RB without the compensation procedure shows an averaged primitive gate fidelity of 97.95 ± 0.11%. The compensation procedure increases this fidelity to 99.41 ± 0.02%. The error bars represent the standard error of the mean. c, d Coefficients of the CNOT₁₂ gate error generator decomposition with and without compensation. The solid bars in the plot represent the experimental result, while the dashed bars represent the simulations. Large IZ and ZZ Hamiltonian components occur when the compensation procedure is not applied. The two dominant error terms in c are significantly reduced when applying the compensation procedure. Experiment and simulation results show good consistency. The error bars represent 1σ standard deviation from the mean.

To evaluate the performance of our calibration, we compare the pulse fidelity with and without the compensation by performing a two-qubit RB experiment^18,23. We use 15 (59) different random sequences for the experiment without (with) the phase compensation protocol (see “Two-qubit randomized benchmarking”). Figure 3b shows measured RB decays. In the run without the compensation procedure, a Clifford fidelity of 94.73 ± 0.28% is obtained, corresponding to a primitive gate fidelity of 97.95 ± 0.11%. With the compensation procedure, we achieve a Clifford fidelity of 98.48 ± 0.06%, corresponding to primitive gate fidelity of 99.41 ± 0.02%. The increase in gate fidelity demonstrates that the compensation procedure has significantly reduced the errors in the pulses.

To get a more detailed report on the performance of the quantum gates, we conduct a GST experiment^27,32 (see also “Gate-set Tomography”). Here, the GST experiment generates the two-qubit Pauli transformation matrix (PTM) of the implemented quantum gates, which describes how Pauli matrices are transformed under the quantum gate. The experimentally obtained PTM is then compared to the ideal PTM to get the error generator, which gives more specific gate error processes. By writing the error generator into a linear combination of terms representing different error processes, we can interpret the errors of our gates more intuitively³³.

Figure 3c shows the Hamiltonian projections of the CNOT₁₂ gate obtained by both experiment and simulated GST. The simulated data is obtained using an ideal Hamiltonian (see Eq. (2)) without introducing any noise (see “CROT Simulation”). Without the compensation, there are large errors in the IZ and ZZ Hamiltonian elements, both in simulation and experimental results. The consistency between the experiment and simulation shows the off-resonant Hamiltonian phase error considered in the Hamiltonian given in Eq. (2) is indeed the dominant error we measured in the experiment. The two terms are significantly suppressed when using the compensation procedure, as shown in Fig. 3d. Both experiment and simulation results exhibit this suppression, showing that the off-resonant Hamiltonian phase errors are understood and corrected as expected. The full GST gate metrics of the experiment with the phase error compensation protocol are shown in Supplementary Table 1.

After the phase compensation protocol, the CNOT₁₂ gate still has an infidelity of ~0.5%. The precision of our GST result does not allow us to make a definite statement on whether the source of this infidelity is coherent Hamiltonian errors or incoherent stochastic errors. The correlated gate error mentioned in “Measuring the off-resonant Hamiltonian phase error” could be an indication that there are still Hamiltonian errors in our gate. Further investigations are required to determine whether the CNOT₁₂ fidelity can be increased by compensating for this error.

Virtual CZ gate

Finally, we demonstrate the implementation of a virtual CZ gate with the compensation procedure, shown in Fig. 4a. In the compensation procedure, we use the phase error table to obtain the microwave phase offset for each pulse in the sequence U₁, U₂, . . . , U_N. When a π phase is added to the $\left\vert \uparrow \uparrow \right\rangle$ row, the following CROT₁₂ pulses will acquire an additional π phase in the offset while the offsets of ZCROT₁₂ pulses are unchanged. This results in a π phase difference between CROT₁₂ and ZCROT₁₂ pulses, which is effectively equivalent to a CZ₁₂ gate.

Fig. 4: Virtual CZ.

a Implementation of virtual CZ₁₂. A virtual CZ₁₂ is executed by adding a π phase to the $\left\vert \uparrow \uparrow \right\rangle$ state in the table of phase error. Other controlled z-gates CZ_ij can be implemented analogously. b Gate-set tomography result of the virtual CZ₁₂ showing the PTM obtained with experimental (solid line bars) and simulated (dashed line bars) datasets. c Comparison of stochastic noise in different gates. The graph shows the dominant stochastic error generator component IZ for the I ⊗ I, X₁ = X ⊗ I, and virtual CZ₁₂. We implement the identity gate by idling both qubits for the duration of a π/2 gate time (62 ns), and X₁ by applying a CROT₂₁ and a ZCROT₂₁ sequentially. Error bars represent the 1σ standard deviation from the mean.

To verify the virtual CZ₁₂, we perform a GST experiment with the CZ₁₂ gate-set. Figure 4b shows the estimated PTM of the virtual CZ₁₂. The measured PTM is close to the ideal CZ₁₂ and has a fidelity of 99.49 ± 0.08%, which shows that the virtual CZ₁₂ gate is well implemented. The digital phase offset needed to perform a virtual CZ operation may not be exactly π. We anticipate that by using calibration sequences similar to the CROT sequences, we can measure the actual offset and further improve the fidelity of the virtual CZ₁₂ gate.

One advantage of virtually implementing quantum gates is that the gate time is reduced to zero such that the qubits are not affected by dephasing. Figure 4c shows the IZ stochastic error component for I ⊗ I, X₁ = X ⊗ I and virtual CZ₁₂. We use the identity gate I ⊗ I, which idles both qubits for 62 ns to emulate the dephasing in a physical CZ gate. We find experimentally that IZ is the dominant component for these gates (see Supplementary Fig. 7). There is a large IZ stochastic term for the identity gate due to dephasing by residual nuclear spin or charge noise³⁴. This term is reduced in X₁ as the driven qubit is less affected by dephasing because the drive effectively acts as a filter function^4,35,36,37. For the virtual CZ₁₂, this noise is reduced to essentially zero, showing that the virtual CZ₁₂ is indeed not affected by charge noise, as expected.

In regards to the virtual CZ₁₂ gate, we note that in the GST analysis, there are two types of error generators associated with each gate: The intrinsic error generator, which commutes with the gate and the relational error generator, which does not²¹. The GST does not differentiate between relational error generators for different gates in a gate-set. Since the virtual CZ₁₂ gate is implemented virtually, its infidelity might be assigned to the other physical gates through the relational error. We observed a higher error rate in the I, X₁ and Y₁ gates for the gate-set, which includes the virtual CZ₁₂ (see Supplementary Table 2). This suggests that the error in the virtual CZ₁₂ gate might be incorrectly attributed to the physical gates, such that the actual fidelity of the virtual CZ₁₂ gate is slightly lower than stated. Additionally, we check the active and Pauli-correlation projections of the virtual CZ₁₂ gate-set (see Supplementary Fig. 7). The active generators, when combined with stochastic Pauli generators, account for T₁ relaxation process and are negligible in our result. The Pauli-correlation generators shift the error mechanism of the stochastic error. For example, changing the c_X,Z projection shifts the stochastic error from independent bit- and phase-flip error to pure dephasing in the X + Z basis³³. These correlation projections should satisfy the condition $| {c}_{P,Q}| \le \sqrt{{s}_{Q}{s}_{P}}$, where s_P, s_Q are the stochastic Pauli projections, to make the stochastic error matrix positive semidefinite³³. We observe that some of the Pauli-correlation projection terms violate this semidefinite condition in our result. These violations can be attributed to the large error bars in the stochastic projection terms or to the possibility that the GST estimation is not fully physical for this virtual CZ₁₂ gate set. Further investigation and more precise GST measurements are needed to draw further conclusions regarding this issue.

Discussion

Understanding the off-resonant Hamiltonian phase errors allows us to implement high-fidelity CROT gates systematically. With a better understanding of the origin of these phase errors, we can estimate the experimental phase shifts by numerical simulations (see Supplementary Figs. 3 and 4). The phase error compensation method also allows the implementation of a virtual CZ gate, which is useful in quantum circuits that use controlled-phase gates extensively. For example, the quantum Fourier transformation (QFT) circuit uses controlled-phase gates of several different rotation angles³⁸. Our procedure is implementable on an FPGA, which tracks and corrects the phase offsets in real-time. Such a real-time approach is crucial for quantum circuits that cannot be pre-calculated before execution, e.g., for quantum error correction^13,14 or real-time feedback initialization².

In the original proposal of the CROT gate^30,31, the exchange coupling is only turned on for the execution of the CROT and turned off for subsequent single-qubit operations. The pulse to control the exchange effectively results in a CPhase gate up to single-qubit z-rotations³⁰. This exchange coupling pulse length can be calibrated such that the CPhase gate accumulates a controlled phase of one full rotation. A microwave pulse within this exchange pulse is applied to implement a CNOT gate up to single-qubit z-rotations³⁰. In this case, we anticipate the off-resonant Hamiltonian phase errors discussed here can be canceled out by adjusting the exchange pulse time to control the accumulation of an extra-controlled phase.

The practical scalability of the exchange-always-on system remains an open question. For the three-qubit resonantly driven Toffoli gate in the exchange-controlled system, the extra conditional phase error can be removed by changing the timing of the exchange coupling pulse^13,39. This exchange pulse accumulates additional, conditional phases and has the same effect as shifting the microwave phases. In a three-qubit exchange-always-on system, keeping track of all the transition frequencies becomes more challenging, and the calibration sequences for measuring the off-resonant Hamiltonian phase errors become more complicated. While further investigations are required, we anticipate that the procedure discussed here can also be used to calibrate the controlled rotations in a three-qubit exchange-always-on system.

In summary, we demonstrated a systematic way to calibrate high-fidelity CROT gates in an exchange-always-on two-qubit system. We present a calibration procedure to compensate for the Hamiltonian off-resonant phase errors in our CROT gates, allowing us to achieve universal single and two-qubit gate fidelities above the fault-tolerant threshold of 99%. Finally, we implement a virtual CZ gate using our phase error compensation protocol.

Methods

Calibration sequences

Supplementary Fig. 1 shows all four calibration sequences and the corresponding phase error table used to obtain the phase offsets. For the ZCROT₁₂ sequence, the phase errors associated with the four states at the end of the sequence are

$${\phi }_{\uparrow \uparrow }=2{\phi }_{1,\downarrow }+2{\phi }_{2,\downarrow },$$

(3)

$${\phi }_{\uparrow \downarrow }=-2{\phi }_{1,\downarrow },$$

(4)

$${\phi }_{\downarrow \uparrow }=2{\phi }_{1,\uparrow }-2{\phi }_{2,\downarrow },$$

(5)

$${\phi }_{\downarrow \downarrow }=-2{\phi }_{1,\uparrow }.$$

(6)

The Ramsey sequence at the end measures the relative phase between the two off-resonant states of ZCROT₁₂, the $\left\vert \uparrow \downarrow \right\rangle$ and $\left\vert \uparrow \uparrow \right\rangle$ state. Thus, the measured phase shift is

$${\theta }_{{{{{\rm{ZCROT}}}}}_{12}}={\phi }_{\uparrow \downarrow }-{\phi }_{\uparrow \uparrow }=-4{\phi }_{1,\downarrow }-2{\phi }_{2,\downarrow }.$$

(7)

Using a similar argument, we can write the phase shifts measured into a linear combination of the off-resonant Hamiltonian phase errors

$${\theta }_{{{{{\rm{ZCROT}}}}}_{12}}=-4{\phi }_{1,\downarrow }-2{\phi }_{2,\downarrow },$$

(8)

$${\theta }_{{{{{\rm{CROT}}}}}_{12}}=-4{\phi }_{1,\uparrow },$$

(9)

$${\theta }_{{{{{\rm{ZCROT}}}}}_{21}}=-2{\phi }_{1,\downarrow }-4{\phi }_{2,\downarrow },$$

(10)

$${\theta }_{{{{{\rm{CROT}}}}}_{21}}=-4{\phi }_{2,\uparrow }.$$

(11)

Solving these four equations gives the explicit form of the off-resonant Hamiltonian phase errors. The relation is

$$({\phi }_{1,\downarrow },{\phi }_{1,\uparrow },{\phi }_{2,\downarrow },{\phi }_{2,\uparrow })$$

(12)

$$=\left(\frac{-2{\theta }_{{{{{\rm{ZCROT}}}}}_{12}}+{\theta }_{{{{{\rm{ZCROT}}}}}_{21}}}{6},-\frac{{\theta }_{{{{{\rm{CROT}}}}}_{12}}}{4},\frac{{\theta }_{{{{{\rm{ZCROT}}}}}_{12}}-2{\theta }_{{{{{\rm{ZCROT}}}}}_{21}}}{6},-\frac{{\theta }_{{{{{\rm{CROT}}}}}_{21}}}{4}\right).$$

(13)

With the obtained off-resonant Hamiltonian phase errors, we write down a table of phase errors accumulated on each basis state before the pulse is applied. We calculate the offsets needed by

$${\phi }_{{{{\rm{offset}}}},ZCRO{T}_{12}}={\phi }_{\downarrow \downarrow }-{\phi }_{\downarrow \uparrow },$$

(14)

$${\phi }_{{{{\rm{offset}}}},CRO{T}_{12}}={\phi }_{\uparrow \downarrow }-{\phi }_{\uparrow \uparrow },$$

(15)

$${\phi }_{{{{\rm{offset}}}},ZCRO{T}_{21}}={\phi }_{\downarrow \downarrow }-{\phi }_{\uparrow \downarrow },$$

(16)

$${\phi }_{{{{\rm{offset}}}},CRO{T}_{21}}={\phi }_{\downarrow \uparrow }-{\phi }_{\uparrow \uparrow }.$$

(17)

Two-qubit randomized benchmarking

We choose sequence lengths L = (1, 8, 16, 23, 31) in our two-qubit randomized benchmarking experiment. For each length, we use 59 (15) different random sequences for the experiment with (without) the phase compensation protocol. We combined three datasets measured over a time span of one week, demonstrating the stability of our qubits. For each sequence, the probability is obtained by averaging 150 single-shot measurements. The gates in each sequence are randomly chosen from the two-qubit Clifford group, which contains 11520 elements⁴⁰. We use a computer search to find the combinations of primitive gates (see Supplementary Fig. 2) to construct all two-qubit Clifford group elements^18,23. At the end of the sequence, we search for the recovery gate, which projects the state into the target state $\left\vert \uparrow \uparrow \right\rangle$ or $\left\vert \downarrow \downarrow \right\rangle$. This results in two sequence fidelities F_↑↑(n) and F_↓↓(n). We fit the difference between two sequences F(n) = F_↑↑(n) − F_↓↓(n) with the formula F(n) = (A_t − B_t)pⁿ where (A_t − B_t) is the visibility and absorbs the SPAM error and p is the depolarizing strength. The two-qubit Clifford gate fidelity is obtained by F_C = (1 + 3p)/4. Each Clifford element is composed of 2.57 primitive gates on average. We, therefore, calculate the primitive gate fidelity as F_p = 1 − (1 − F_C)/2.57.

CROT simulation

We start with the Hamiltonian given in Eq. (1) and transform the Hamiltonian into the rotating frame using

$${H}_{R}(t)=RH{R}^{{\dagger} }-\frac{ih}{2\pi }\frac{\partial R}{\partial t}{R}^{{\dagger} },$$

(18)

with $R=\,{{\mbox{diag}}}\,({e}^{-2i\pi {E}_{{{{\rm{z}}}}}t},{e}^{-i\pi (-\delta {\tilde{E}}_{{{{\rm{z}}}}}-J)t},{e}^{-i\pi (\delta {\tilde{E}}_{{{{\rm{z}}}}}-J)t},{e}^{2i\pi {E}_{{{{\rm{z}}}}}t})$. The Hamiltonian in the rotating frame is then

$${H}_{R}(t)=\frac{h}{2}\left(\begin{array}{cccc}0&B(t){e}^{-2i\pi {f}_{2,\uparrow }t}&B(t){e}^{-2i\pi {f}_{1,\uparrow }t}&0\\ {B}^{* }(t){e}^{2i\pi {f}_{2,\uparrow }t}&0&0&B(t){e}^{-2i\pi {f}_{1,\downarrow }t}\\ {B}^{* }(t){e}^{2i\pi {f}_{1,\uparrow }t}&0&0&B(t){e}^{-2i\pi {f}_{2,\downarrow }t}\\ 0&{B}^{* }(t){e}^{2i\pi {f}_{1,\downarrow }t}&{B}^{* }(t){e}^{2i\pi {f}_{2,\downarrow }t}&0\end{array}\right),$$

(19)

with the effective EDSR magnetic field $B(t)={f}_{{{{\rm{R}}}}}{e}^{+2i\pi {f}_{{{{\rm{MW}}}}}t+i\phi }$. We substitute this magnetic field into the rotating frame Hamiltonian and calculate the propagator. If the RWA is used, we set the elements in the far-off-resonant terms to zero before calculating the propagator.

We choose J = 18 MHz and ${f}_{{{{\rm{R}}}}}=J/\sqrt{15}\simeq 4.64$ MHz, which results in a π/2 gate time T_π/2 ≃ 53.8 ns. We compute the unitary propagator with this Hamiltonian by

$$\begin{array}{r}U({f}_{{{{\rm{MW}}}}},\phi )={{{\mathcal{T}}}}\exp \left(-\frac{i}{\hslash }\int\nolimits_{0}^{{T}_{\pi /2}}H({f}_{{{{\rm{MW}}}}},\phi ,t)dt\right),\end{array}$$

(20)

with ${{{\mathcal{T}}}}$ the time-ordering operator. By choosing the driving frequency f_MW, we select which ZCROT or CROT is implemented. Changing the microwave phase ϕ changes the rotation angle of the pulse. This unitary is then used for simulating the implemented pulses.

Gate-set tomography

For the GST experiments, depending on the implemented gates in the system, a different target gate-set is chosen. This target gate-set is then used to compose a preparation and measurement gate-set and a set of germ sequences. The preparation- and measurement-fiducial gates are used to make tomographic measurements. These fiducial gates must be able to prepare and measure an information-complete set of states. The germ sequence in between is chosen from the germ set, which is amplificationally complete²⁷ and, therefore capable of amplifying all possible errors that can occur during the gate operation.

We perform GST with the python package pyGSTi³². We use the default gate set provided by the pyGSTi package and the fiducial pair reduction function to reduce the number of sequences required. The CNOT₁₂ gate-set contains {X₁, Y₁, X₂, Y₂, CNOT₁₂}. The identity gate I is implemented by idling both qubits for a time of T_π/2 = 62 ns. X_1,2 (Y_1,2) are π/2 rotations along the x-axis (y-axis) for Q₁ or Q₂, respectively. The 15 germs for this gate-set are {I, X₁, Y₁, X₂, Y₂, CNOT₁₂, X₁Y₁, X₂Y₂, X₁X₁X₁, X₂X₂X₂, CNOT₁₂X₂X₁X₁, X₁X₂Y₂X₁Y₂Y₁, X₁Y₂X₂Y₁X₂X₂, Y₁Y₂X₁Y₁X₁CNOT₁₂, Y₁X₂Y₂X₁X₂X₁Y₁Y₂}, and the fiducial gates {null, X₂, Y₂, X₂X₂, X₁, X₁X₂, X₁Y₂, X₁X₂X₂, Y₁, Y₁X₂, Y₁Y₂, Y₁X₂X₂, X₁X₁, X₁X₁X₂, X₁X₁Y₂, X₁X₁X₂X₂}. In contrast to the identity gate I, the null gate has no physical idling time. We choose the sequence lengths L = (1, 2, 4, 8, 16), which results in a total of 1760 sequences. For the CZ₁₂ gate-set which contains { I, X₁, Y₁, X₂, Y₂, CZ₁₂}, the germs and fiducial gates are { I, X₁, Y₁, X₂, Y₂, CZ₁₂, X₁Y₁ X₂Y₂, X₁X₁Y₁, X₂Y₂CZ₁₂, CZ₁₂X₂X₁X₁, X₁X₂Y₂X₁Y₂Y₁, X₁Y₂X₂Y₁X₂X₂, CZ₁₂X₂Y₁CZ₁₂Y₂X₁,Y₁X₁Y₂X₁X₂X₁Y₁Y₂ }, and {null, X₂, Y₂, X₂X₂, X₁, X₁X₂, X₁Y₂, X₁X₂X₂, Y₁, Y₁X₂, Y₁Y₂, Y₁X₂X₂, X₁X₁, X₁X₁X₂, X₁X₁Y₂, X₁X₁X₂X₂ }, which results in a total of 1644 sequences. All the gates used in the GST experiment are composed of CROT and ZCROT π/2 pulses and single-qubit z-rotations (see Supplementary Fig. 6). The sequences are executed on the device to gather outcome counts. After execution of these sequences, the measured spin-up and spin-down counts are analyzed with an H+S model (see “Error generators”) to obtain the PTMs ${G}_{\exp }$ of the gates. This PTM has the form

$${({G}_{\exp })}_{ij}=\frac{1}{d}\,{{\mbox{tr}}}\,[{P}_{i}G({P}_{j})],$$

(21)

where d is the Hilbert space dimension and P_i are the two-qubit Pauli operators. The estimated PTMs are then compared with the ideal PTMs to obtain the error generators through functions in the pyGSTi package.

To verify the assumption we made for the off-resonant Hamiltonian phase error, we also perform GST with simulated datasets. First, we take the sequences used in the experiment and calculate the corresponding series of unitary propagators with the ideal Hamiltonian. Then, we evolve the input ground state with this series of unitaries to obtain the final output state and calculate probabilities in each outcome to generate simulated counts. Finally, the simulated counts are analyzed in the same way as the experimental counts.

Error generators

For a noisy implementation ${G}_{\exp }$ of the ideal quantum gate G_ideal, we can model the imperfect gate as

$${G}_{\exp }={{{\mathcal{E}}}}{G}_{{{{\rm{ideal}}}}},$$

(22)

which is an ideal quantum gate followed by some noise process ${{{\mathcal{E}}}}$. By inverting the ideal gate, we get the noise process as

$${{{\mathcal{E}}}}={G}_{\exp }{G}_{{{{\rm{ideal}}}}}^{-1}.$$

(23)

If we take the logarithm of this noise process and assume that noise is small i.e., ${{{\mathcal{E}}}}\simeq I$. Using the approximation $\log X\simeq (X-I)$ with small (X−I) we get the error generator³³

$$L=\log ({G}_{\exp }{G}_{{{{\rm{ideal}}}}}^{-1})=\log {{{\mathcal{E}}}}\simeq {{{\mathcal{E}}}}-I,$$

(24)

which is the approximated difference between the noise process ${{{\mathcal{E}}}}$ and the identity. If the gate is noise-free, i.e., ${{{\mathcal{E}}}}=I$, then L = 0. This error generator can be written into a linear combination

$$L={L}_{H}+{L}_{S}+{L}_{C}+{L}_{A}$$

(25)

$$=\mathop{\sum}\limits_{P}{h}_{P}{H}_{P}+\mathop{\sum}\limits_{P}{s}_{P}{S}_{P}$$

(26)

$$+\mathop{\sum}\limits_{P,Q \,> \,P}{c}_{P,Q}{C}_{P,Q}+\mathop{\sum}\limits_{P,Q \,>\, P}{a}_{P,Q}{A}_{P,Q}.$$

(27)

The terms in the linear combination correspond to error generators representing different error processes. The error generators are divided into four categories, Hamiltonian generator H_P, stochastic Pauli generator S_P, Pauli-correlation generator C_P,Q and active generator A_P,Q. We use the H+S model of pyGSTi package^21,32, which only contains Hamiltonian and stochastic Pauli errors which have clear physical meanings. The Hamiltonian error generators represent a systematic over- or under-rotation of the qubit state on the Bloch sphere in one of the rotation axes. On the other hand, the stochastic Pauli generators represent the contraction to one of the axes of the qubit Bloch sphere. The coefficient of these error generator terms is obtained by³³

$${h}_{P}=-\frac{i}{{d}^{2}}\,{{\mbox{Tr}}}\,\left[(P\otimes I-I\otimes P)L\right],$$

(28)

$${s}_{P}=\frac{1}{{d}^{2}}\,{{\mbox{Tr}}}\,\left[(P-I)L\right],$$

(29)

where P is the two-qubit Pauli matrices. We extract these coefficients using internal functions in the pyGSTi package. These coefficients can be used to calculate the Jamiolkowski probability ϵ_J(L) and the Jamiolkowski amplitude θ_J(L), which gives the amount of incoherent and coherent errors, respectively. For an error generator L being decomposed into list of {h_P, s_P} coefficients, these two metrics are³³

$${\epsilon }_{J}(L)=\,{{\mbox{tr}}}\,[{\rho }_{J}(L)(I-\left\vert {{\Psi }}\right\rangle \left\langle {{\Psi }}\right\vert )]=\mathop{\sum}\limits_{P}{s}_{P},$$

(30)

$${\theta }_{J}(L)=\parallel (I-\left\vert {{\Psi }}\right\rangle \left\langle {{\Psi }}\right\vert ){\rho }_{J}(L)\left\vert {{\Psi }}\right\rangle \parallel ={\left(\mathop{\sum}\limits_{P}{h}_{P}^{2}\right)}^{1/2}.$$

(31)

The Jamiolkowski probability and Jamiolkowski amplitude can be used to approximate the averaged gate infidelity related to error generator L. For small errors, the approximated average gate infidelity is³³

$$r=\frac{d}{d+1}[{\epsilon }_{J}(L)+{\theta }_{J}{(L)}^{2}].$$

(32)