Introduction

One of the most important components of water resource planning and management is the responsible operation of reservoirs and dams for a range of economic, social, and cultural reasons. This is due to the significant rule it plays in the availability of water. Many of the optimization problems that arise in engineering sciences are inherently complicated and demanding, making conventional optimization methodologies, like mathematical programming methods, inadequate for handling them. In this regard, several scholars have built a collection of evolutionary algorithms. To put it simply, these researchers are trying to find an efficient and successful operation method within the search space by integrating the basic concepts of operation techniques. These methods are currently frequently called exploratory technologies (Blum and Roli 2003; Nicklow et al. 2010). Among evolutionary algorithms, the genetic algorithm is thought to be the most widely used technique (Chang et al. 2005; Momtahen and Dariane 2007).

Multi-objective metaheuristic algorithms are a practical tool for system optimization in the field of water resources (Zarei et al. 2022; Karamian et al. 2023; Rezaei and Safavi 2020).

The non-dominated sorting genetic algorithm (NSGA-II), which is essentially a kind of multi-objective genetic algorithm, uses a population of possible solutions to go through each step of the solution process. Compared to the standard genetic algorithm model, this approach converges more quickly (Deb et al. 2002; Azari et al. 2018; Zeinali et al. 2020). This is because the model chooses solutions that are not dominated each time the equations are repeated and has an appropriate structure. This approach is used in this study to carry out the optimization procedure. This is because there are many choice factors involved, the problem is complex, and the structure is multi-objective. Multi-objective genetic algorithm was used by Jian et al. (2005) in their study on programming of multi-reservoir systems. Despite the fact that the evolutionary algorithm adds more variables and lengthens the program’s execution time, they found that it has a great potential for handling issues with few inputs and complex circumstances. Goorani and Shabanlou (2021) used NSGA-II to extract the optimal rule curve and establish the optimal operation of the Marun dam in order to meet both quantitative and qualitative goals.

As was previously indicated in this debate, a great deal of research has been done on the topic of enhancing reservoir operation through deterministic optimization. In many researches, the structure of multi-objective optimization (deterministic optimization) based on recorded historical inputs has been used to optimize the operation of water resources systems. This type of optimization takes into account a specific sequence of inflows into the reservoir across the operation period, and the release from the reservoir is optimized to supply the downstream uses under these conditions. The issue with these models is that the best answers are not transferable to other potential reservoir inflow scenarios. Moreover, the acquired optimal solutions are probably not going to work if the inflow to the reservoirs changes, so the system’s operation should be improved again using an optimization method. One solution to this kind of problem, according to Bayesteh and Azari (2021) and Jalilian et al. (2022), is to use stochastic optimization to take advantage of random inflows. However, in order to avoid extending the solution time due to the variety of the inflow series, this strategy necessitates a large reduction in the number of decision factors. This will lead to issues with the system’s real-time functionality. Using intelligent techniques is another option for implementing the results of system optimization in real time.

In recent research, along with statistical methods (Ebtehaj et al. 2020; Zeynoddin et al. 2020; Azari et al. 2021), in some studies, machine learning-based methods and hybrid methods are used to predict hydroclimatological data, river flow and changes in groundwater storage have been used (Nourmohammadi Dehbalaei et al. 2023; Soltani et al. 2021; Esmaeili et al. 2021).

The support vector machine, which served as the foundation for the development of regression vector machine technology, has been applied in several researches to predict time series. Lin et al. (2006) discovered that support vector machines outperformed ARMA and artificial neural network models in the forecasting of flow rate time series. Support vector machines and particle swarm algorithms were two of the many methods used by Du et al. (2017) to anticipate the three-hour rainfall at a meteorological station in Nanjing, China. Su et al. (2014) used GA-SVM in their work to predict the monthly storage volume of China’s Miyun Reservoir. Lei et al. (2021) stated that the combined GA-SVM model has been used in several researches to improve the accuracy of the hydrological parameter analysis.

Zeynoddin et al. (2020), Azari et al. (2021), Poursaeid et al. (2020, 2021, 2022), Yosefvand and Shabanlou (2020), Malekzadeh et al. (2019a, b), Azimi et al., (2020), Azizpour et al. (2021, 2022), Mazraeh et al. (2023, 2024), Fallahi et al., (2023), Mohammad et al. (2023), Azizi et al., (2023), Amiri et al, (2023) and Soltani and Azari (2023) stated that using artificial intelligence technologies and stochastic models to predict changes in groundwater storage and meteorological and hydrological parameters is one of the most widely used strategies in water resources planning (Soltani and Azari, 2022; Zeynoddin et al. 2018; Nourmohammadi Dehbalaei et al. 2023; Esmaeili et al. 2021). Hybrid models and machine learning-based techniques like GMDH, ORELM, and ELM have been extensively utilized recently to forecast hydroclimatological parameters including discharge and precipitation in diverse basins. Among these techniques were hybrid models. Group method of data handling (GMDH) has been used to simulate different problems such as discharge coefficient (Gharib et al. 2020; Moghadam et al. 2022; Shabanlou Saeid 2018; Khani and Shabanlou 2022; Shahbazbeygi et al. 2021) and hydraulic jump (Azimi et al. 2018).

The current research is based on a combination of the MOPSO multi-objective algorithm with innovative machine learning techniques, like GSGMDH, SAELM, and ORELM. This is done to make sure that the dam can be run as effectively as feasible in the present. In this example, real recorded data is used for system optimization instead of randomly generated data. Then, based on the operational conditions, the optimal rules that were produced throughout the optimization process are updated in real time. Deep learning techniques are employed to achieve this goal. In this specific scenario, there is a significant relationship between the optimal release rate variable (as a dependent variable) and the monthly inflows to the reservoir, the volume of water stored in the reservoir, changes in the volume of the reservoir, and downstream needs (as independent variables). Once the procedure is completed and the optimal variables are extracted, this association is established. Therefore, the main goal of this research is to effectively integrate the MOPSO optimization algorithm with deep learning techniques like GSGMDH, SAELM, and ORELM in order to achieve the most efficient operation of the dam in real time. In this scenario, real-time calculations of the first four parameters at the beginning of each month will be used to determine the ideal amount of release from the dam, accounting for variations in inflows over the next few years. But with this structure, understanding the optimal parameters does not require running optimization again. This is due to the fact that, with the anticipated change in the reservoir’s intake over the next several years, the optimization procedure needs to be carried out again in the shared structure and using the deterministic optimization approach. Rather, deep learning techniques can be used to obtain the optimal release quantity in real time. This is dependent on the reservoir’s inflows and initial water storage level, as well as changes in the reservoir’s storage over the course of the month and downstream demands. The innovation of the current research is the combined use of the MOPSO algorithm and the new machine learning model (GSGMDH) for the optimal exploitation of water resources systems in real time. Based on this innovation, the rules for the operation of the dam command curve in the future time are based on the data new ones can be extracted instantly and there is no need to run the optimizer algorithm again.

Methods and materials

Study area

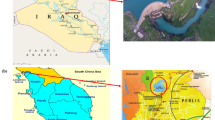
In particular, the Ilam dam, located in the semi-arid and desert region of western Iran, would be the site of this investigation. The three sub-basins that comprise the base of the basin area of this dam are Gol-Gol, Chaviz, and Emma. The main river that pours into the dam, the Konjancham River, is split into two smaller rivers, Chaviz and Gol-Gol, as Fig. 1 illustrates. The Ilam dam provides drinking water to the city of Ilam and the agricultural areas of Amirabad and Konjancham. River data and maps, exact locations of hydrometric stations and dams, and a range of applications are defined in the WEAP model (Fig. 1). The amount of water entering the system is equal to the discharge values that have been observed upstream of the Ilam dam and at the dam location over 30 years, or 366 months.

Fig. 1
figure 1

Location of study area, dam, and rivers and schematic of WEAP model

Full size image

The simulation of the system

Using available resources and adhering to basic GIS maps, the WEAP model digitizes various types of information, including the course of rivers, locations of hydrometric stations, dam sites, water withdrawal channels, nodes linked to cities and uses, and other data. The model also includes irrigation data time series, agricultural, drinking, and environmental use quantities, reservoir management parameters, water withdrawal sites, and any other relevant data. The Tennant (1976) method, which is one of the hydrological grading methods, is utilized to approximate the minimum downstream environmental flow based on the natural flow of the river. In Tennant method, 30 and 10% of the average annual flow, respectively, is considered as the minimum environmental flow in the first and second six months of the year. Table 1 lists the most important operational characteristics for the Ilam dam.

Table 1 Ilam dam operating parameters during operation
Full size table

The values of the inflows that are deposited into the reservoir of the Ilam dam are computed using the model-defined flow rate values of the rivers that are situated upstream of the dam at the Chaviz, Gol-Gol, and Emma hydrometric stations. The average amount of precipitation that fell in these areas over the course of the machine’s simulation period is shown in Fig.  2a. The model specifies the environmental requirements for the downstream areas as well as the water demands of the areas immediately downstream of the Ilam dam, which include the plains of Amirabad and Konjancham. It also specifies a portion of the drinking water requirements of the city of Ilam. The monthly usage statistics are shown for your review in Fig. 2b.

Fig. 2
figure 2

a Average monthly discharge at hydrometric stations upstream the dam b monthly agricultural, drinking, and environmental demand values downstream the dam (MCM)

Full size image

Simulator model structure

The WEAP model was used to simulate system performance. This model is used in many researches to simulate surface and groundwater systems (Karamian et al. 2023; Goorani and Shabanlou 2021). In WEAP model, the simulation period was considered to be about 30 years. The other parameters in the WEAP model included time series parameters of hydrologically recorded data and information on monthly demands (agricultural, drinking, and environmental demands), information on reservoirs and places of withdrawal, coefficients and required parameters, etc., which are mostly in the form of text files (CSV file) and according to the instructions for setting the input files were prepared and introduced to the model using the auto-call feature in the model functions section.

The proposed multi-objective operation model’s structure

The MOPSO multi-objective approach is used in the context of this inquiry to optimize the system. A multi-objective function is used to evaluate the quality of the solutions at each iteration of the optimization process. First, the goal is to meet as many system requirements as possible in percentage terms. Secondly, the goal is to minimize the amount of penalty that results from exceeding the reservoir’s permissible capacity during the whole operation period.

Objective functions

  1. 1.

    Optimizing the overall coverage percentage for every demand in the system

    $$ F_{1} = {\text{Maximize}}\left( {\mathop \sum \limits_{z = 1}^{m} \mathop \sum \limits_{d = 1}^{k} \mathop \sum \limits_{t = 1}^{n} \left( {{\text{COV}}_{zdt} } \right)} \right) = {\text{Maximize}}\left( {\mathop \sum \limits_{z = 1}^{m} \mathop \sum \limits_{d = 1}^{k} \mathop \sum \limits_{t = 1}^{n} \left( {\frac{{{\text{TDW}}_{zdt} }}{{{\text{MD}}_{zdt} }}} \right)} \right) $$
    (1)

This study extends the structure of the MOPSO algorithm for determining the goal functions’ minimum values. Consequently, Eq. (1) is recast as Eq. (2):

$$ F_{1} = {\text{Minimize}}\left( {\mathop \sum \limits_{z = 1}^{m} \mathop \sum \limits_{d = 1}^{k} \mathop \sum \limits_{t = 1}^{n} \left( {(1 - {\text{COV}}_{zdt} } \right)} \right) = {\text{Minimize}}\left( {\mathop \sum \limits_{z = 1}^{m} \mathop \sum \limits_{d = 1}^{k} \mathop \sum \limits_{t = 1}^{n} \left( {1 - \frac{{{\text{TDW}}_{zdt} }}{{{\text{MD}}_{zdt} }}} \right)} \right) $$
(2)

where COVzdt is the percentage of each time t that the demand d in the zone z is supplied. TDWzdt: The total amount of water provided for each time t in relation to demand d in zone z. MDzdt: The volume of water needed at each moment t to meet demand d in zone z.

  • 2.The second aim function is to minimize the quantity of violations of the reservoir’s permitted operating capabilities.

    $$ F_{2} = {\text{Minimize}}\left( {\mathop \sum \limits_{R = 1}^{k} \mathop \sum \limits_{t = 1}^{n} {\text{Max}}\left( {\left( {1 - \frac{{S_{tR} }}{{S_{{\min_{R} }} }}} \right),0} \right)} \right) $$
    (3)

    where \({S}_{tR}\): the amount of water stored at any one time t in the dam reservoir R, \({S}_{{min}_{R}}\):the amount of water stored in reservoir R at the dam while it is operating at its lowest capacity.

Limitations:

$$ {\text{TAW}}_{tzs} = {\text{RS}}_{tzs} ,\;t = 1,...,m \times y,\;z = 1,...,nz\;s = 1, \ldots ,ns $$
(4)

\({\text{RS}}_{tzs}\): The total amount of water allotted by zone z to sector s at each time t, \(nz\): the total number of demand areas, \(ns\): the number of various water consumers in each demand area, \(m\): the number of months, \(y\): the number of operation years

$$ {\text{ARS}}_{tzs} = \left\{ {\begin{array}{*{20}c} {{\text{DM}}_{tzs} } & {{\text{if}}\left( {{\text{TSR}}_{t} - \sum\limits_{z = 1}^{z - 1} {\sum\limits_{s = 1}^{s} {{\text{DM}}_{tzs} - \sum\limits_{z = 1}^{z} {\sum\limits_{s = 1}^{s - 1} {{\text{DM}}_{tzs} } } } } } \right) \ge {\text{DM}}_{tzs} } \\ {\left( {{\text{TSR}}_{t} - \sum\limits_{z = 1}^{z - 1} {\sum\limits_{s = 1}^{s} {{\text{DM}}_{tzs} - \sum\limits_{z = 1}^{z} {\sum\limits_{s = 1}^{s - 1} {{\text{DM}}_{tzs} } } } } } \right)} & {{\text{otherwise}}} \\ \end{array} } \right\} $$
(5)
$$ Z = {\text{IZ}}(1), \ldots ,{\text{IZ}}(nz)\;\;S = {\text{IS}}(1), \ldots ,{\text{IS}}(ns) $$

\({\text{ARS}}_{tzs}\): the entire volume of surface water from zone z that is allotted to sector s in time z (taking demand priority of consumptions into consideration)

$$ {\text{TDF}}_{tzs} = {\text{DM}}_{tzs} - {\text{ARS}}_{tzs} $$
(6)

\({\text{TDF}}_{tzs}\):The amount of water scarcity experienced by customers in zone z during each time interval t

$$ M1 < Tb1 < N1 $$
(7)

\(Tb1\): The Ilam dam’s hedging level (m), \(M1\): operation dead level (m), \(N1\): the operation maximum level of the Ilam dam (m).

The MOPSO algorithm’s main body consists of twenty-four decision criteria. Twelve variables are linked to the capacity of the reservoir at the hedging level, and twelve variables are linked to the hedging factor—which is defined in the system on a monthly basis.

Machine learning methods (ML)

The results of the optimization method enable the determination of the ideal rule curve or dam release rate using the observed inflows as a base. When they are really running the reservoir system, the operators usually adhere to the rule curves. They can then use this information to make reasonably accurate decisions about how to run the reservoirs in a range of scenarios. The duty curve is an illustration of the amount of storage or discharge that the reservoir needs to have during a given time of the year (often a month). Because the operation rule curves provide a set of specific and rigid guidelines, operators are thus able to make appropriate decisions about releases in real time, taking it into account and anticipating future flows. In order to update the optimization rules for real-time settings, this inquiry makes use of the generalized structure of group method of data handling (GSGMDH). Next, a comparison is drawn between this model’s performance and other machine learning techniques, such ORELM and SAELM, among others.

Generalized structure of group method of data handling (GSGMDH)

These straightforward structures are gradually combined to create a complicated system with good performance (Elkurdy et al. 2021; Naderpour et al. 2020). One modeling and linear regression technique that is employed is the GMDH. Rather than creating estimation models all at once, an incremental and iterative technique is employed. This approach is used to build estimating models and involves the creation and addition of very basic structures called polynomial neurons. The GMDH neural network, according to Zaji et al. (2018), Miri et al. (2021), and Ahmadi et al. (2019), is composed of a group of neurons that are formed by connecting different pairs of neurons with a polynomial of the second degree. A collection of inputs is used to characterize the estimated function \(\hat{f}\) with the output \(\hat{y}\)

$$ X \, = \, \left( {x_{1} , \, x_{2} , \, x_{3} , \ldots , \, x_{n} } \right) $$
(8)

with the fewest errors in relation to the actual output, y. That being said, the connection for M laboratory data, which consists of n inputs and one output, presents the real results as follows:

$$ y_{i} = f(x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} ,)\quad (i = 1,2, \ldots ,M) $$
(9)

We are trying to find a network that can figure out the output value for every vector X that is present in the input:

$$ \hat{y}_{i} = \hat{f}(x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} ,)\quad (i = 1,2, \ldots ,M) $$
(10)

The following should be noted in order to lower the mean square error (MSE) between the actual values and the predicted values:

$$ {\text{MSE}} = \frac{{\sum\limits_{i = 1}^{M} {(\hat{y}_{i} - y_{i} )^{2} } }}{M} \to {\text{Min}} $$
(11)

The following polynomial function can be used to define the form of link between the input and output variables (Dag and Yozgatligil 2016; Mallick et al. 2020; Elkurdy et al. 2021).

$$ y = a_{0} + \sum\limits_{i = 1}^{K} {a_{i} } x_{i} + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {a_{ij} } } z_{i} z_{j} + \cdots + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {a_{ijk} } } } + \cdots $$
(12)

The following relationship is one of the many real-world scenarios in which the quadratic and two-variable form of this polynomial is employed:

$$ \hat{y} = G(x_{i} ,x_{j} ) = a_{0} + a_{1} x_{i} + a_{2} x_{j} + a_{3} x_{i}^{2} + a_{4} x_{j}^{2} + a_{5} x_{i} x_{j} $$
(13)

Using regression techniques, the unknown coefficients ai derived in the following relationship are constructed in order to minimize the difference between the actual output y and the calculated values for each pair of the input variables xi and yi. Equation 12 is used to generate a set of polynomials, and all of the unknown coefficients can be determined using the least squares method (LSM). The coefficients of each neuron’s equations are found to minimize the neuron’s total error for each Gi function, which stands in for each produced neuron. The goal of doing this is to match inputs as closely as possible across all potential pairs of input–output sets.

$$ E = \frac{{\sum\limits_{i = 1}^{M} {(y_{i} - G_{i} )^{2} } }}{M} \to {\text{Min}} $$
(14)

One of the core techniques of the GMDH algorithm, the least squares approach, can be used to obtain the unknown coefficients of every neuron. Using n input variables, all binary combinations—also referred to as neurons—are built. Next,

$$\left(\begin{array}{c}n\\ 2\end{array}\right)=\frac{n(n-1)}{2}$$

The following equation can be used to represent the second layer, which is where neurons are built:

$$ \left\{ {\left. {(y_{i} ,x_{ip} ,x_{iq} )} \right|(i = 1,2, \ldots ,M)\;\& \;p,q \in (1,2, \ldots ,M)} \right\} $$
(15)

We use the function expressed in Eq. 14’s quadratic form to determine the value of each M triple row. These equations can be written as the following relation when put in matrix form:

$$ Aa = Y $$
(16)

The following is the equation for the quadratic equation given in Eq. 13, where A is the vector of unknown coefficients:

$$ a = \left\{ {a_{0} ,a_{1} ,...,a_{5} } \right\} $$
(17)
$$ Y = \left\{ {y_{1} ,y_{2} ,y_{3} ,...,y_{M} } \right\}^{T} $$
(18)

It is evident from the function’s form and the values of the input vectors that:

$$ G = \left[ {\begin{array}{*{20}c} 1 & {x_{1p} } & {x_{1q} } & {x_{1p} x_{1q} } & {x_{1p}^{2} } & {x_{1q}^{2} } \\ 1 & {x_{2p} } & {x_{2q} } & {x_{2p} x_{2q} } & {x_{2p}^{2} } & {x_{2q}^{2} } \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & {x_{Mp} } & {x_{Mq} } & {x_{Mp} x_{Mq} } & {x_{Mp}^{2} } & {x_{Mq}^{2} } \\ \end{array} } \right] $$
(19)

The equations’ solution in the following form is provided by the least squares method of multiple regression analysis:

$$ a = (A^{T} A)^{ - 1} A^{T} Y $$
(20)

The vector of coefficients for each of the M sets of three that are accessible is computed by this equation. The coefficients of neurons in the hidden and output layers during the training phase are also determined by the researcher’s intended confidence interval and the program’s initial specification of the degree of significance. This is also where the data screening mechanism—which entails removing variables that exhibit poor correlation at this phase—and the optimization of the neuronal coefficients and equations are completed.

Large-scale calculations are practically solvable, allowing the system of normal equations to be set under adequate and solvable conditions (Naderpour et al. 2020; Park et al. 2020; Ahmadi et al. 2019). The main benefit of the GMDH above conventional neural networks is the ability to develop and provide a mathematical model for the process under study using polynomials (Madala and Ivakhenko 1994). The GMDH’s great capability for multi-parameter data set analysis is an additional benefit (Dodangeh et al. 2020). It can also automatically determine the model’s structure and parameters (Stepashko et al. 2017), as well as exclude inputs that have a negligible impact on the output value computation (Dag et al. 2016; Park et al. 2020).

Furthermore, even though classical GMDH has many advantages—for example, automatically choosing the most efficient input variables, automatically determining the model’s structure, and taking into account both simplicity and accuracy at the same time to prevent overfitting-it also has several drawbacks that make it challenging to use. (1) The polynomial degree is limited to two; (2) each neuron’s input is limited to two; and (3) each neuron’s input is limited to the neurons in the layer adjacent to it. These are the principal issues that are related to this approach. The MATLAB software is being used to program a new computer program. The three main limitations of the conventional group management data technique are addressed by this software, which is called the generalized structure of the group management data method (GSGMDH). By resolving the current issues, this program seeks to provide a straightforward and highly accurate model. In the GSGMDH, polynomials of degrees of two or three are conceivable. Furthermore, the inputs of the model are not limited to the layer next to it; that is, a neuron can receive two or three inputs at most. According to the description that was given, each virtual variable has one of the following classes as its structure:

1. A polynomial of the second order with two variables as inputs is represented by Eq. (21).

2. A polynomial of the second order with three variables as inputs is represented by Eq. (22).

3. A polynomial of the third order with two variables as inputs is represented by Eq. (23).

4. With three variables as inputs, the polynomial in Eq. (24) is of the third order.

$$ W_{kl = } a_{0} + a_{1} x_{k} + a_{2} x_{k}^{2} + a_{4} x_{l}^{2} + a_{5} x_{k} x_{l} k, \, l = 1, \ldots ,M $$
(21)
$$ w_{klq = } a_{0 + } a_{1} x_{k} + a_{2} x_{1} + a_{3} x_{q} + a_{4} x_{k}^{2} + a_{5} x_{l}^{2} + a_{6} x_{q}^{2} + a_{7} x_{k} x_{l} + a_{8} x_{k} x_{l} + a_{8} x_{k} x_{q} + a_{9} x_{l} x_{q} $$
(22)
$$ W_{kl} = a_{0} + a_{1} x_{k} + a_{2} x_{1} + a_{3} x_{k}^{2} + a_{4} x_{l}^{2} + a_{5} x_{k} x_{l} + a_{6} x_{k}^{3} + a_{7} x_{l}^{3} + a_{8} x_{k}^{2} x_{l} + a_{9} x_{k} $$
(23)
$$ \begin{aligned} W_{klq} = & a_{0} + a_{1} x_{k} + a_{2} x_{l} + a_{3} x_{q} + a_{4} x_{k}^{2} + a_{5} x_{l}^{2} + a_{6} x_{q}^{2} + a_{7} x_{k} x_{l} + a_{8} x_{k} x_{q} + a_{9} x_{l} x_{q} \\ & + a_{10} x_{k}^{3} + a_{11} x_{l}^{3} + a_{12} x_{q}^{3} + a_{13} x_{k}^{2} x_{l} + a_{14} x_{k}^{2} x_{q} + a_{15} x_{l}^{2} x_{k} + a_{16} x_{l}^{2} x_{q} \\ & + a_{17} x_{q}^{2} x_{k} + a_{18} x_{q}^{2} x_{l} + a_{19} x_{k} x_{l} x_{q} \\ \end{aligned} $$
(24)

In general, the GSGMDH is a robust and flexible technique and provides a set of equations in order to estimate the target function. The GSGMDH approach is quite more accurate than the classical GMDH method since this model can input from non-adjacent layers.

Outlier robust extreme learning machine (ORELM)

The concept for the extreme learning machine (ELM), a multilayer feedforward neural network, was developed by Huang et al. (2004, 2006). While the output weights are established analytically, the input weights are determined arbitrarily by ELM. The general layout of this method is shown in the diagram designated Fig. 2a. The primary distinction between an ELM and a single-layer feedforward neural network (SLFFNN) is that the latter does not apply any bias at all at the output neuron. It is feasible to create connections between each and every neuron in the hidden layer and the input layer. While the activation function of the neuron in the output layer is linear, it may take the shape of a piecewise continuous function within the hidden neurons. The utilization of many methods for weight and bias calculation by the ELM model results in a noteworthy decrease in the training duration of the network. This mathematical description can be applied to a single-layer feedforward neural network with n number of hidden nodes according to the following description:

$$ f_{n} (x) = \sum\limits_{i = 1}^{n} {\beta_{i} G(a_{i} ,b_{i} ,x)} $$
(25)

The weight between the ith hidden node and the output node is represented by the variable βi. The training factors for the hidden nodes are represented by the variables (ai) and bi. The output of the ith node, given the input x, is designated by the variable G(ai, bi, x). The activation function g(x) can be recast as follows at the additive hidden node G(ai, bi, x). This rule might take many different shapes.

$$ G(a_{i} ,b_{i} ,x) = g\left( {a_{i} \cdot x + b_{i} } \right) $$
(26)

Activation functions are used to ascertain the response output of neurons. In an ELM network with j hidden layer neurons, i input neuron, and k training instances, the activation of neurons in the hidden layer for each training example is calculated using the following equation:

$$ H_{jk} = g\left( {W_{ji} X_{ik} } \right) + B_{j} $$
(27)

where g(.) can be any continuous nonlinear activation function, Xik is the input neuron for the kth training sample, Hik is the activation matrix of the jth hidden layer neuron for the kth training example, and Wji is the weight of the ith input neuron and the jth hidden layer neuron, Bj is the bias of the jth hidden layer neuron. This matrix provides the activation of all the hidden layer neurons for the examples used in training. This matrix indicates that j stands for the column and k for the row. The matrix H is written as the hidden layer of the neural network’s output matrix. The weights between the neurons of the hidden and output layers are applied by using the least squares fitting for the target values in the train mode versus the outputs of the hidden layer neurons for each training example. The following is the equivalent mathematical expression for this fitting, which is as follows:

$$ H\beta = T $$
(28)
$$ \beta = \left( {\beta_{1} , \ldots ,\beta_{j} } \right)j \times 1 $$
(29)

Now let us look at this equation: Eq. (30): where T is the vector representing the target values for training samples, and β is the weight that denotes the association between the neurons of the hidden layer and the neurons of the output layer.

$$ T = \left( {T_{1} , \ldots T_{k} } \right)_{k \times 1} $$
(30)

Equation (31) eventually makes it possible to calculate weights:

$$ \beta = H^{\prime}T $$
(31)

where

$$ H\left( {\tilde{a},\tilde{b},\tilde{x}} \right) = \left[ {\begin{array}{*{20}c} {G(a_{1} ,b_{1} ,x_{1} )} & \ldots & {G(a_{L} ,b_{L} ,x_{L} )} \\ {G(a_{1} ,b_{1} ,x_{N} )} & \ldots & {G(a_{L} ,b_{L} ,x_{N} )} \\ \end{array} } \right]_{N \times L} $$
(32)
$$ \beta = \left[ {\begin{array}{*{20}c} {\beta_{1}^{T} } \\ : \\ {\beta_{L}^{T} } \\ \end{array} } \right]_{L \times m} \;{\text{and}}\;T = \left[ {\begin{array}{*{20}c} {T_{1}^{T} } \\ : \\ {T_{L}^{T} } \\ \end{array} } \right]_{L \times m} $$
(33)

here \(\tilde{a} = a_{1} , \ldots ,a_{L} ;\tilde{b} = b_{1} , \ldots ,b_{L} ;\tilde{x} = x_{1} , \ldots x_{L}\) and the weight vector between the neurons of the hidden layer and the input layer is denoted by the symbol β, and H′ represents the Moore–Penrose pseudo-inverse of the matrix H. The symbol T symbolizes the vector that refers to the vector that is between the training samples.

ELM training, based on the explanations, can be divided into two phases: the first involves randomly allocating weights and biases to the hidden layer neurons and computing the matrix H′s hidden layer output; the second phase computes the weight outputs by utilizing the Moore–Penrose pseudo-inverse of the matrix H and target values for various training samples. The hidden layer matrix (H) is found by a quick training process, which makes it faster than conventional iteration-based algorithms like Lundberg–Marquardt, which do not use a nonlinear optimization method. As a result, the time needed for network training is significantly decreased.

When employing artificial intelligence-based algorithms for modeling, outlier data is unavoidably present. This outlier data cannot be eliminated because the nature of the issue is often correlated with their occurrence. Consequently, it has a part that is a percentage of the total training error (e). Handling such data requires having sparsity as a distinguishing feature of the presence of outliers. Zhang and Luo (2015) are aware that using the l0-norm rather than the l2-norm can provide a sparser representation. An alternate method to using the l2-norm is to compute the output weight matrix (β) by treating the training error (e) in a sparse manner.

$$ \mathop {\min }\limits_{\beta } \,C\left\| {\mathbf{e}} \right\|\,_{0} + \left\| \beta \right\|_{2}^{2} \,\,\,\,\,\,{\text{subject}}\,{\text{to}}\,\,{\mathbf{y}} - {\mathbf{H}}\beta = {\mathbf{e}} $$
(34)
$$ \beta = [\beta_{1} ,...,\beta_{N} ]^{T} $$

(β) denotes the matrix of output weights (\({w}_{{\text{o}}}\) or the same \({w}_{{\text{output}}}\)):

$$ (\min_{w0} Ce_{0} + w_{02}^{2} \;\; subject\;to \;T - Hw_{0} $$

The equation that was just displayed is an illustration of a non-convex programming problem. Formulating this issue in the tractable convex relaxation form without removing the sparsity characteristic is one of the easiest ways to solve it. This is among the easiest approaches to handle this issue. The l1-norm is used to obtain the sparse term. In addition to producing a convex minimization, or a decrease in the error function, replacing l0-norm with l1-norm also guarantees the existence of limit events, or unusual data, or sparsity features.

$$ \mathop {\min }\limits_{\beta } \,\left\| {\mathbf{e}} \right\|\,_{1} + \frac{1}{C}\left\| \beta \right\|_{2}^{2} \,\,\,\,\,\,{\text{subject}}\,{\text{to}}\,\,{\mathbf{y}} - {\mathbf{H}}\beta = {\mathbf{e}} $$
(35)

To fully tune the proper domain of the augmented Lagrangian (AL) multiplier, the above-mentioned formula is a restricted convex problem.

$$ L_{\mu } ({\mathbf{e}},\beta ,\lambda ) = \left\| {\mathbf{e}} \right\|_{1} + \frac{1}{C}\left\| \beta \right\|_{2}^{2} + \lambda^{2} ({\mathbf{y}} - {\mathbf{H}}\beta - {\mathbf{e}}) + \frac{\mu }{2}\left\| {{\mathbf{y}} - {\mathbf{H}}\beta - {\mathbf{e}}} \right\|_{2}^{2} $$
(36)

The penalty parameter and the Lagrangian multiplier vector are represented by the symbol \(\mu = = 2N/\left\| {\mathbf{y}} \right\|_{1}\) in this context. Using the data from Yang and Zhang (2011), the following function is minimized iteratively to arrive at the best solution (e, β) and the Lagrangian multiplier vector (λ).

$$ \left\{ \begin{gathered} ({\mathbf{e}}_{k + 1} ,\beta_{k + 1} ) = \arg \,\,\mathop {\min }\limits_{e,\beta } L_{\mu } (e,\beta ,\lambda )\,\,\,\,\,\,\,\,\,\,\,\,(a) \hfill \\ \lambda_{k + 1} = \lambda_{k} + \mu ({\mathbf{y}} - {\mathbf{H}}\beta_{k + 1} - e_{k + 1} )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(b) \hfill \\ \end{gathered} \right\} $$
(37)

Self-adaptive extreme learning machine

The differential evolution algorithm can be used in the form of self-adaptiveness to get over current limitations, such as control parameters inside the algorithm and the choice of trial vector approach. Consequently, the self-adaptive extreme learning machine (SAELM) algorithm was introduced by Cao et al. (2012) to optimize hidden node biases and network input weights. To get the intended outcomes, this was done. The activation function g(K), L hidden nodes, and training data sets are required to develop the SAELM method.

The integration of the SAELM and ORELM models with the MOPSO optimization approach is the last stage of this inquiry that will successfully extract the rules of operation of dams in real time. The ideal release volume in real time is determined using four parameters: monthly inflows, the amount of water held in the reservoir the month before, fluctuations in reservoir capacity at the start of each month, and the downstream need in the current month. After the MOPSO algorithm has determined the ideal dam release parameters, this is carried out throughout the ensuing years. In the upcoming years, the MOPSO algorithm's outputs and deep learning approaches will be used to help with the operation. The process flowchart is located in Fig. 3, which is accessible at this link.

Fig. 3
figure 3

Combination of MOPSO algorithm with deep learning methods

Full size image

Results

Results acquired from optimization method

The MOPSO algorithm is run through a total of 1000 iterations while accounting for the 48 particles in order to optimize the system. Other parameters such as c1r1 and c2r2 coefficients were considered equal to 1.5 and 2, respectively, for better convergence of the algorithm. In the final iteration of the procedure, the set of optimal solutions is achieved. These solutions are shown between the goals \(F_{1}\) and \(F_{2}\) on the Pareto graph, which is also called the optimal exchange curve of goals (Fig. 4). The MOPSO algorithm uses the crowding distance function to select the best solutions for each iteration, much to the NSGA-II approach. Then, in order to move on to the next optimization stage, these solutions are saved under the Pareto front name. The points that are shown on the Pareto front are a collection of the twenty-four optimal solutions that the approach was able to extract. The axes of the Pareto graph reflect the objective functions \(F_{1}\) and \(F_{2}\).

Fig. 4
figure 4

Pareto graph (Pareto front) at the last optimization iteration

Full size image

The solution that has the most favorable value for both of the desired objective functions \(F_{1}\) and \(F_{2}\) is chosen as the optimal solution in contrast to alternative solutions based on the values of the objective functions, and answer 16 is thought to be the best appropriate response in this research because the Pareto graph showed that it exhibits this attribute. The best choice variables are incorporated into the WEAP model once solution number 16 is put into practice, and the system’s behavior is examined in light of this solution. Figure 5 shows the values of the percentage of meeting the requirements of each of the numerous uses after the system optimization is complete.

Fig. 5
figure 5

Coverage of demand sites following system improvement

Full size image

The results show that system optimization during the 360-month planning period results in better and more principled management of the reservoir during severe drought circumstances. Furthermore, for the entire duration, the needs are met in the best possible way. The application of water hedging policy with the aid of the optimization algorithm in arid and semi-arid regions not only achieves the desired and acceptable level of reliability, but also reduces the number of months of failure as well as the severity of failure during these months. This is especially helpful at those crucial times when we are facing a severe water deficit. In September and October, the average percentage of supply to demand has a minimal value of 81.1 and 81.4%, respectively. This is a decent statistic. Moreover, during the 360-month planning period, the ideal release values from the dam reservoir are determined once the system has been optimized. Therefore, we try to create a structure based on the output of the MOPSO method for the fresh data of the reservoir’s inflow by using the GSGMDH model. Real-time calculations are made to determine the ideal reservoir outflow values based on this structure. As was previously said, these figures may not be ideal for the sequence of upcoming inflows into the reservoir because they are derived from historical data on the inflow to the reservoir. In order to ensure the accuracy of the GSGMDH model, its performance is compared with that of the ORELM and SAELM models.

The outcomes of using the ORELM and SAELM models in comparison with the GSGMDH model

To take advantage of real-time optimization results, the GSGMDH model is used in this study and compared to the ORELM and SAELM models. The first 288 months of training are dedicated to training these models with the output of the MOPSO algorithm. After that, the data that was not used during the training phase is validated for a further 72 months. The amount of water pumped into the reservoir at the beginning of each month, the volume of water stored in the reservoir at the beginning of the month, changes in the reservoir’s storage, and the demands of downstream users are all taken into consideration when determining the ideal release amount for this duration of time based on these models.

The output of the optimization method is being compared with the outcomes during both the training and testing phases. Based on the inputs mentioned, the best artificial intelligence model needs to be able to predict the ideal dam release values, and its conclusions ought to differ as little as possible from the outcomes that the optimization algorithm has generated and attained. Table 2 presents the outcomes of these models’ predictions of the dam’s outflow based on the optimization algorithm’s findings. During the training and testing phases, these outcomes are contrasted with the output of the optimization technique.

Table 2 Prediction of optimal release volume from Ilam dam by different artificial intelligence models in tran and test stages
Full size table

The GSGMDH model is thought to be the most accurate model when compared to the ORELM and SAELM models in the two training and testing phases since it has the lowest values of the RMSE and NRMSE evaluation indices and the greatest values of the NASH and R indices overall. Table illustrates this (2).

Figure 6 illustrates how well the GSGMDH model’s trained structure predicts the ideal dam release in a range of months for both the train and test stages. This graphic also shows the relative error rate of the built model in terms of figuring out the optimal amount of discharge from the dam based on fresh data.

Fig. 6
figure 6

Predicted values of the outflow by the GSGMDH model in the train and test phases compared to the output of the MOPSO algorithm

Full size image

Figure 7 shows the value of the correlation coefficient between the data predicted by GSGMDH and the output data of the MOPSO algorithm during the two training and testing phases. It is also discussed how these spots are distributed around the y = x line. This figure’s high R value indicates that the support vector machine model does a good job of predicting the dam’s ideal output given the current time.

Fig. 7
figure 7

The distribution of the output points of the MOPSO algorithm and predicted by the GSGMDH model around the y = x line in the train and test phases

Full size image

Conclusions

The results showed that the model built by connecting the WEAP simulation model with the MOPSO multi-objective algorithm has the proper capacity and efficiency to tackle challenging, fully nonlinear problems and to yield optimal solutions. The outcomes provided evidence of this. In the last algorithm iteration, 24 distinct solutions that fell inside the optimal Pareto front value were used to build the goal exchange curve. The optimal solution among these possibilities was determined to be the one with the lowest value of the objective functions. The assessment of the relevant objective functions served as the basis for this conclusion. The application of the optimal release values from the dam, when the optimal policy is taken into account, produced findings that demonstrate that the percentage of meeting the needs of most users is appropriate and acceptable, and that it is more than 90% in most months. The optimal release values or the optimal rule curve were produced as a result of using the MOPSO algorithm on a specific sequence of inflows to the reservoir throughout the operating time. In addition, given these circumstances, the reservoir's discharge was tailored to support downstream usage. The issue with these models is that the best answers are not transferable to other potential inflows into the reservoir in the upcoming years. It is possible that the found optimal solutions will not hold true when the inflow to the reservoirs varies, and an optimizer method should be used to optimize the system once more. This is the issue with these kinds of models. After that, in order to benefit from the real-time optimization results, the GSGMDH model was used instead of the ORELM and SAELM models. The results indicated that the GSGMDH model performed the best when compared to the ORELM and SAELM models. The RMSE, NRMSE, NASH, and R evaluation indices were used to calculate this; their respective values during the test stage were 1.08, 0.088, 0.969, and 0.972. The results showed that in the superior GSGMDH model, about 90% of the predictions had errors of less than 4%. While in other models (ORELM and SAELM) about 60% of noses had this amount of error. It is therefore offered as the best model for figuring out the largest dam rule curve pattern in real time. The structure that was created as a result of this research can be used to identify the ideal release quantity in real time. This structure accounts for the monthly inflow into the reservoir, the reservoir's initial water storage volume, variations in the reservoir’s storage, and the demands of users downstream during the course of the current month. To put it another way, the GSGMDH model that was developed possesses the ability to quickly provide optimal operating policies in line with the new dam inflows in a way that permits optimal system management at all times. It is suggested to use the model developed in this research to plan and manage the operation of dam and aquifer systems for the coming years. It is suggested to use artificial intelligence models that have multiple output layers in multi-dam systems where each dam has a separate command curve, but the release of each of these dams is affected by each other. These models can be developed in the MATLAB environment for new conditions. Also, part of the information needed for such models can be obtained from online databases that are received from different satellites. This is especially important in areas without statistics.