Safety’s coordination problems

Abstract

The safety conception of knowledge holds that a belief constitutes knowledge iff relevantly similar beliefs—its epistemic counterparts—are true. It promises an instructive account of why certain general principles of knowledge hold. We focus on two such principles that anyone should endorse: the closure principle that knowledge is downward closed under competent conjunction elimination, and the counter-closure principle that knowledge is upward closed under competent conjunction introduction. We argue that anyone endorsing the former must also endorse the latter on pains of an unacceptable form of bootstrapping. We devise new formal models to identify necessary and sufficient conditions for these principles to hold on conceptions that construe knowledge in terms of true counterparts. These conditions state that counterparts of premise and conclusion beliefs are coordinated in certain ways whenever these beliefs stand in the relevant inferential relations. We show that the safety conception faces insuperable problems vindicating these coordination principles, because its epistemic counterpart relation is symmetric. We conclude that it thus proves unable to account for minimal closure properties of knowledge. More generally, our formal results establish parameters within which any conception must operate that construes knowledge in terms of true counterparts.

1 Introduction

A belief is safe iff all beliefs similar to it are true (see Williamson 2009a). Whether a belief is similar to another depends on a confluence of factors, including their respective subject matter (or topic), the circumstances in which they are formed or sustained, and the means by which they are arrived at. Radically different topics, radically different circumstances, and radically different means, each make for dissimilarity among beliefs. It is far from clear, however, whether there is any reductive account of the similarity among beliefs in terms of the similarities exemplified by a finite number of such factors and their interaction.

Many consider safe belief, thus understood, as a good explication of knowledge, even if they agree that it doesn’t furnish us with any analysis, or real definition, of knowledge. Call this the safety conception of knowledge.¹

In many respects, the safety conception of knowledge proves very powerful—for instance, when it comes to Gettier cases and scepticism (Williamson, 2000, 2009a). But it also promises an instructive account of what we might call ‘the structure of knowledge’, providing insights into why certain general principles of knowledge hold and others do not. For, instead of merely rephrasing such principles in terms of safe belief rather than knowledge, and insisting that, recast in this way, these principles do or do not hold, the safety conception promises to explain why this is so by exploiting features of similarity and its interaction with other notions such as competent deduction, entailment, and the like.

Here we shall argue that modelling knowledge on safe belief nonetheless faces unexpected difficulties in the latter regard. More specifically, we shall argue, first, that, once it validates an eminently plausible, and rather limited, principle of closure for knowledge, it must likewise validate an equally plausible and limited principle of counter-closure. We then proceed to show that the safety conception is incapable of, and in fact inimical to, successful completion of the latter task. This, in turn, casts doubt on its ability to validate the closure principle in question.

To avoid cumbersome formulations, it will be handy to have a noun phrase to refer to the beliefs that are similar to a given belief. We will call them its epistemic counterparts, or counterparts for short. Thus, a belief is safe iff it only has true counterparts. In the context of our discussion of the safety conception of knowledge, we will correspondingly sometimes use “counterpart relation” for “similarity”. Familiar versions of safety correspond to different notions of similarity. On a simple version, one’s belief that p is safe iff in any close case in which one believes that p, it is true that p (Williamson, 2000, 126–127). On that version, two beliefs are similar iff they have the same content and are held in close cases. On another version, one’s belief that p is safe iff in any close case in which one believes a proposition p* close to p, on a basis b* close to the actual basis b of one’s belief, it is true that p* (Williamson 2009a, 325). On that version, two beliefs are similar iff they have close contents, and are held on a close basis in a close case. Recasting talk of similarity in terms of talk of counterparthood allows us to abstract away from details and focus on structural features common to all variants of safety.

The safety conception is committed to the symmetry of its (epistemic) counterpart relation because similarity is a symmetric relation. As we shall see, at crucial junctures, the problems we diagnose for the safety conception of knowledge arise from this commitment. Our arguments thus leave open whether there is a viable framework that retains the idea that a belief’s being knowledge is to be understood to consist in the truth of all its counterparts, but that construes the counterpart relation as some alternative, non-symmetric relation—say, one of comparative normality (Beddor & Pavese, 2020; Carter, 2019; Carter & Goldstein, 2021; Dutant, 2016; Goodman & Salow, 2018, 2023; Greco, 2014; Loets, 2022; Stalnaker, 2015).

Consider sceptical scenarios, for instance. In the good case, one’s circumstances are normal and one knows that one has hands. In the bad case, one undergoes similar experiences and inner processes, and believes that one has hands, but one doesn’t have hands, and so doesn’t know that one has hands. If knowledge requires that all the counterparts of one’s belief are true, then we must say that one’s belief in the bad case is not a counterpart of one’s belief in the good case. Safety theorists say that it is too dissimilar: the two beliefs are held in different circumstances, or they involve different bases (where a belief’s basis includes its relation to one’s environment). However, by the same token, the good case belief is not then a counterpart of the bad case belief. Contrast this with a bare-bones normality-based conception on which the counterparts of a belief are beliefs that are at least as normal as that belief (where normality is a matter of how normal the circumstances and bases of these beliefs are, in some suitable sense of normality, likewise understood in a non-reductive spirit; note that we need not assume that normality is a total order: perhaps some pairs of beliefs are incomparable). The bad case belief is less normal than the good case belief because its circumstances are less normal. Therefore, the former is not a counterpart of the latter, but the latter is a counterpart of the former: counterparthood is not symmetric.

The problems the safety conception faces when it comes to validating plausible closure and counter-closure principles arise from the symmetry of its counterpart relation. These problems do not beset alternative conceptions of counterparthood that reject symmetry. That alone does not guarantee, though, that these alternative conceptions do validate the principles in question. The formal results we establish below delineate constraints that such alternative conceptions must satisfy to validate various closure and counter-closure principles.

2 Bootstrapping, closure under conjunction elimination, and counter-closure under conjunction introduction

While drawing deductive inferences is often a way to extend one’s knowledge, here’s one way it which it cannot do so. Suppose p is something you believe but fail to know. Combining p with an unrelated proposition q that you also believe, you competently deduce, and thereby come to believe, the conjunction p∧q. From your belief in the conjunction, you proceed to competently deduce p, again coming to believe p. Clearly, this is no way to bootstrap your initial belief into knowledge.²

We say that q is an “unrelated” proposition. For, there may well be cases in which one believes but fails to know p, conjoins p with some q one also believes, deduces p again and thereby comes to know p. This may happen, for instance, if q is something one knows that obviously entails p or serves as an inductive basis on which one can come to know p, but where this relation to p had eluded one before. Setting such cases aside, however, the following constraint seems to us non-negotiable:

• NO BOOTSTRAPPING. If one believes each of p and q, and one believes p∧q solely based on competent conjunction introduction from these beliefs, and one believes p again based on competent conjunction elimination from the conjunctive belief, then one’s deduced belief in p constitutes knowledge only if one’s initial belief in p did.

For instance, suppose you believe, on the basis of casual perception, both that the building in front of you is a barn and that it has a door, and you then competently deduce, and come to believe, that the building in front of you is a barn with a door, where this conjunctive belief is based on nothing else. Suppose further you proceed to competently deduce, and thereby come to believe again, that the building in front of you is a barn. Then, the latter belief will be knowledge only if your initial belief to the same effect already was. Thus, if you are in barn façade county and you cannot come to know, based on casual perception alone, that the building in front of you is a barn, then you can’t bootstrap your belief that it is into knowledge by the envisaged sequence of inferential steps either.

It is widely disputed whether, in general, knowledge is closed under competent deduction (Nozick, 1981; Dretske, 1970, 1971 and 2005; Kripke, 2011; Holliday 2013; Yablo, 2014; Berto, 2022; for a defence, see Hawthorne, 2005). However, most epistemologists are happy to endorse the idea that knowledge is closed under competent conjunction elimination:

• CE-CLOSURE. If one believes p based on competent conjunction elimination from some conjunction p∧q that one also believes, then, if the latter belief constitutes knowledge, so does the former (Williamson, 2000).

Thus, if you do know that the building in front of you is a barn with a door, and competently deduce by conjunction elimination, and thereby come to believe, that the building in front of you has a door, then the latter belief will likewise constitute knowledge.

Many who are critical of the general principle of closure nonetheless accept that, if one knows p∧q, one thereby already knows each of p and q. No deductive inference is needed to get from the former to the latter: knowing p∧q already is a way of knowing each of p and q (Berto, 2022; Williamson, 2000; Yablo, 2014). This is sometimes called ‘immanent closure’ (Berto, 2022; Yablo, 2014). Friends of immanent closure should find no fault with CE-CLOSURE, even if knowledge is not, in general, closed under competent deduction.³

Let’s accordingly assume that CE-CLOSURE is a valid principle of knowledge.⁴ But now, note that, in conjunction with the NO-BOOTSTRAPPING CONSTRAINT, CE-CLOSURE implies that if you believe but do not know p, and you combine that belief with another belief in some q to competently deduce the conjunction p∧q, you cannot thereby come to know p∧q. For, if you could, by CE-CLOSURE, knowledge of p would be only one simple competent deductive step away—in evident violation of the NO-BOOTSTRAPPING CONSTRAINT.⁵

Accordingly, setting aside special cases of the sort previously identified, CE-CLOSURE and the NO-BOOTSTRAPPING CONSTRAINT force acceptance of the following principle:

• CI-COUNTER-CLOSURE: If one believes p∧q solely based on competent conjunction introduction from some p and q each of which one also believes, then, if the former belief constitutes knowledge, so do the latter.

CI-COUNTER-CLOSURE contrasts with the general principle of counter-closure according to which any knowledge solely acquired by competent deduction from a set of believed premises requires that the premise beliefs in question be knowledge, too. The latter principle is highly controversial, as it seems that, in certain cases, one might arrive at knowledge by deduction from false premises. There are those who take these cases at face value and reject the general principle of counter-closure on these grounds (Warfield, 2005; Luzzi, 2010; Hawthorne and Rabinowitz 2017; Fitelson 2017; Almeida 2017). And then there are those who uphold that principle and argue that, appearances notwithstanding, these are cases in which the conclusion belief is not, or at least not solely, based on the false premise beliefs (Klein, 2008; Ball & Blome-Tillmann, 2014; Montminy, 2014; Schnee, 2015, Borges 2017).

No matter what stance one takes on this issue, the disputed cases all involve weakening, i.e., a deductive inference in which the conclusion is logically weaker than the conjunction of the premises (see, e.g., the list of cases in Hawthorne and Rabinowitz 2017: 330–31). CI-COUNTER-CLOSURE, by contrast, exclusively concerns instances of competent conjunction introduction where the conclusion is exactly as strong as the conjunction of the premises. We know of no comparable challenges to the idea that knowledge is counter-closed under competent conjunction introduction. Thus, pending further argument, even opponents of the general principle of counter-closure may accept it.

In any case, we just saw that, in the light of the NO-BOOTSTRAPPING CONSTRAINT and setting aside certain special cases, CE-CLOSURE—i.e., the principle that knowledge is closed under competent conjunction elimination—forces acceptance of CI-COUNTER-CLOSURE. Accordingly, to the extent that both the NO-BOOTSTRAPPING CONSTRAINT and CE-CLOSURE seem eminently plausible, opposition to CI-COUNTER-CLOSURE is hard to sustain.⁶

We go on to show that, somewhat surprisingly, proponents of the safety conception of knowledge have a hard time validating CI-COUNTER-CLOSURE. If so, this will cast doubt on their ability to validate CE-CLOSURE, as the NO-BOOTSTRAPPING CONSTRAINT seems non-negotiable. To this end, we will first devise a logical framework and prove two important correspondence results, identifying non-trivial conditions that are both necessary and sufficient for the safety conception of knowledge to validate closure and counter-closure under various deduction relations.

3 Doxastic counterpart frames

To motivate our logical framework, consider first how the safety conception validates the principle of factivity for knowledge. It does not do so by simply insisting that, if a given belief has only true counterparts, that belief is itself true. Rather, it does so by construing the counterpart relation as reflexive: since every belief is similar to itself, it is a counterpart of itself; accordingly, if all its counterparts are true, so is that belief.

To recover that result formally, we need to consider the counterpart relation in abstraction from the specific truth conditions assigned to beliefs. For, if we did not, we would encounter models in which factivity holds, as it were, ‘by accident’. For instance, consider models where the counterpart relation is not reflexive but every belief that is not a counterpart of itself happens to be a belief in a tautology. Such models are obviously gerrymandered ways of satisfying factivity. To screen them off, we need to look at counterparthood frames that abstract away from the truth conditions of beliefs. In such frames, the reflexivity of the counterpart relation is both necessary and sufficient for factivity.

Formally, let a BC frame consist of a non-empty set of cases (or centred worlds), a non-empty set B of token beliefs, with each token belief belonging to exactly one world, and a counterpart relation C between these token beliefs. A BC model supplements a BC frame with an assignment function, A, that associates each token belief in B with a truth condition: a set of worlds in which the belief’s content is true.⁷ A token belief is true in a BC model iff its world belongs to its assigned truth set, and it is safe in a BC model iff all its counterparts are true in that model.

While some models with a non-reflexive counterpart relation can nonetheless validate factivity for safe belief, i.e., the principle that every safe belief is true, reflexivity of the counterpart relation is both necessary and sufficient for a BC frame to validate factivity. For, suppose that the counterpart relation in such a frame is not reflexive. Then, for some belief α of some model, the assignment function A may assign the universal set to each of α’s counterparts and the empty set to α. Hence, α is safe in the model but false. Consequently, as is familiar from standard modal logic, distinguishing frames from specific models allows us to establish a meaningful correspondence result linking factivity and reflexivity.⁸

Let us now consider extending BC frames by adding two relations, E and D, between individual beliefs or sets of beliefs and individual beliefs. Here, E is meant to stand for a relation of entailment between individual beliefs, or collections thereof, and individual beliefs, with the latter’s truth-set including (the intersection of) the former’s truth-set(s).

The relation D is meant to stand for an arbitrary deductive relation, but we leave its specific interpretation open. It is restricted to hold exclusively among co-worldly (or, as we sometimes put it, co-existing) token beliefs—a belief is only ever inferred from beliefs held in the same case—and requires premise beliefs to jointly entail the conclusion belief.

It might be desirable to further assume that D is irreflexive (no belief is deduced from itself) and satisfies a cut property: if a conclusion belief is deduced from premise beliefs that are themselves deduced from further premise beliefs, the conclusion belief is deduced from these further premise beliefs, too. The results we establish here still hold if these further constraints are imposed.

The frames then allow us to ask what is necessary and sufficient for safe belief to be closed, or counter-closed, under the D-relation in question. As shown in the Appendix, two correspondence results hold. Using “deduce” for an arbitrary deduction relation:

• Closure under deduction holds in all and only downward coordinated frames, where a frame is downward coordinated iff the following condition holds: if belief α is deduced from premise beliefs Γ, then any counterpart of α is jointly entailed by some co-worldly counterpart(s) of some premise belief(s) in Γ.

• Counter-closure under deduction holds in all and only upward coordinated frames, where a frame is upward coordinated iff the following condition holds: if belief α is deduced from premise beliefs Γ, then then any counterpart of a belief in Γ is jointly entailed by some co-worldly counterpart(s) of α.

To see why, on the safety conception of knowledge, downward coordination suffices for the validity of closure, suppose that belief α is deduced from premise beliefs Γ and that α is not safe and hence has false counterparts. Given downward coordination, if there is a false counterpart α′ of α, α′ will jointly be entailed by some counterparts of some beliefs in Γ. But then, one of these counterparts must be false, whence it follows that not all premise beliefs in Γ are safe. Conversely, if all premise beliefs are safe, then so is the conclusion belief.

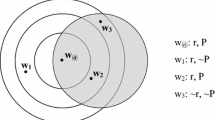
To see why downward coordination is necessary for the validity of closure, suppose that a frame is not downward coordinated: for some belief α deduced from premise beliefs Γ, and some counterpart α′ of α, no sets of counterparts of beliefs in Γ co-worldly with α′ entail α′ (see Fig. 1). Consider the model based on that frame which assigns the universal set to any belief jointly entailed by some co-worldly counterparts of some beliefs in Γ, and the empty set to any other belief. Because entailment is reflexive, this ensures that the premise beliefs Γ are safe in the model, but also that α′ is false in the model, in which event closure fails.

Fig. 1

Downward and upward coordination. Dots stand for single token beliefs, circles for sets of token beliefs, thin arrows for counterparthood, thick solid arrows for deduction and thick double arrows for entailment. Coordination conditions are violated on the left and satisfied on the right. For instance, in the top left graph, the conclusion belief has a solitary counterpart in w₂ that fails to be entailed by co-worldly counterparts of the premise beliefs

To see why, on the safety conception of knowledge, upward coordination suffices for the validity of counter-closure, suppose that belief α is deduced from premise beliefs Γ and that α is safe so that all its counterparts are true. Since, by upward coordination, any counterpart of any premise belief in Γ is jointly entailed by co-worldly counterparts of α, all counterparts of any premise belief in Γ are true, so the beliefs in Γ are safe.

To see why upward coordination is necessary for counter-closure, suppose that a frame is not upward coordinated: for some belief α is deduced from premise beliefs Γ and for some counterpart β of some belief in Γ, β is not jointly entailed by any co-worldly set of counterparts of α (see again Fig. 1). Consider the model based on that frame that assigns the universal set to any belief jointly entailed by any co-worldly set of counterparts of α, and the empty set to any other belief. Because entailment is reflexive, this ensures that all counterparts of α are true, but also that β is false, in which event some premise belief in Γ is not safe.

Interpreting D now as the relation of being arrived at by competent conjunction elimination, it follows that CE-CLOSURE is valid on a BCDE frame iff the following holds:

• CE-DOWNWARD COORDINATION. If belief α is arrived at by competent conjunction elimination from belief β, then any counterpart of α is entailed by some co-worldly counterpart of β.

Interpreting D as the relation of being solely arrived at by competent conjunction introduction, CI-COUNTER-CLOSURE is valid on a BCDE frame iff the following holds:

• CI-UPWARD COORDINATION. If belief α is solely arrived at by competent conjunction introduction from beliefs Γ, then any counterpart of a belief in Γ is entailed by some co-worldly counterpart of α.

CE-DOWNWARD COORDINATION and CI-UPWARD COORDINATION are thus necessary and sufficient for the safety conception of knowledge to deliver CE-CLOSURE and CI-COUNTER-CLOSURE, respectively, solely based on features of the counterpart relation and its interaction with the entailment relation and the deduction relation relevant in each instance. This is the kind of instructive, non-trivial account of the validity of those principles that we were primed to expect.

Let us illustrate both constraints in more familiar terms. Say that the counterparts of a belief are beliefs based on the same method as that belief, held in close cases. A sufficient condition for downward coordination is:

• EXTENDED METHODS. If one believes a conclusion by competent deduction from some premises, one’s method for believing the conclusion is to deduce a belief from beliefs based on one’s methods for believing the premises.⁹

For, suppose a belief is a counterpart of one’s conclusion belief. Then it is located at a close case and deduced from co-worldly beliefs based on the same methods one uses to believe the premises. These beliefs are, therefore, counterparts of one’s premise beliefs and entail the counterpart of the conclusion belief. Hence downward coordination holds. As several authors have noted, EXTENDED METHODS is sufficient for closure under competent deduction (Williamson 2009b, 326; Das & Salow, 2018; Schulz, 2020; Luper, 2020; Hawthorne & Goldstein 2024). Our result shows that EXTENDED METHODS is in fact stronger than necessary: counterparts of the conclusion belief only need to be entailed by some counterparts of the premise beliefs.

EXTENDED METHODS is not sufficient for upward coordination, however, and plausibly incompatible with it. To see the tension, imagine that one deduces $p\vee q$ from a belief in p that is itself acquired by a non-deductive method and suppose further that one does not deduce anything else from any belief acquired by that non-deductive method. By EXTENDED METHODS, the conclusion belief has no co-worldly counterparts but itself. But it does not entail the premise belief. Therefore, the premise belief has a counterpart, namely itself, that is not jointly entailed by any co-worldly counterparts of the conclusion belief: upward coordination fails. This result need not trouble a safety theorist who endorses EXTENDED METHODS, for they may already think that counter-closure under deduction in general fails, notably when one deduces a conclusion that is weaker than one’s premises. But, CI-COUNTER-CLOSURE remains eminently plausible. Can safety theorists validate it?

4 Inheritance and contagion

So, given the way we have framed matters, safety theorists need CI-UPWARD COORDINATION to validate CI-COUNTER-CLOSURE. However, at first sight, CI-UPWARD COORDINATION seems implausible. Sometimes one draws an inference but could easily have failed to do so. There then is a close case where, all else being equal, one has premise beliefs of the same type, but doesn’t form any corresponding conclusion belief. It is natural to think that the premise beliefs in this close case are relevantly similar, and hence counterparts, of the premise beliefs in the original case. But since, in that close case, no corresponding conclusion is drawn, there then seems to be no counterpart of the original conclusion belief, in violation of CI-UPWARD COORDINATION. Call such a close case a ‘missing conclusion case’.

However, note that all that CI-UPWARD COORDINATION requires is that, wherever there are counterparts of the premise beliefs, there are some co-worldly counterparts of the conclusion belief entailing them. Even in scenarios with missing conclusion cases, though, there are beliefs that jointly entail the counterparts of the premise beliefs, viz. those counterparts of the premise beliefs themselves. This suggests that CI-UPWARD COORDINATION could be ensured by a principle according to which a belief arrived at solely by competent conjunction introduction inherits the counterparts of its premise beliefs:

• INHERITANCE. If belief α is solely arrived at by competent conjunction introduction from beliefs Γ, then any counterpart of a belief in Γ is itself a counterpart of α.

Given that entailment is reflexive, it is easy to see that INHERITANCE entails CI-UPWARD COORDINATION.

One initial reaction to this proposal is that INHERITANCE stretches the notion of similarity beyond plausibility. For, while the original conclusion belief is based on a deductive inference, in scenarios with missing conclusion cases, the counterparts of its premise beliefs may, like those premise beliefs themselves, be based on perception instead. Equally, however, like the original premise beliefs and their counterparts, the original conclusion belief, too, may be said to rely on, and so to ultimately be based on, the methods on which the former are based. So, perhaps, the friend of the safety conception of knowledge may after all still make sense of the idea that the original conclusion belief is relevantly similar to the counterparts of its premise beliefs in scenarios with missing conclusion cases.¹⁰

We can recast the point in more familiar terms, assuming that counterparts of a beliefs are beliefs based on the same method at close cases. If one deduces a conclusion by competent conjunction introduction from some premises but could easily have failed to do so, there is a missing conclusion case in which one still believes the premises but fails to form a belief in the conclusion. The case is close, and presumably one’s methods for believing the premises are the same, so these are counterparts of the premise beliefs (being used as premises for an inference is not an essential part of the methods on which they are based). But, there does not seem to be a counterpart of the conclusion belief in that case. Indeed, that there is no such counterpart follows from EXTENDED METHODS, if, as we are free to stipulate, the premise beliefs were non-deductive and in the close missing conclusion case no belief at all is deduced from any beliefs based on these methods. Hence, CI-UPWARD COORDINATION fails. However, in response, one might suggest replacing EXTENDED METHODS by:

• INHERITED METHODS. If one believes a conclusion by competent conjunction introduction from some premises, one’s method for believing the conclusion is to either deduce a belief from beliefs based on one’s methods for believing the premises or base a belief on one of one’s methods for believing the premises.

At first sight, this stretches the notion of being based on the same method beyond plausibility. One of the premise beliefs may be based on simple perception, while the conclusion belief may involve conjoining the former with beliefs deriving from very different sources.¹¹ However, the conclusion belief does rely on what the premise beliefs rely on, so perhaps one can make sense of the coarser notion of method involved in INHERITED METHODS. From this INHERITANCE follows, for the conclusion belief is based on the same method as any of the premise beliefs, and therefore any counterpart of the premise beliefs, i.e. any belief held at a close case on the basis of a method for believing one of the premises, is thereby a counterpart of the conclusion belief.

Sadly, however, friends of the safety conception of knowledge cannot endorse INHERITANCE without facing a devastating contagion problem.

For, suppose you know that the building in front of you has a door, falsely believe that it is a barn, and come to believe, falsely and solely based on competent conjunction introduction from those two beliefs, that the building in front of you is a barn with a door. By INHERITANCE, your true premise belief that the building in front of you has a door is a counterpart of your false conclusion belief that it is a barn with a door. That is, INHERITANCE counts your premise belief that the building in front of you has a door as being similar to your false conclusion belief that it is a barn with a door. But crucially, similarity is symmetric. This means that your premise belief, that the building in front of you has a door, has as one of its counterparts the false conclusion belief that it is a barn with a door. So, that premise belief isn’t safe. Modulo the safety conception of knowledge, this contradicts the assumption you know that the building in front of you has a door (see Fig. 2).

Fig. 2

The contagion problem for INHERITANCE. T and F indicate the truth-value of each belief. Counterpart arrows are labelled i if required by INHERITANCE and s if required by symmetry. If the conclusion belief is false, every premise belief has a false counterpart

Generalising, INHERITANCE entails that it is impossible for one to know a premise and competently deduce a false conclusion from it and other premises by simple conjunction introduction. But that is obviously possible.

The contagion problem for INHERITANCE crucially relies on the symmetry of the counterpart relation. However, similarity is, by its very nature, a symmetric relation. If friends of the safety conception of knowledge were now to replace similarity by some other, non-symmetric counterpart relation in their preferred account of knowledge, they would no longer profess a safety conception of knowledge.

Accordingly, friends of the safety conception of knowledge must reject INHERITANCE. Without INHERITANCE, however, there would seem to be no guarantee that the condition formulated by the principle of CI-UPWARD COORDINATION can always be met. But this is precisely the condition that would seem both necessary and sufficient for the validity of CI-COUNTER-CLOSURE. The latter principle is forced upon us by the NO-BOOTSTRAPPING CONSTRAINT in conjunction with CE-CLOSURE, neither of which it is remotely plausible to reject.

5 Upward coordination by proxy and revenge contagion

At this stage, the reader may complain that we have simply ignored the most natural diagnosis of scenarios with missing conclusion cases. Suppose you are in barn façade county, looking at a real barn with a door, and, by casual observation, form both the true belief that the building is a barn and the true belief that it has a door. Suppose you then arrive, solely based on competent conjunction introduction, at the true belief that the building is a barn with a door. Formed by casual observation in barn façade county, your premise belief that the building is a barn does not constitute knowledge, as you would similarly believe, by casual observation, of a barn façade, that it is a barn. It may not be that in all such unfortunate cases you also believe that the building has a door and deduce that it is a barn with a door. But this misses the point. For, there will nonetheless be similar cases in which you do: a case where you are looking at a barn façade and falsely believe it is a barn and, as in the original case, additionally form the belief that it has a door and arrive at the conjunctive belief that it is a barn with a door, solely based on competent conjunction introduction from those two premise beliefs. The resulting conclusion belief is both false and similar enough to the original true conclusion belief to ensure that the latter does not constitute knowledge—just as CI-COUNTER-CLOSURE demands.

The general idea underlying this diagnosis is that even if we cannot assume that there is a co-worldly counterpart of the original conclusion belief for every counterpart of its premise beliefs, it would be enough if, for any missing conclusion case in which there is a counterpart of a premise belief, there could be a further case in which there both is another such counterpart with the same truth-value as the first and also a counterpart of the other premise belief and in which one arrives at a conclusion belief by, and solely by, competent conjunction introduction from those two premise beliefs. The latter conclusion belief would be a counterpart of the original conclusion belief.

We call this assumption.

• PROXY CI-UPWARD COORDINATION. If belief α is solely arrived at by competent conjunction introduction from a belief β and other beliefs Γ, then, for any counterpart β′ of β, there is another counterpart β″ of β, with the same truth-value as β′, that co-exists both with counterparts Γ’ of the beliefs in Γ and a counterpart α′ of α such that α′ entails both β″ and the beliefs in Γ’.

Here, the counterpart β″ of β witnesses the fact that one could easily have drawn a competent conjunction introduction inference from β′ together with counterparts of the beliefs in Γ and reached a conclusion belief that would then be similar to the original conclusion belief (see Fig. 3).

Fig. 3

PROXY CI-UPWARD COORDINATION. Although the true “barn” premise belief has a solitary false counterpart at w₂ with no co-worldly counterpart of the “barn and door” conclusion belief—in violation of CI-UPWARD COORDINATION—it has another false counterpart at w₃, going proxy for the one in w₂ (as indicated by the dotted line), that is entailed by a co-worldly counterpart of the conclusion belief, ensuring that the original conclusion belief is not safe

An attractive feature of PROXY CI-UPWARD COORDINATION is that, unlike CI-UPWARD COORDINATION, it is compatible with EXTENDED METHODS. Assume that counterparts of a belief are beliefs based on the same method and held at close cases, and that EXTENDED METHODS holds. Suppose one forms a belief by competent conjunction introduction from some premises beliefs, including a belief that p. Suppose that at some close case, one has a belief that p* based on one’s method for believing that p, hence a counterpart of one’s belief that p. PROXY CI-UPWARD COORDINATION can be satisfied by there being another close case in which one not only has a belief that p** based on one’s method believing that p, with the same truth-value as one’s belief that p* in the second case, but also beliefs based on one’s methods for the other premise beliefs, and in which one deduces their conjunction. By EXTENDED METHODS, one’s belief in that conjunction is a counterpart of one’s conclusion belief, ensuring PROXY CI-UPWARD COORDINATION.

While PROXY CI-UPWARD COORDINATION is weaker than CI-UPWARD COORDINATION, it is nonetheless sufficient for CI-COUNTER-CLOSURE. For, suppose that some premise belief β has a false counterpart β′, then, by PROXY CI-UPWARD COORDINATION, there would be an equally false counterpart β″ of β entailed by some counterpart α′ of α. Since β″ is false, that counterpart of α would be false, too, and so, α would not be safe.

One might wonder how PROXY CI-UPWARD COORDINATION might be deemed sufficient for CI-COUNTER-CLOSURE, given our previous result that full-blown CI-UPWARD COORDINATION is necessary for it. In response, note that PROXY CI-UPWARD COORDINATION appeals to a further notion beyond counterparthood, competent conjunction introduction, and entailment, viz. the notion of two counterparts having the same truth-value. Since this notion is not formally represented in BCDE frames, the condition was not available as a condition for CI-COUNTER-CLOSURE. So, its sufficiency does not undermine our previous results that, if CI-COUNTER-CLOSURE is to follow from features of counterparthood, in relation to entailment and competent conjunction introduction alone, full-blown CI-UPWARD COORDINATION is both necessary and sufficient for CI-COUNTER-CLOSURE.

PROXY CI-UPWARD COORDINATION still is too strong a modal assumption, however. For, it may be that false counterparts of one premise belief simply cannot co-exist with counterparts of the respective other. This kind of constellation is exemplified by Kripke’s famous red barn example (Kripke, 2011: 186–91; cf. also Schaffer, 2001). Here is a more realistic example to illustrate the issue at hand:

Necessarily, a cookie with a message in it is a fortune cookie.¹² Kim has heard of fortune cookies but harbours some mistaken beliefs about what they are: they think a fortune cookie is any cookie served at the end of a meal. So, when presented with a cookie at the end of a meal, they believe but fail to know that it’s a fortune cookie. As they eat it, they realize it contains a piece of paper and notice that the paper has a message on it. So, they come to believe, and know, that this cookie contains a message. From these two beliefs, they competently deduce by conjunction introduction, and come to believe on that basis alone, that this cookie both is a fortune cookie and contains a message. This conjunctive belief does not constitute knowledge. Yet, in whatever way Kim might form false beliefs similar to their actual belief that the cookie is a fortune cookie—when they mistake some other type of biscuit for a fortune cookie, say—they could not do so while forming any belief similar to their actual belief that the cookie at hand contains a message—for any such belief would be formed by chewing on a piece of paper found in a cookie, and the cookie in question would then have to be a fortune cookie. Accordingly, PROXY CI-UPWARD COORDINATION will be violated.

Fortunately, upon reflection, PROXY CI-UPWARD COORDINATION is not strictly necessary for CI-COUNTER-CLOSURE. While, for any false counterpart of one of the premise beliefs, the safety theorist needs a false counterpart of the conclusion belief, they do not need the latter to be inferred from counterparts of all the original premise beliefs. In the fortune cookie case, while the premise belief that this cookie is a fortune cookie has false counterparts, these counterparts are “solitary” in the sense that they do not co-exist with any counterpart of the other premise belief. Still, the safety theorist might argue, one could draw from such a solitary belief an inference to a conclusion belief that might act as a relevant counterpart of the original conclusion belief. To guarantee CI-COUNTER-CLOSURE, this counterpart of the conclusion belief would have to entail the solitary counterpart of the premise belief from which it is inferred. The most natural choice, then, is to think of the inference in question as a stuttering one: from the solitary counterpart premise belief, one infers a conclusion belief with the very same content.¹³

For instance, in some close case, Kim forms the false belief, of a French café gourmand cookie, that it is a fortune cookie, and then infers, redundantly, that it therefore is a fortune cookie. The latter belief could then serve as a false counterpart of the original conjunctive conclusion belief—just as needed.

This suggests yet a weaker coordination principle:

• WEAK PROXY CI-UPWARD COORDINATION. If belief α is solely arrived at by competent conjunction introduction from a belief β and other beliefs Γ, then, for any counterpart β′ of β, there is another counterpart β″ of β, with the same truth-value as β′, that co-exists with a counterpart α′ of α such that α′ entails β″.

As with INHERITANCE, some might think that the present proposal stretches the notion of similarity beyond plausibility. It is prima facie unclear why a conclusion belief inferred from some premise belief by a stuttering inference should be counted as similar to a conjunctive conclusion belief inferred from several premises, even though the former’s premise belief is similar to one of the latter’s premise beliefs. However, just as we argued in the context of corresponding worries about INHERITANCE, the safety theorist may, perhaps, have the resources to allay such worries.

Indeed, there are more pressing issues for the safety theorist who finds WEAK PROXY CI-UPWARD COORDINATION tempting. For, as it turns out, the present proposal faces a revenge contagion problem.

Suppose you believe that the building in front of you is a church, which it is, but mistake one of its quatrefoil-adorned spandrels for a roundel-adorned one and form the conjunctive belief that it is a church with a roundel-adorned spandrel, which happens to be false because this church does not have any roundel on its spandrels. In a similar case, you believe similarly, of a nearby church, that it is a church. However, that church is a Romanesque church, and Romanesque churches couldn´t have any spandrels ornamented with Gothic tracery sculpture such as quatrefoils or roundels. We submit that this counterpart of your original church-belief is a solitary one: there could not be a co-existing counterpart of your original premise belief that the building in front of you has a roundel-adorned spandrel.

Then, by WEAK PROXY CI-UPWARD COORDINATION, there would have to be a case in which a counterpart of your true premise belief that the building is a church is used as a premise of a stuttering inference whose conclusion belief is a counterpart of your original conclusion belief. However, on the safety conception, symmetry holds, so your original false conclusion belief is itself a counterpart of the stuttering inference’s conclusion belief. Thus, the safety theorist is committed to denying that the latter constitutes knowledge. Not only is this surprising, but it further commits the safety theorist to an unpalatable disjunction, namely that either the stuttering inference in question fails to preserve knowledge, or the solitary counterpart of one’s true premise belief fails to constitute knowledge (see Fig. 4).

Fig. 4

The contagion problem for WEAK CI-UPWARD COORDINATION. The true “church” premise belief has a solitary counterpart at w₂, which must be upward coordinated by a proxy at some world w₃. However, no such proxy co-exists with a counterpart of the “roundel” premise belief, so the premise belief’s counterpart at w₃ can at best serve as a premise belief for a stuttering inference whose conclusion belief is a counterpart of the original conclusion belief. By symmetry, any such conclusion belief as a false counterpart

The first horn would require the safety theorist to either reject a principle of closure under competent stuttering inference—a move even more egregious than rejecting CE-CLOSURE—or to claim that in these scenarios, none of the false conclusion belief’s counterparts that result from a stuttering inference can be the result of a competent deduction. The second horn would require them to claim that, in these scenarios, the solitary counterparts of a true premise belief cannot constitute knowledge if they serve as inputs for a stuttering inference. One could of course pick a different horn for any one of the conclusion belief’s counterparts that are arrived at by a stuttering inference, but this would appear to be even more arbitrary. Recall that your original premise belief that the building is a church was true, and for all we said, could constitute knowledge. It is utterly unclear why, in any close case where one similarly believes that a building is a church and forms a conclusion belief by a stuttering inference from it, but where one couldn’t have a counterpart of the other premise belief, one’s church-belief wouldn’t constitute knowledge, or one couldn’t competently draw the stuttering inference, or the inference wouldn’t preserve knowledge.

Accordingly, given the symmetry of similarity, WEAK PROXY CI-UPWARD COORDINATION commits friends of the safety conception of knowledge to wildly implausible claims. We conclude that endorsing WEAK PROXY CI-UPWARD COORDINATION is not a way for friends of the safety conception of knowledge to validate CI-COUNTER-CLOSURE either.

6 Conclusion

Let us take stock. According to the safety conception of knowledge, a belief is knowledge iff all its counterparts are true, where a belief is a counterpart of another iff it is similar to it. The safety conception of knowledge not only promises to vindicate intuitions we might have both about Gettier cases and about the implications of sceptical scenarios, but moreover to give us insight into the structure of knowledge by explaining—inter alia in terms of features of its preferred counterpart relation—what the validity of prominent principles of knowledge requires.

We saw that two independently plausible theses—viz. the NO-BOOTSTRAPPING CONSTRAINT and CE-CLOSURE—force acceptance of CI-COUNTER-CLOSURE. According to the NO-BOOTSTRAPPING CONSTRAINT, one cannot bootstrap one’s beliefs into knowledge by a sequence of conjunction introduction and elimination steps, however competent one may be in drawing these inferences. CE-CLOSURE is the thesis that knowledge is closed under competent conjunction elimination, and CI-COUNTER-CLOSURE is the thesis that knowledge is counter-closed under sole competent conjunction introduction. We could appreciate that the first two theses imply the third quite independently from any assumptions about the connection between knowledge and safe belief.

We proceeded to investigate what the safety conception of knowledge has to say about the validity of CE-CLOSURE and CI-COUNTER-CLOSURE—in instructive ways that exploit features of its counterpart relation and other relations such as entailment and competent deduction and their interaction. This led us to devise a formal framework and to prove important correspondence results. Given the formal framework suggested, it turned out that, to validate CE-CLOSURE and CI-COUNTER-CLOSURE, the safety conception of knowledge must postulate suitable coordination principles: CE-DOWNWARD COORDINATION and CI-UPWARD COORDINATION. A more rigorous demonstration of generalisations of these results was relegated to the Appendix.

However, of these two coordination principles, the latter makes a rather strong assumption that stands in need of further backing: it demands that any counterpart of a premise belief co-exists with some counterpart of the conclusion belief. At first sight, this seems like an overly strong demand: in cases in which there is a counterpart to a premise belief, no conclusion might be drawn. To address this worry, we introduced INHERITANCE—a principle according to which counterparts of premise beliefs themselves serve as counterparts for the relevant conclusion belief. This already threatened to stretch the notion of similarity beyond plausibility. But we let that thought pass. More damningly for the safety theorist, acceptance of INHERITANCE proved a calamity, for the following reason: the safety conception’s counterpart relation—similarity—is by its very nature symmetric. Under symmetry, INHERITANCE leads to the disastrous result that one cannot competently deduce a false conjunction from a set of premises one of which is known. This is what we called contagion.

The finding then prompted consideration of several possible countermoves, none of which successful in the end. These countermoves departed from the idea that CI-UPWARD COORDINATION was never a natural contender to begin with and that, in the light of the aforementioned correspondence results, our formal framework would need to be suitably extended to capture a further relation besides counterparthood, entailment, and relations of competent deduction.

In a first go, we thus considered replacing CI-UPWARD COORDINATION by a weaker principle which did, however, founder in the light of examples of the same broad kind as Kripke’s famous red barn example. For, the replacement in question—PROXY CI-UPWARD COORDINATION—requires that false counterparts of one premise belief must co-exist with counterparts of any other. Yet, the problematic examples precisely involve scenarios in which the false counterparts of a premise belief cannot do so: they are bound to be “solitary”.

Next, we considered introducing yet a weaker principle, WEAK PROXY CI-UPWARD COORDINATION, that lifted that requirement. Like INHERITANCE, WEAK PROXY CI-UPWARD COORDINATION requires a somewhat strained reading of similarity. But, as before, this point proved marginal, as did the observation that WEAK PROXY CI-UPWARD COORDINATION makes somewhat artificial assumptions about epistemic agents, viz., that they could easily engage in stuttering inferences. The chief problem that WEAK PROXY CI-UPWARD COORDINATION poses for the safety conception of knowledge rather is that it again gives rise to a contagion problem: given the symmetry of similarity, one’s false conclusion beliefs are deemed counterparts of the beliefs that result from competent stuttering inferences from solitary counterparts of one’s true premise beliefs. This has the consequence that the latter counterparts cannot constitute knowledge—an ad hoc ruling that lacks any independent rationale.

The NO-BOOTSTRAPPING CONSTRAINT is non-negotiable. In its light, the very intuitive principle of CE-CLOSURE forces acceptance of CI-COUNTER-CLOSURE. If the safety conception doesn’t have the resources to validate the latter, this calls into question its ability to validate the former. Both principles are rather weak: standard arguments against full-blown closure under competent deduction or against full-blown counter-closure under competent deduction would seem to leave them unaffected. We conclude that not only does the safety conception of knowledge appear unable to shed any interesting light on prominent principles of knowledge, but, worse, it appears positively inimical to the most plausible ones.

Whither now? We saw that many of the problems we diagnosed arose because of the safety theorist’s construal of counterparthood as a symmetric relation. This is not an optional feature of the safety conception of knowledge, though, as similarity is by its very nature symmetric. It may thus seem that a natural way forward is to retain the overall shape of that conception but replace similarity by another, non-symmetric counterpart relation. Consider, for instance, a normality-based conception according to which a belief’s counterparts are beliefs at least as normal as that belief, in some suitable sense of ‘normal’. Suppose the following holds:

• ABNORMALITY INHERITANCE. If a belief is deduced by competent conjunction introduction from some other beliefs, each premise belief is at least as normal as it.

(In other words, the conclusion belief is comparable in normality to each premise belief, and cannot be more normal than the least normal premise belief.) Together with the normality-based conception of counterparthood, ABNORMALITY INHERITANCE entails INHERITANCE (and thereby WEAK PROXY CI-UPWARDS COORDINATION): any counterpart of some premise belief is at least as normal as that belief, which is in turn at least as normal as the conclusion belief, hence by transitivity, it is a counterpart of the conclusion belief. Hence, it would validate CI-COUNTER-CLOSURE. It remains to be seen whether a plausible normality-based conception can uphold ABNORMALITY INHERITANCE, or if another non-symmetric counterpart account can make INHERITANCE or WEAK PROXY CI-UPWARDS COORDINATION more palatable. It likewise remains to be seen whether these accounts validate INHERITANCE not only for conjunction introduction, but for competent deduction more generally. If so, they will validate counter-closure for competent deduction in general, which may or may not be a welcome result.

Appendix

We use simple languages with variables ranging over token beliefs and predicates corresponding to truth, knowledge, and deductive and entailment relations among token beliefs. Thus, factivity, the idea that knowledge entails truth, will be stated $Kx\to Tx$ instead of the more familiar $Kp\to p$. These languages are congenial to our project because token beliefs figure centrally in common formulations of safety (a belief in a given case, i.e. at a given world and time, is similar to some belief in some other case) and of closure and counter-closure principles (if a belief in q is competently deduced from a belief in p, then the former constitutes knowledge if the latter does).

It would be relatively straightforward to extend our language to recover standard modal operators. One could first introduce binary operators taking a variable for a belief and a formula, e.g., $Kxp$ for “x is a belief that constitutes knowledge that $p$” and introduce standard epistemic operators as existentially quantifying over belief tokens, e.g., $Kp$ abbreviates $\exists xKxp$. These are unnecessary to state our results, however, so we leave them out.

We will also use variables $X,Y,\dots$ for sets of beliefs. This allows us to express many-one relations between premise beliefs and conclusion beliefs without using cumbersome variadic operators. A membership predicate could be introduced but we don’t need it.

Our languages are:

• ${\mathcal{L}}^{BC}$ . A propositional language with atomic formulas $K\gamma$, $T\gamma$, for any individual variable $\gamma$.

• ${\mathcal{L}}^{BCDE}$ . A propositional language with atomic formulas $K\gamma$, $K\Gamma$ (knowledge predicate for individual beliefs and sets of beliefs), $T\gamma$, $T\Gamma$ (truth predicate for individual beliefs and sets of beliefs) and $D\Gamma \gamma$ (arbitrary deduction relation between sets of premise beliefs and conclusion belief), where $\gamma$ is any individual variable and $\Gamma$ any plural (set) variable.

Instead of introducing quantifiers, we’ll simply state principles of interest as schemas:

• Factivity. $Kx\to Tx$

• Closure. $DXx\to \left(KX\to Kx\right)$

• Counter-closure. $DXx\to \left(Kx\to KX\right)$

A Belief-Counterparts frame (BC frame) $\mathcal{F}=\langle \mathcal{W},\mathcal{B},\mathcal{C}\rangle$ is given by:

• $\mathcal{W}$ is a non-empty set (worlds)

• $\mathcal{B}={\bigcup }_{w\in \mathcal{W}}{\mathcal{B}}_{i}$ a family of disjoint sets indexed by $\mathcal{W}$ (token beliefs). For each belief $b\in \mathcal{B}$ we write ${w}_{b}$ for its index world.

• $\mathcal{C}\subseteq \mathcal{B}\times \mathcal{B}$ a relation over $\mathcal{B}$ (epistemic counterparthood)

A model $\mathcal{M}=\langle \mathcal{F},\mathcal{A},\mathcal{V}\rangle$ based on $\mathcal{F}$ is given by:

• $\mathcal{V}$ an interpretation that associates each variable $\gamma$ of ${\mathcal{L}}^{BC}$ with a token belief:

• $\mathcal{V}\left(\alpha \right)\in \mathcal{B}$.

• $\mathcal{A}$ an assignment function that associates each token belief $b\in \mathcal{B}$ with a set of worlds: $\mathcal{A}\left(b\right)\subseteq \mathcal{W}$. $\mathcal{A}\left(b\right)$ represent the token belief’s truth conditions, i.e., the set of worlds at which its content is true.

Truth of ${\mathcal{L}}^{BC}$ formulas in a BC model is given by:

• ${\mathcal{M}},w \vDash T\gamma$ iff ${w}_{\mathcal{V}\left(\gamma \right)}\in \mathcal{A}\left(\mathcal{V}\left(\gamma \right)\right)$

• ${\mathcal{M}},w \vDash K\gamma$ iff for any $b$ s.th. $\langle \mathcal{V}\left(\gamma \right),b\rangle \in \mathcal{C}$, ${w}_{b}\in \mathcal{A}\left(b\right)$.

and as usual for the propositional connectives. It is easy to see that the world parameter is redundant: because our formulas directly talk about the properties of world-bound belief tokens, the facts they express are not world-dependent. We have included it to show that the language could be expanded to express world-dependent claims too, e.g., to quantify over the current world’s beliefs.

Proposition 1

Factivity is valid on a BC frame iff $\mathcal{C}$ is reflexive.

Proof

The LtR direction is immediate. For RtL, suppose a frame isn’t reflexive: for some $b$, $\langle b,b\rangle \notin \mathcal{C}$. Consider the model given by ${\mathcal{A}}\left( b \right) = \emptyset$, $\mathcal{A}\left(c\right)=\mathcal{W}$ for any $c\ne b$, and some $\mathcal{V}$ such that $\mathcal{V}\left(x\right)=b$. For any $b\mathrm{^{\prime}}$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$, ${w}_{b\mathrm{^{\prime}}}\in \mathcal{A}\left(b\mathrm{^{\prime}}\right)=\mathcal{W}$, but ${w}_{b}\notin \mathcal{A}\left(b\right)$, so $Kx$ holds but $Tx$ fails in the model.

A Belief-Counterparts-Deduction-Entailment frame (BCDE frame) $\mathcal{F}=\langle \mathcal{W},\mathcal{B},\mathcal{C},\mathcal{D},\mathcal{E}\rangle$ is given by extending a BC frame with:

• $\mathcal{E}\subseteq \mathcal{P}\mathcal{B}\times \mathcal{B}$ a relation between sets of beliefs and beliefs that satisfies Reflexivity, Monotonicity, and Cut (entailment). That is, where $b,c\in \mathcal{B}$ and $B,C\subseteq \mathcal{B}$:

  • Reflexivity. $\langle \{b\},b\rangle \in \mathcal{E}$

  • Monotonicity. If $\langle B,b\rangle \in \mathcal{E}$ and $B\subseteq C$ then $\langle C,b\rangle \in \mathcal{E}$.

  • Cut. If $\langle B,c\rangle \in \mathcal{E}$ and for each $b\in B$ there is a ${C}_{b}$ such that $\langle {C}_{b},b\rangle \in \mathcal{E}$ then $\langle {\bigcup }_{b\in B}{C}_{b},c\rangle \in \mathcal{E}$.

• $\mathcal{D}\subseteq \mathcal{E}$ a relation between sets of beliefs and beliefs that requires entailment and satisfies Co-worldliness (deduction).

  • Co-worldliness. If $\langle B,b\rangle \in \mathcal{D}$ then ${w}_{b\mathrm{^{\prime}}}={w}_{b}$ for any $b\mathrm{^{\prime}}\in B$.

Optionally, we may require $\mathcal{D}$ to satisfy Irreflexivity ($\langle \{b\},b\rangle \notin \mathcal{D}$) and Cut.

A model $\mathcal{M}=\langle \mathcal{F},\mathcal{A},\mathcal{V}\rangle$ based on $\mathcal{F}$ is given by:

• $\mathcal{V}$ an interpretation such that $\mathcal{V}\left(\gamma \right)\in \mathcal{B}$ and $V\left(\Gamma \right)\subseteq \mathcal{B}$ for any individual variable $\gamma$ and plural variable $\Gamma$.

• $\mathcal{A}$ an assignment function as before, with the added constraint that it respects the frame’s entailment relations: if $\langle B,c\rangle \in \mathcal{E}$ then ${\bigcap }_{b\in B}\mathcal{A}\left(b\right)\subseteq \mathcal{A}\left(c\right)$.

That is, if some beliefs jointly entail another, then the latter’s content is true at any world at which the contents of all of the former are. It is easy to see that any frame affords models satisfying this constraint—consider for instance the assignment that assigns the same truth set to all belief tokens.

Truth of ${\mathcal{L}}^{BCDE}$ formulas in a BCDE model is given by:

• ${\mathcal{M}},w \vDash T\gamma$ iff ${w}_{\mathcal{V}\left(\gamma \right)}\in \mathcal{A}\left(\mathcal{V}\left(\gamma \right)\right)$

• ${\mathcal{M}},w \vDash T\Gamma$ iff for any $b\in \mathcal{V}\left(\Gamma \right)$, ${w}_{b}\in \mathcal{A}\left(b\right)$.

• ${\mathcal{M}},w\vDash K\gamma$ iff for any $b$ s.th. $\langle \mathcal{V}\left(\gamma \right),b\rangle \in \mathcal{C}$, ${w}_{b}\in \mathcal{A}\left(b\right)$.

• ${\mathcal{M}},w \vDash K\Gamma$ iff for any $b\in \mathcal{V}\left(\Gamma \right)$, for any $c$ s.th. $\langle b,c\rangle \in \mathcal{C}$, ${w}_{c}\in \mathcal{A}\left(c\right)$.

• ${\mathcal{M}},w \vDash D\Gamma \gamma$ iff $\langle \mathcal{V}\left(\Gamma \right),\mathcal{V}\left(\gamma \right)\rangle \in \mathcal{D}$.

• And as usual for the propositional connectives.

Again, relativization to worlds is superfluous here but would be needed in a richer language.

Definitions

A frame is downward coordinated iff for any $B,b$ s.th. $\langle B,c\rangle \in \mathcal{D}$, for any $c\mathrm{^{\prime}}$ s.th. $\langle c,c\mathrm{^{\prime}}\rangle \in \mathcal{C}$, there is a set $B\mathrm{^{\prime}}$ s.th. ${w}_{b\mathrm{^{\prime}}}={w}_{c}$ for any $b\mathrm{^{\prime}}\in B$, $\langle B\mathrm{^{\prime}},c\mathrm{^{\prime}}\rangle \in \mathcal{E}$, and for any $b\mathrm{^{\prime}}\in B\mathrm{^{\prime}}$ there is a $b$ in $B$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$. That is, whenever $c$ is deduced from $B$, any counterpart $c\mathrm{^{\prime}}$ of the conclusion belief $c$ is jointly entailed by a co-worldly set of beliefs $B\mathrm{^{\prime}}$ that are counterparts of some beliefs in $B$.

A frame is upward coordinated iff for any $B,c$ s.th. $\langle B,c\rangle \in \mathcal{D}$, for any $b\in B$, for any $b\mathrm{^{\prime}}$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$, there is a set $C\mathrm{^{\prime}}$ s.th. ${w}_{c\mathrm{^{\prime}}}={w}_{b\mathrm{^{\prime}}}$ for any $c\mathrm{^{\prime}}\in C\mathrm{^{\prime}}$, $\langle C\mathrm{^{\prime}},b\mathrm{^{\prime}}\rangle \in \mathcal{E}$ and for any $c\mathrm{^{\prime}}\in C\mathrm{^{\prime}}$, $\langle c,c\mathrm{^{\prime}}\rangle \in \mathcal{C}$. That is, whenever $c$ is deduced from $B$, any counterpart $b\mathrm{^{\prime}}$ of any premise belief $b$ in $B$ is jointly entailed by a co-worldly set of beliefs $C\mathrm{^{\prime}}$ that are counterparts of the conclusion belief $c$.

Proposition 2

Closure is valid on a BCDE frame $\mathcal{F}$ iff $\mathcal{F}$ is downward coordinated.

Counter-closure is valid on a BCDE frame $\mathcal{F}$ iff $\mathcal{F}$ is upward coordinated.

Proof. For the RtL direction of closure, suppose ${\mathcal{M}},w \vDash DXx$ and ${\mathcal{M}},w \vDash KX$ for some model $\mathcal{M}$ based on a downward coordinated frame $\mathcal{F}$ and some world $w$. Since $\mathcal{M},w\models DXx$, there are $B,c$ s.th.$\mathcal{V}\left(X\right)=B$, $\mathcal{V}\left(x\right)=c$ and $\langle B,c\rangle \in \mathcal{D}$. Let $c\mathrm{^{\prime}}$ be any such that $\langle c,c\mathrm{^{\prime}}\rangle \in \mathcal{C}$. By coordination, there is a set $B\mathrm{^{\prime}}$ s.th. ${w}_{b\mathrm{^{\prime}}}={w}_{c\mathrm{^{\prime}}}$ for any $b\mathrm{^{\prime}}\in B\mathrm{^{\prime}}$, $\langle B\mathrm{^{\prime}},c\mathrm{^{\prime}}\rangle \in \mathcal{E}$ and for any $b\mathrm{^{\prime}}\in B\mathrm{^{\prime}}$ there is a $b$ in $B$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$. Since$\left\langle {B^{\prime },c^{\prime }} \right\rangle \in {\mathcal{E}}$, ${\bigcap }_{b\mathrm{^{\prime}}\in B\mathrm{^{\prime}}}\mathcal{A}\left(b\mathrm{^{\prime}}\right)\subseteq \mathcal{A}\left(c\mathrm{^{\prime}}\right)$. Since ${\mathcal{M}},w \vDash KX$ and $\mathcal{V}\left(X\right)=B$, we have ${w}_{c\mathrm{^{\prime}}}={w}_{b\mathrm{^{\prime}}}\in \mathcal{A}\left(b\mathrm{^{\prime}}\right)$ for any $b\mathrm{^{\prime}}\in B\mathrm{^{\prime}}$. So, ${w}_{c\mathrm{^{\prime}}}\in \mathcal{A}\left(c\mathrm{^{\prime}}\right)$. Generalizing over $c\mathrm{^{\prime}}$, and since $\mathcal{V}\left(x\right)=c$, ${\mathcal{M}},w \vDash Kx$. Generalizing on $\mathcal{M},w$, $\mathcal{F} \vDash DXx \to \left( {KX \to Kx} \right)$.

For the LtR direction, suppose $\mathcal{F}$ is not downward coordinated. There are some $B,c$ s.th. $\langle B,c\rangle \in \mathcal{D}$ and some ${c}^{\mathrm{^{\prime}}}$ s.th. $\langle c,{c}^{\mathrm{^{\prime}}}\rangle \in \mathcal{C}$ but there is no set ${B}^{\mathrm{^{\prime}}}$ s.th. ${w}_{{b}^{\mathrm{^{\prime}}}}={w}_{{c}^{\mathrm{^{\prime}}}}$ for any ${b}^{\mathrm{^{\prime}}}\in {B}^{\mathrm{^{\prime}}}$, $\langle {B}^{\mathrm{^{\prime}}},{c}^{\mathrm{^{\prime}}}\rangle \in \mathcal{E}$ and for any ${b}^{\mathrm{^{\prime}}}\in {B}^{\mathrm{^{\prime}}}$ there is a $b$ in $B$ s.th. $\langle b,{b}^{\mathrm{^{\prime}}}\rangle \in \mathcal{C}$. Consider the model with $\mathcal{V}\left(X\right)=B,\mathcal{V}\left(x\right)=c$ and $\mathcal{A}$ s.th. $\mathcal{A}\left(d\right)=\mathcal{W}$ iff for some set ${B}^{\mathrm{^{\prime}}}$, ${w}_{{b}^{\mathrm{^{\prime}}}}={w}_{d}$ for any ${b}^{\mathrm{^{\prime}}}\in {B}^{\mathrm{^{\prime}}}$, $\langle {B}^{\mathrm{^{\prime}}},d\rangle \in \mathcal{E}$ and for any ${b}^{\mathrm{^{\prime}}}\in {B}^{\mathrm{^{\prime}}}$ there is a $b$ in $B$ s.th. $\langle b,{b}^{\mathrm{^{\prime}}}\rangle \in \mathcal{C}$; otherwise ${\mathcal{A}}\left( d \right) = \emptyset$. By construction, $w_{{c^{\prime}}} \notin {\mathcal{A}}\left( {c^{\prime}} \right) = \emptyset$, so, letting $w$ be some arbitrary world, ${\mathcal{M}},w \nvDash Kx$. For any $b\in B$, any ${b}^{\mathrm{^{\prime}}}$ s.th. $\langle b,{b}^{\mathrm{^{\prime}}}\rangle \in \mathcal{C}$, we have $\langle {b}^{\mathrm{^{\prime}}},{b}^{\mathrm{^{\prime}}}\rangle \in \mathcal{E}$ by the reflexivity of $\mathcal{E}$ so by the construction of $\mathcal{A}$, ${w}_{{b}^{\mathrm{^{\prime}}}}\in \mathcal{A}\left({b}^{\mathrm{^{\prime}}}\right)=\mathcal{W}$. Generalizing on $b$ and ${b}^{\mathrm{^{\prime}}}$, ${\mathcal{M}},w \vDash KX$. Since $\langle B,c\rangle \in \mathcal{D}$, ${\mathcal{M}},w \vDash DXx$. So, ${\mathcal{M}},w \nvDash DXx \to \left( {KX \to Kx} \right)$. We still need to check that $\mathcal{A}$ is proper, i.e., respects entailment relations. Let $D,e$ be any such that $\langle D,e\rangle \in \mathcal{E}$. By the construction of $\mathcal{A}$, $\mathcal{A}\left(d\right)=\mathcal{W}$ or $\emptyset$ for any $d\in D$. If ${\mathcal{A}}\left( d \right) = \emptyset$ for some $d\in D$, then $\cap_{d \in D} {\mathcal{A}}\left( d \right) = \emptyset \subseteq {\mathcal{A}}\left( e \right)$. Otherwise, $\mathcal{A}\left(d\right)=\mathcal{W}$ for any $d\in D$. By the construction of $\mathcal{A}$, this means that for any $d\in D$ there is some set $B{\mathrm{^{\prime}}}_{d}$ s.th. ${w}_{b\mathrm{^{\prime}}}={w}_{d}$ for any $b\mathrm{^{\prime}}\in B{\mathrm{^{\prime}}}_{d}$, $\langle B{\mathrm{^{\prime}}}_{d},d\rangle \in \mathcal{E}$ and for any $b\mathrm{^{\prime}}\in B{\mathrm{^{\prime}}}_{d}$ there is a $b$ in $B$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$. Since $\mathcal{E}$ satisfies Cut, $\langle B{\mathrm{^{\prime}}}_{d},d\rangle \in \mathcal{E}$ for any $d\in D$ and $\langle D,e\rangle \in \mathcal{E}$, we have $\langle {\bigcup }_{d\in D}B{\mathrm{^{\prime}}}_{d},e\rangle \in \mathcal{E}$. Since for any $b\mathrm{^{\prime}}\in {\bigcup }_{d\in D}B{\mathrm{^{\prime}}}_{d}$ there is a $b$ in $B$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$, by the construction of $\mathcal{A}$ we have $\mathcal{A}\left(e\right)=\mathcal{W}$. So ${\bigcap }_{d\in D}\mathcal{A}\left(d\right)\subseteq \mathcal{A}\left(e\right)=\mathcal{W}$. Hence $\mathcal{A}$ is proper, and closure is not valid on $\mathcal{F}$.

The RtL direction of counter-closure is analogue to that of closure. For the LtR direction, suppose $\mathcal{F}$ is not upward coordinated. For some $B,c$ s.th. $\langle B,c\rangle \in \mathcal{D}$, some $b\in B$ and some $b\mathrm{^{\prime}}$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$, there is no set $C\mathrm{^{\prime}}$ s.th. ${w}_{c\mathrm{^{\prime}}}={w}_{b\mathrm{^{\prime}}}$ for any $c\mathrm{^{\prime}}\in C\mathrm{^{\prime}}$, $\langle C\mathrm{^{\prime}},b\mathrm{^{\prime}}\rangle \in \mathcal{E}$ and for any $c\mathrm{^{\prime}}\in C\mathrm{^{\prime}}$, $\langle c,c\mathrm{^{\prime}}\rangle \in \mathcal{C}$. Consider the model $\mathcal{M}$ with $\mathcal{V}\left(X\right)=B,\mathcal{V}\left(x\right)=c$ and $\mathcal{A}$ s.th. $\mathcal{A}\left(d\right)=\mathcal{W}$ iff for some set $C\mathrm{^{\prime}}$, ${w}_{c\mathrm{^{\prime}}}={w}_{b\mathrm{^{\prime}}}$ for any $c\mathrm{^{\prime}}\in C\mathrm{^{\prime}}$, $\langle C\mathrm{^{\prime}},d\rangle \in \mathcal{E}$ and for any $c\mathrm{^{\prime}}\in C\mathrm{^{\prime}}$, $\langle c,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$; otherwise ${\mathcal{A}}\left( d \right) = \emptyset$. By construction, $w_{{b{^{\prime}}}} \notin {\mathcal{A}}\left( {b{^{\prime}}} \right) = \emptyset$, and so, letting $w$ be some arbitrary world, ${\mathcal{M}},w \nvDash KX$. For any $c\mathrm{^{\prime}}$ s.th. $\langle c,c\mathrm{^{\prime}}\rangle \in \mathcal{C}$, we have ${w}_{c\mathrm{^{\prime}}}={w}_{c\mathrm{^{\prime}}}$ and $\left\langle {\left\{ {c^\prime } \right\},c^\prime } \right\rangle \in {\mathcal{E}}$ by the reflexivity of $\mathcal{E}$, hence ${w}_{c\mathrm{^{\prime}}}\in \mathcal{A}\left(c\mathrm{^{\prime}}\right)=\mathcal{W}$ by the construction of $\mathcal{A}$. Generalizing on $c\mathrm{^{\prime}}$, ${\mathcal{M}},w \vDash Kx$. Since $\langle B,c\rangle \in \mathcal{D}$, ${\mathcal{M}},w \vDash DXx$. The proof that $\mathcal{A}$ is proper follows the same steps as before. Hence counter-closure is not valid on $\mathcal{F}$.

The proofs hold even if $\mathcal{D}$ is irreflexive or satisfies Cut. The models used to establish LtR directions, in particular, are still available if these constraints are imposed. So, the results still hold in the classes of frames that impose either or both of these conditions.

The proofs also hold if $\mathcal{C}$ is required to be reflexive, symmetric and/or transitive. Downward and upward coordination can be satisfied in conjunction with any combination of these constraints on $\mathcal{C}$, so the RtL directions hold non-vacuously. The models used to establish LtR directions are available irrespective of these properties of $\mathcal{C}$, so these directions hold in any of these subclasses too.

Factivity in BCDE frames. In BCDE frames, the reflexivity of $\mathcal{C}$ is not strictly necessary for factivity. That is because these frames can fix entailment relations between beliefs, which allows factivity to hold just when every belief is entailed by some co-worldly counterparts. One might worry that this makes the frames less significant, as unlike BC frames, they don’t capture the canonical way for safety to deliver factivity. However, it can be shown that this weakening of the necessary condition for factivity is immaterial in the sense that frames that satisfy factivity in this weaker way are pointwise equivalent to their reflexive closure, hence indistinguishable from reflexive ones.

Let a BCDE frame be quasi-reflexive iff any belief is entailed by some co-worldly counterparts of itself: for any $b\in \mathcal{B}$, there is a $B$ s.th. ${w}_{b\mathrm{^{\prime}}}={w}_{b}$ for any $b\mathrm{^{\prime}}\in B$, $\langle B,b\rangle \in \mathcal{E}$ and for any $b\mathrm{^{\prime}}\in B$, $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$. Note that, since $\mathcal{E}$ is reflexive, frames where $\mathcal{C}$ is reflexive are quasi-reflexive. Let reflexive closure ${\mathcal{M}}^{+}$ of a model $\mathcal{M}$ be the result of replacing the counterparthood relation $\mathcal{C}$ with its reflexive closure ${\mathcal{C}}^{+}=\mathcal{C}\cup \{\langle b,b\rangle :b\in \mathcal{B}\}$. Note that ${\mathcal{M}}^{+}$ is a proper model, since the requirement that $\mathcal{A}$ respects entailment relations is independent of $\mathcal{C}$.

Proposition 3

Factivity is valid on a BCDE frame $\mathcal{F}$ iff $\mathcal{F}$ is quasi-reflexive.

Every quasi-reflexive frame $\mathcal{M}$ is pointwise equivalent to its reflexive closure ${\mathcal{M}}^{+}$.

Proof

The RtL direction is straightforward. For the LtR direction, suppose $\mathcal{F}$ is not quasi-reflexive. For some $b$, there is no $B$ s.th. ${w}_{{b}^{\mathrm{^{\prime}}}}={w}_{b}$ for any ${b}^{\mathrm{^{\prime}}}\in B$, $\langle B,b\rangle \in \mathcal{E}$ and for any ${b}^{\mathrm{^{\prime}}}\in B$, $\langle b,{b}^{\mathrm{^{\prime}}}\rangle \in \mathcal{C}$. Consider the model with $\mathcal{V}\left(x\right)=b$ and $\mathcal{A}$ s.th. $\mathcal{A}\left(c\right)=\mathcal{W}$ iff for some set $B$, ${w}_{{b}^{\mathrm{^{\prime}}}}={w}_{c}$ for any ${b}^{\mathrm{^{\prime}}}\in B$, $\langle B,c\rangle \in \mathcal{E}$ and for any ${b}^{\mathrm{^{\prime}}}\in B$, $\langle b,{b}^{\mathrm{^{\prime}}}\rangle \in \mathcal{C}$. The proof that $\mathcal{A}$ is proper follows the same steps as before. By construction, ${\mathcal{V}}\left( b \right) = \emptyset$, so, where $w$ is some arbitrary world, ${\mathcal{M}},w \nvDash Tx$. Let $b\mathrm{^{\prime}}$ be any such that $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$. By the reflexivity of $\mathcal{E}$, we have $\left\langle {\left\{ {b^{\prime }} \right\},b^{\prime } \in {\mathcal{E}}} \right\rangle$, so by the construction of $\mathcal{A}$, ${w}_{b\mathrm{^{\prime}}}\in \mathcal{A}\left(b\mathrm{^{\prime}}\right)=\mathcal{W}$. Generalizing on $b\mathrm{^{\prime}}$, ${\mathcal{W}},w \vDash Kx$. Thus, factivity is not valid on $\mathcal{F}$.

For pointwise equivalence, we first establish a lemma: in quasi-reflexive models, all the counterparts of a belief are true iff all its counterparts and itself are true. That is, for any given belief $b$, ${w}_{b\mathrm{^{\prime}}}\in \mathcal{A}\left(b\mathrm{^{\prime}}\right)$ for any $b\mathrm{^{\prime}}$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$ if and only if ${w}_{b\mathrm{^{\prime}}}\in \mathcal{A}\left(b\mathrm{^{\prime}}\right)$ for any $b\mathrm{^{\prime}}$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in {\mathcal{C}}^{+}$. The RtL direction is immediate from the fact that if $b\mathrm{^{\prime}}$ is s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$, then $\langle b,b\mathrm{^{\prime}}\rangle \in {\mathcal{C}}^{+}$. For the RtL direction, suppose ${w}_{b\mathrm{^{\prime}}}\in \mathcal{A}\left(b\mathrm{^{\prime}}\right)$ for any $b\mathrm{^{\prime}}$ s.th. $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$; we need to show that ${w}_{b}\in \mathcal{A}\left(b\right)$. By quasi-reflexivity, there is a $B$ s.th. ${w}_{b\mathrm{^{\prime}}}={w}_{b}$ for any $b\mathrm{^{\prime}}\in B$, $\langle B,b\rangle \in \mathcal{E}$ and for any $b\mathrm{^{\prime}}\in B$, $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$. Since $\langle B,b\rangle \in \mathcal{E}$, ${\bigcap }_{b\mathrm{^{\prime}}\in B}\mathcal{A}\left(b\mathrm{^{\prime}}\right)\subseteq \mathcal{A}\left(b\right)$. Since $\langle b,b\mathrm{^{\prime}}\rangle \in \mathcal{C}$ for any $b\mathrm{^{\prime}}\in B$, ${w}_{b}={w}_{b\mathrm{^{\prime}}}\in \mathcal{A}\left(b\mathrm{^{\prime}}\right)$ for any for any $b\mathrm{^{\prime}}\in B$, so ${w}_{b}\in {\bigcap }_{b\mathrm{^{\prime}}\in B}\mathcal{A}\left(b\mathrm{^{\prime}}\right)\subseteq \mathcal{A}\left(b\right)$, as desired. From the lemma it follows that ${\mathcal{M}},w \vDash Kx$ iff ${\mathcal{M}}^{ + } ,w \vDash Kx$, and similarly for $KX$. A survey of the semantics shows that these are the only places where $\mathcal{C}$ plays a role, so the models are pointwise equivalent.

Hence, making a quasi-reflexive frame fully reflexive does not make a difference. In particular, it has no effect on whether the frame is downward or upward coordinated. This follows from pointwise equivalence and the correspondence results and can also be worked out from the definitions of quasi-reflexivity, downward coordination and upward coordination. Hence for all intents and purposes, reflexivity can still be regarded as the natural condition for factivity in BCDE frames.