1 Introduction

Very long baseline interferometry (VLBI) is a unique space-geodetic technique that combines globally distributed radio telescopes to observe signals from celestial radio sources, typically quasars. VLBI has a wide range of applications, and it is an important observing technique for astronomy, astrometry, and geodesy. A non-exhaustive list of its uses includes imaging (astronomy) and determining positions and movement (astrometry) of the extra-galactic radio sources, and measuring the position of the observing antennas (geodesy) (see, e.g. Sovers et al. 1998; Schuh and Behrend 2012). For geodesy, VLBI is the only technique capable of fully determining Earth’s orientation in space, providing a link between the Terrestrial and Celestial Reference Frames. Contributions from these different applications of VLBI are not only confined to their specific fields. For accurate geodetic VLBI observations, precise knowledge of source positions and structure is necessary.

The International VLBI Service for Geodesy and Astrometry (IVS) (Nothnagel et al. 2017) is a service of the International Association of Geodesy (IAG) (Poutanen and Rózsa 2020). It coordinates the geodetic VLBI observations, correlation, and analysis. The main operational geodetic observing programs of IVS have been the bi-weekly 24-h rapid turnaround sessions and daily 1-h intensive sessions. The former is targeted to determine station positions and Earth Orientation Parameters (EOPs), while the latter provides daily updates on the UT1-UTC difference. Typically, both rapid and intensive sessions have been observed on dual S/X-band frequency setup.

In order to meet the growing need for more accurate reference frames, a next-generation broadband VLBI Geodetic Observing System (VGOS) (Niell et al. 2006, 2018) is currently being deployed globally. VGOS is a component of the IVS and serves as the VLBI contribution to the Global Geodetic Observing System (GGOS) of the IAG. A great deal of effort has been made towards making VGOS operational, and in recent years, VGOS observations have been carried out alongside, and at times simultaneously, with the S/X observing network, which in this context is often referred to as a legacy S/X system.

The operational goals for VGOS are to provide 24/7 monitoring of station positions and Earth Orientation Parameters (EOPs) (Petit and Luzum 2010) together with 24-h turnaround time for initial geodetic products. In terms of performance, VGOS goal is to provide station positions and velocities with 1 mm and 0.1 mm/year accuracy, respectively (Niell et al. 2006; Petrachenko et al. 2009). Reaching these accuracy goals requires that the sources of random and systematic errors are understood and accounted for.

The delays and delay rates observed by geodetic VLBI have several factors that contribute to the total error budget of the observations. Some of the main ones include atmospheric delays (troposphere and ionosphere), station clock instabilities, cable delays, instrumental errors, unmodeled geophysical effects, thermal and gravitational deformation of the antenna, offsets in a priori station positions, errors in EOPs, measurement noise, and radio source structure.

The different geodetic VLBI analysis software packages handle these errors by a combination of modelling (e.g. geophysical effects), estimation (e.g. zenith wet delays, clocks), using in situ measurements (e.g. cable delays), and modelling the measurement noise by some stochastic model (e.g. constant additive noise). However, delay errors due to source structure have typically not been accounted for in routine geodetic VLBI at the analysis stage. The radio sources are treated as point-like, and while for very compact and stable sources this could be a valid assumption, in reality, most of the sources exhibit time- and frequency-dependent extended structure (e.g. Lister et al. 1996; Savolainen et al. 2006), which have an effect on the observed group delay (Charlot 1990). The effective magnitude of the source structure effect varies based on the intrinsic structure and the relative orientation between the baseline and the source.

Supermassive black holes that accrete gas from their surroundings become active (Active Galactic Nuclei, AGN) and can subsequently form a pair of jets of magnetized plasma that are ejected from the immediate vicinity of the black hole at relativistic speed and can extend far beyond the confines of the host galaxy—up to distances of hundreds of kiloparsecs (for a recent review, see Blandford et al. 2019). Depending on the orientation to an observer, these jets can appear to the observer as prominent directional structures in the source. An example of such a jet as seen by VLBI is illustrated in Fig. 1. Specifically, in the case of so-called blazars, whose jets are seen in a small angle with respect to the line-of-sight, relativistic Doppler boosting greatly enhances the observed brightness of the approaching jet while diminishing the observed brightness from the receding jet, thus creating an apparently one-sided jet structure. Here it is important to note that the jet features in the VLBI scale can vary significantly with both time and frequency. Thus, an image obtained in the past may not correspond to what the source looks like in the present or at a different observing frequency. With high enough resolution, most blazars are expected to feature this type of jet-structure (for VLBI survey results, see, e.g. Lister et al. 1996; Popkov et al. 2021; Petrov 2021). In some cases, the source structure can change much faster than within a time span of years. An example of such a source is PKS B1144-379, which has been studied in detail in Said et al. (2020, 2021). In such cases, VLBI images cannot be used for correcting structure effects if they are more than a few months old.

Fig. 1
figure 1

Quasar 1803+784 observed at 6.616 GHz with a VGOS array consisting of GGAO12M, ISHIOKA, KOKEE12M, MACGO12M, ONSA13NE, ONSA13SW, WESTFORD, WETTZ13S, and RAEGYEB. The source exhibits a prominent relativistic jet oriented at about 270 degrees from the North Celestial Pole

Full size image

A theoretical formulation and analytical expression for the effect of source structure on the observed VLBI group delays was derived by Charlot (1990), which was applied both to simulations and observations on radio source NRAO140. This was followed by dual-frequency S/X observations of a set extragalactic radio sources to obtain single-epoch images of them. The selected sources came from a catalogue 540 sources for which positions were determined by Johnston et al. (1995). The results of the imaging were reported in three parts in Fey et al. (1996); Fey and Charlot (1997, 2000) for a total of 389 sources. This work also led to the definition of the so-called Structure Index (SI), which can be used as a measure of astrometric quality of the sources. The effects of source structure on geodetic parameters were investigated in Shabala et al. (2015) using simulated CONT11 observations with source catalogues of simulated and real quasars of various structure indices. One of their main findings was that source structure can affect the station positions on a millimetre level. They also demonstrated that as SI is defined for each source using all Earth-bound baselines, it can differ from an observed delay index on a single baseline, which quantifies the actual source structure effect on the group delay. Thus, it is also important to consider the relative orientations of the source structure and the baseline. The relative jet-to-baseline orientation and its effect on the celestial reference frame were studied in Plank et al. (2015), which used schedules from IVS observing program to simulate observations with source structure components determined using two-component source models. The model defines the source by its main component, a second component with its relative brightness w.r.t. the first, and the separation of the two. A nominal SI and median delay based on all Earth-bound baselines are determined for each source, which are compared to the actual median delay and delay index determined from the simulated observations. Since typically the observed VLBI networks do not cover the whole globe, the observed values generally are smaller than the nominal ones. Their results also clearly demonstrate that the structure delay varies with the alignment of the baseline to the jet direction, yielding higher structure delays when the two are parallel. This is also evident in the position offset estimates of the sources, where the overall trend and magnitude of the offsets w.r.t. jet alignment also depend on the SI and the relative brightness of the second component. This leads to the apparent shift of the source positions being mostly along the jet direction. Source structure effects have also been investigated using actual observations of radio sources (e.g. CONT14 campaign) (Anderson and Xu 2018; Xu et al. 2016, 2017, 2021a). These studies show that source structure leads to systematic errors in the observed delays and this effect is significant for geodetic VLBI for both legacy S/X and VGOS observations. The contribution from source structure was found to be at the level of 20 ps in both legacy S/X observations and VGOS observations. (Anderson and Xu 2018; Xu et al. 2021a). In another study by Sovers et al. (2002) based on 10 Research and Development VLBI (RDV) sessions, extended source structure effects contributed 8–30 ps to the residual weighted root mean square (WRMS) delay. It was found that for sources with extended structure on X-band modelling the source structure improved the results from the VLBI analysis.

There have also been efforts to model source structure by multiple point-like source structure models to compute corrections to the group delays by prior the analysis stage in VGOS broadband observations (Bolotin et al. 2019). The model was applied to five VGOS CONT17 sessions, in which the source 0552 + 398 was found to have abnormal post-fit residuals during the analysis stage. By applying the source structure correction model, the weighted post-fit residuals for the source decreased from approximately 14 to 3 ps.

In this paper, we investigate mitigating the source structure effect in geodetic VLBI analysis by re-weighting the group delay observables at the analysis stage in Vienna VLBI Software (VieVS; Böhm et al. 2018). We implement a weighting scheme based on the relative angles of the jet and telescope baselines as well as closure delays derived from the same observations. The VLBI data come from the sessions observed during the CONT17 observing campaign  (Behrend et al. 2020). During the campaign, there were both independent legacy S/X and VGOS networks observing. In our study, we choose to focus solely the legacy S/X sessions. There are a few key points behind this choice. Even though the relative contribution of the source structure effect w.r.t. measurement noise is expected to be larger in the VGOS observations, we still expect to see a significant effect also for S/X observations. Given that the CONT17 VGOS network is considerably smaller (6 stations in VGOS vs 14 in S/X) and concentrated on the Northern hemisphere, we have better source coverage and more robust geometry with the S/X network. Furthermore, the S/X network stations have well-established a priori coordinates and have participated in operational geodetic VLBI observations for many years. Our main interest is to evaluate the effectiveness of the re-weighting scheme against standard weighting approaches (constant additive noise, elevation-dependent noise). For this purpose, the legacy S/X sessions provide a solid data set with good spatial sampling of the sky to estimate session fit and geodetic parameters.

In Sect. 2, we discuss the data used in the analysis. In Sect. 3, we describe the analysis steps and the re-weighting scheme. The performance and limitations of the re-weighting scheme are evaluated by looking into the session fit statistics, baseline repeatabilities, and estimated geodetic parameters in Sect. 4. Finally, Sect. 5 summarizes the results and discusses future work.

2 Data

The base dataset we use to test the re-weighting scheme consists of three parts: (1) VLBI databases, (2) jet position angles (PAs) for the observed sources, and (3) root-mean-square (RMS) closure delays for the observed sources.

The VLBI databases (version 4) include the CONT17 S/X sessions observed on the Legacy-1 network. The data are openly accessible (upon registration) at the Crustal Dynamics Data Information System (CDDIS) data centre (Noll 2010) (https://cddis.nasa.gov/archive/vlbi/ivsdata/db/). The sessions were observed from the 28th of November to the 12th of December in 2017. From this time period, the total of 15 24-h sessions were observed and correlated. The observing network consists of 14 stations. The participating stations and the network geometry are illustrated in Fig. 2.

Fig. 2
figure 2

CONT17 Legacy-1 observation network

Full size image

A total of 91 radio sources were observed during CONT17. The number of observations per source as they are distributed in the sky is shown in Fig. 3. As discussed in Sect. 1, most sources exhibit jet-like structures. An approximation of this structure can be expressed as the direction of the jet as seen on the sky plane. This is given by a jet PA measured from the North.

We obtained the jet PAs for the CONT17 sources from the dataset by Plavin et al. (2022b), which is available at Plavin et al. (2022a). The database contains jet directions for in total of 9220 AGNs determined from VLBI observations on frequencies ranging from 1.4 to 86 GHz. For some sources, there are observations on several frequency bands. The database contains both frequency-averaged and individual frequency band jet directions. We cross-checked the dataset with the 91 CONT17 sources observed at 8 GHz and were able to retrieve in total X-Band jet PAs for 87 sources. For four CONT17 sources, jet PA was not available in the dataset. The process by which the AGN jet directions are determined is covered extensively in Plavin et al. (2022b). In summary, the jet directions are determined by an automated method from calibrated interferometric visibility data. This is done by model-fitting Gaussian components using a Bayesian nested-sampling algorithm. The visibility data are obtained from the AstroGeo VLBI image database.Footnote 1 The jet directions are determined from observations made on one or more epochs between 1994 and 2021 at multiple frequencies. If the source has been observed on multiple epochs, the jet direction reported in the database is the median of the individual observations. The model-fitting produces formal uncertainties for the jet PAs, which do not include model assumptions or calibration, and are thus underestimated. Additionally, jet PA uncertainties are derived from either as an average standard deviation on the band (number of epochs <5) or intraband standard deviation (number of epochs >5). The latter uncertainties are provided in the database for all sources for frequencies below 86 GHz. For the 87 CONT17 sources used in this study the jet PA uncertainties range from 1\(^{\circ }\)–64\(^{\circ }\), with a mean and median of 12\(^{\circ }\) and 8\(^{\circ }\), respectively. Time-variation of the jet PAs is relatively common in blazars; the typical circular standard deviation of the jet PA is 10\(^\circ \) over 12–16 years, but the PA variation range can be up to 150\(^\circ \) in extreme cases (Lister et al. 2013). It is important to acknowledge that the jet PAs in Plavin et al. (2022a) represent either a single epoch or a median direction in time, the jet PA estimates do not necessarily coincide temporally with the time period of CONT17 (2017). Thus, even an accurately determined jet PA may in some cases differ from the true jet direction at the time of CONT17. However, the standard deviations derived from multi-epoch observations also reflect possible real time variability of the sources. Even though the jet PA uncertainties are not included in the re-weighting, they are used to flag sources in the analysis of the source-wise residuals (see Sect. 4.2) in order to identify cases where the used jet PA might differ from the one on the observation epoch of CONT17. The jet PA sky distribution is illustrated in Fig. 4. Statistics on the jet PA uncertainties and number of observed epochs for the 87 sources are given in Table 1.

Table 1 Statistics for 87 CONT17 sources with jet PA available in Plavin et al. (2022a)
Full size table
Fig. 3
figure 3

Number of observations per source in the CONT17 sessions distributed on the sky. Sources marked with blue circles have jet PA data and orange circles have no jet PA info available

Full size image
Fig. 4
figure 4

Jet PA distribution on the sky for the CONT17 sources. Orange circles indicate sources with no jet PA info available

Full size image

In order to get an initial estimate of the magnitude of the source structure effect, we determined RMS closure delays for all 91 sources. Closure delay is the sum of the three group delay observables around a loop of a triangle, and thus it cancels exactly the station-based errors such as variation in clocks, atmospheric effects, and inaccurate station positions. Because source structure causes baseline-based errors in the observables manifesting as closure delays, it has been used to quantify the magnitude of the effect of source structure in geodetic VLBI (see, e.g. Xu et al. 2017, 2021a). We assume in this study that source structure does not change significantly during the CONT17; therefore, we used all the observations to calculate the RMS closure delays in order to obtain these statistics reliably. Uniform weighting was used in calculating the RMS of closure delays. The number of closure delays available/used per derived RMS closure value per source varies from 2 to 11,040 with a median of 1368 closure delays. The histogram distribution of used closure delays per source is shown in Fig. 5. The RMS closure delay values are between 4.57 and 77.73 ps with a mean of 31.07 ps and a median of 27.18 ps.

Fig. 5
figure 5

Histogram of number of closure delays per source that were used to calculate the RMS value

Full size image

The KASHIM11 station did not have a signal at the last four channels at X-band, and they were flagged out during correlation. For this reason, there were offsets in the corresponding closure delays, and thus, the baselines with the station KASHIM11 were excluded in deriving RMS closure delays. In order to target the effect of re-weighting on observations where we have the full set of available information (jet PA, closure delay) we also exclude the KASHIM11 in the subsequent analysis of the CONT17 sessions. The sky distribution of the RMS closure delay values is shown in Fig. 6.

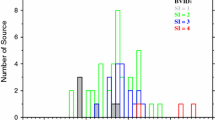
Additionally, we compared how closure delays agree as a measure for source structure with the well-known source structure measure Structure Index (SI) (Fey et al. 2009). The index divides sources into four discrete categories based on median values of calculated structure corrections to the delay. SI is used to filter and identify the most compact sources, which are selected as defining sources in the International Celestial Reference Frame (latest realization ICRF3; Charlot et al. 2020).

Fig. 6
figure 6

RMS closure delay values distribution on the sky for the CONT17 sources

Full size image

We obtained all available SI on X-band from the years 2017 and 2018 for a total of 49 CONT17 sources the from the Bordeaux VLBI Image Database (BVID) (Collioud and Charlot 2019).Footnote 2 Then within these SI performed a search with a 100-day window using the midpoint of CONT17 (2017-12-07) as the pivot date. For each source, we selected the SI that was closest in time to the pivot and within the search window. With this method, we end up with 20 sources, for which we computed the correlation coefficient between SI and RMS closure delay to be 0.85. This further indicates that closure delays are a viable method to describe source structure. The SI plotted against RMS closure delay for the 20 sources is shown in Fig. 7. Furthermore, as we move the pivot date further from CONT17 (i.e. the epoch of the RMS closure delay determination) the correlation coefficient decreases, which highlights the importance of having information on the source structure that is close in time to, e.g. geodetic observations that it is applied to.

3 Methods and analysis

The analysis of the CONT17 VLBI databases was done using VieVS.Footnote 3 For this study, we did two main modifications to the software: (1) included an option to add source structure-based noise to the weights of the observations and (2) modified the least-squares module to iteratively re-scale the additional noise so that the main solution has a (reduced) \(\chi _{\nu }^2 \approx 1\) (with a cutoff threshold of 0.01 deviation from unity). Our analysis approach was to process the databases separately in two batches: first, using only the standard weighting options available in VieVS, namely constant additive and elevation-dependent noise; secondly, adding weighting based on the RMS closure delays and relative orientation between the jet angle and the uv-baseline of the observation. The uv-baseline is the baseline given in u and v coordinates on a uv-plane, which is a plane perpendicular to the source direction vector, as seen from the baseline, with u increasing to the left (as seen towards the source) and v pointing northward. Before doing the main analysis of the two batches, the databases were processed to remove any clock breaks and to detect other problems in, e.g. cable delay calibration data.

Fig. 7
figure 7

Correlation between SI on X-band and RMS closure delay for 20 CONT17 sources that have an SI value available in BVID (Collioud and Charlot 2019) within a 100-day search window from the midpoint of CONT17 (2017-12-07). If multiple SI were found for a source, the closest one to the pivot was selected

Full size image

3.1 Re-weighting scheme

The formal errors for the group delays coming from the correlation and fringe fitting process, denoted here by \(\sigma _\textrm{corr}\), are read from the analysed VLBI databases. They form the basis of the stochastic model used in the least-squares estimation. Typically, these errors tend to be too optimistic. Thus, in routine geodetic VLBI analysis, the errors are inflated in some way so that the solution has \(\chi _\nu ^2\) close to unity. These inflated errors aim to take into account unexplained errors due to measurement noise, wet troposphere, and other error sources including the effect of the source structure. In standard VieVS, the noise inflation can be done by either adding a constant additive noise to the formal error of each observation or elevation-dependent noise. The latter option suggests that the unexplained variation in the group delay residuals is merely due to atmospheric effects. The constant term can be adjusted freely (default magnitude 5 mm), and the elevation-dependent noise is set to 6 ps scaled by the sine of elevation per station (Gipson et al. 2008). The weight matrix \(P_\textrm{obs}\) used in the least-squares estimation can be written as:

$$\begin{aligned} P_{\text {obs}} = \begin{bmatrix} \dfrac{1}{\sigma _{{\text {obs,1}}}^2} &{} 0 &{} 0 &{} \cdots &{} 0\\ 0 &{} \dfrac{1}{\sigma _{\text {obs,2}}^2} &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} \dfrac{1}{\sigma _{\text {obs,3}}^2} &{} \cdots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{1}{\sigma _{\text {obs,i}}^2} \\ \end{bmatrix}, \end{aligned}$$
(1)

where \(\sigma _\textrm{obs,i}\) is the standard deviation used for the ith observation. The \(\sigma _\textrm{obs,i}\) is a composite that includes various error contributions depending on the selected weighting methods.

In this study, we derive an additional source structure-dependent noise term, \(\sigma _{\text {source}}\). The sensitivity (in terms of an additional delay component to the group delay) of an observing baseline to a non-point-like source with a jet-like structure can be characterized by their relative orientations. The baseline coordinates are in the Earth-fixed Cartesian system, and the jet PA is expressed w.r.t. its relative right ascension and declination. To compute the relative orientation, these need to be expressed in the same coordinate system. The baseline vector is transformed to u, v coordinates, and the jet PA can be directly expressed in the same uv-plane. The jet PA is read from the North Celestial Pole, increasing to the counterclockwise direction. The relative angle, \(\theta _{\textrm{rel}}\), is thus the angle between the jet PA and baseline vector in the uv-plane. As we are interested in how the fringe pattern of the baseline aligns with the jet PA, we need only to consider the smaller (\(\min \left\{ \theta _{\textrm{rel}},180^{\circ }-\theta _{\textrm{rel}}\right\} \Rightarrow \theta _{\textrm{rel}} \in \left[ 0^{\circ },90^{\circ } \right] \)) of the two possible angles. When the jet is perfectly aligned with the baseline in the uv-plane (\(\theta _{\textrm{rel}}\)), we expect to see the largest effect from the source structure. Combining the information on the relative angle and the RMS closure delay of the source, the source structure noise-dependent term is given by:

$$\begin{aligned} \sigma _{\text {source}} = \frac{\pi }{2} \times \tau _\text {c} \times \cos (\theta _{\text {rel}}), \end{aligned}$$
(2)

where \(\tau _\textrm{c}\) is the RMS closure delay of the observed source and \(\theta _{\text {rel}}\) is the relative jet-uv-baseline angle. The expression is scaled by a factor of \(\tfrac{\pi }{2}\) so that when averaged over all the relative angles, the noise term \(\sigma _{\text {source}}\) averages to \(\tau _\text {c}\). The scaling assumes that the relative angles are uniformly distributed between \(0^{\circ }\) and 90\(^{\circ }\).

From this equation, we can see that if the relative angle between the jet and the uv-baseline is exactly 90\(^\circ \) the cosine term equals 0 and there is no noise contribution from the source structure term. This effect is visualized very well in the quasar source structure simulation study by Shabala et al. (2015).

For 96% sources (see Table 1), there is jet angle information available. For the sources that we have no information available the relative angle is set to 45\(^\circ \). The reasoning of this choice is to account for the situation where there might be a jet present but as there is no orientation information, we set the expected contribution to the mean value.

Table 2 Expressions of \(\sigma _\textrm{obs}\) for the different weighting methods (constant, const; elevation, elev; source structure, SS)
Full size table

Furthermore, less structure effect is expected on the shorter baselines. The radio sources observed by geodetic VLBI are all compact at pc scales and show extended structure at k-pc scales. Shorter baselines have lower angular resolutions, at which the geodetic sources appear all as compact. This has been extensively demonstrated by using 40 years of geodetic observations in Xu et al. (2019). We take this into account by scaling the noise term based on the length of the baseline in the uv-plane. Additionally, we set a cutoff threshold of 3000 km in the uv-plane, below which no source structure-dependent noise is added to the weights. This emphasizes the influence of long baselines, where we most likely have a larger source structure effect.

Thus, finally the \(\sigma _\textrm{source}\) used in the analysis is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma _{\text {source,bl}} = \sigma _{\text {source}} \times \frac{\text {BL}_{\text {uv}}}{R_\textrm{e}}, &{} \text {BL}_{\text {uv}} > 3000~\text {km} \\ \sigma _{\text {source,bl}} = 0, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$
(3)

where BL\(_\text {uv}\) is the baseline length in the uv-plane and \(R_\textrm{e}\) is the Earth radius.

In the analysis, the solution is iterated by scaling the weights by multiplicative factor k so that \(\chi _{\nu }^2 \approx 1\). This is done by scaling only the constant term. The magnitude of the source structure noise term for an observation is determined by the relative angle and the RMS closure delay. While the relative angle term varies with the baseline orientation for each observation, the RMS closure delay term for a particular source remains constant from session to session. Because the source structure term alone cannot and should not explain all the remaining noise after applying \(\sigma _\textrm{corr}\), a weighting model also needs to include a constant and/or elevation-dependent noise term to account for measurement and atmospheric noise. The elevation-dependent noise per observation is given by:

$$\begin{aligned} \sigma _{\text {ele}}^2 = \left( \frac{6~\text {ps}}{\sin (e_\text {1})}\right) ^2 + \left( \frac{6~\text {ps}}{\sin (e_\text {2})}\right) ^2, \end{aligned}$$
(4)

where \(e_1\) and \(e_2\) are the elevation angles for stations 1 and 2, and 6 ps is the initial magnitude of the elevation-dependent noise (i.e. estimated noise in the zenith). To evaluate the impact of these different components on the weighting, we analyse the data using four different weighting methods, which consist of combinations of correlator formal error, constant, elevation-dependent, and source structure-dependent noise.

Table 2 lists the k-scaled \(\sigma _{\text {obs}}^2\) for the different weighting methods, which are assigned labels W1–W4. As shown in this table, these weighting methods have different combinations of adding a constant noise (const), elevation-dependent noise (elev), and/or error contribution of source structure (SS).

We analysed all the CONT17 Legacy-1 network databases using the weighting methods described in this chapter. We aim to compare solutions one-to-one with the same set of observations that only differ in their weighting methods. Thus, we did not use an automated outlier detection and elimination in order to retain the same set of observations for all weighting methods. However, since extremely large individual outliers can have a disproportionately large effect on the results, after initial analysis the residuals were inspected session by session for all the weighting methods. We detected in total 8 observations in 7 sessions in the range of 20–100 cm, which were clearly much larger than the overall magnitude of the residuals in these sessions. Such high values cannot be attributed to be caused by source structure. However, depending on the particular baseline-to-jet orientation of these single observations, they can end up being heavily down- or upweighted in the source structure-dependent weightings (W3, W4) when compared to the reference solutions (W1, W2). In these cases, comparing the session fits and the WRMS of the residuals for the observed sources between W1, W3 and W2, W4 are unfeasibly skewed. For example, in the most extreme case of the 100 cm residual, suppressing the observation led to 2 mm change in the difference between session fit WRMS of W2 and W4, with the pre-elimination WRMS values being approximately 10.7 mm (W4), 13.1 mm (W2) and the new 9.7 mm (W4), 10.1 mm (W2). Thus, these 8 observations were manually flagged as outliers and removed from the final analysis. As they are removed completely from the processing, the set of used observations between the weightings remains identical.

When the stochastic model is constructed using the source structure-dependent weighting (W3 and W4), the variables are the relative angle and the RMS closure delays. For individual sources, the source-dependent factors (jet angle, RMS closure delay) remain fixed for from session to session. The relative angles depend on the geometry of the individual observations. The distribution of the relative angles over the 15 sessions is shown in Fig. 8. From the distribution, we can see that, when the relative angles are pooled for all sources and sessions, the whole angle space from 0\(^{\circ }\) to 90\(^{\circ }\) is well-sampled. There are no visible biases, the orange bar shows the contribution from the forced relative angle of 45\(^\circ \) for sources with no jet PA available.

Fig. 8
figure 8

Number of observations per relative jet angles in the 15 CONT17 sessions. The orange bar in the distribution corresponds to cases where no jet angle info was available and the relative jet angle was set to 45\(^\circ \)

Full size image

4 Results

The results from the analysis CONT17 with the different weighting approaches described in the previous section were evaluated in terms of session fit statistics and estimates of geodetic parameters, namely station positions, baseline length repeatability, and EOPs. Furthermore, we investigated the influence of session- and source-dependent parameters (e.g. RMS closure, number of observations) on the source-wise delay residuals.

We compare the results from the analysis using the weighting methods W1 and W2 as reference data and compare them to the source structure-dependent W3 and W4, respectively (see Table 2).

In order to assess the possible effect of omitting a statistical outlier elimination in the analysis, we performed a rough outlier detection and elimination test for both weightings W2 and W4. The 8 manually detected outliers were already eliminated prior to these tests. We focus on testing for large (5\(\sigma \)) outliers, since they could have a disproportionately large effect in the results. The outlier test and elimination were done sequentially by detecting and removing the marked observations in repeated analyses.

The \(\chi ^2\) iteration was not applied during these outlier runs, so the amount of constant noise is fixed to its initial 2 mm value for both weightings. After the first run, the total number of detected outliers in the 15 sessions was 230 (W2) and 412 (W4). The outliers were then eliminated iteratively until none were detected. The final number of outliers was 291 (W2) and 526 (W4), which quantitatively represent a small fraction of the total number of observations (nearly 130,000) for CONT17.

The sessions were re-analysed with the detected outliers removed. In terms of the session fits and geodetic parameter estimates, the results were in general similar to the ones carried out without outlier removal. Hence, as discussed earlier, to keep the analysis process otherwise as identical as possible between the weighting strategies, we only include here the results from the main analysis run without outlier detection.

4.1 Session fit statistics

The session fit statistics are presented in terms of WRMS values. As discussed in 3.1 due to the iterative adjustment of the noise terms the \(\chi _{\nu }^2\) is for all sessions within 0.01 of unity. From session to session, the WRMS values are within the range of 8–12 mm. The mean WRMS reduction percentage by using source structure-dependent noise is approximately 6.0% for W1 vs. W3 and 4.9% for W2 vs. W4. The mean and median WRMS values over the whole CONT17 for the different weighting methods are listed in Table 3. When averaging over all of the 15 session-wise WRMS values, we see a very small but consistent improvement when using the source structure-based weighting. When the results are investigated session per session, we notice larger variations in the improvement. The WRMS comparison and improvement ratios when using k-scaled (see, e.g. Table 2) constant (W1, W3) or k-scaled constant and elevation-dependent noise (W2, W4) with and without source structure-dependent noise are shown in Figs. 9 and 10. When the source structure-dependent weighting is compared to the respective reference solutions session-wise, we see that the improvement is consistent throughout the CONT17. The inclusion of elevation-dependent noise slightly reduces the overall WRMS compared to only using constant noise. For both cases, the addition of source structure-dependent noise reduces the WRMS for all sessions. The relative improvement in the residuals using the source structure-dependent noise is slightly smaller when elevation-dependent noise is included in the weighting. Overall the best weighting method in terms of mean WRMS includes both elevation- and source structure-dependent noise (W4). The inclusion of elevation-dependent noise should provide a more realistic error model for the observations. Thus, for the source-wise residuals (see Sect. 4.2 and geodetic parameter estimates (see 4.3) investigation we focus on W2, W4, and their difference.

Table 3 Mean session fit WRMS over 15 CONT17 sessions for the different weighting methods (constant, const; elevation, elev; source structure, SS)
Full size table

For each observation, these two noise terms along with the formal errors from the correlation are fully determined prior to \(\chi _{\nu }^2\) iteration. Thus, the k-scaled constant term accounts for all the remaining unexplained variance in the observations. The magnitude of the k-scaled constant term gives a measure of how much additional noise is needed for the stochastic model to explain the variation in the residuals. Figures 11 and 12 show the contribution from the constant term for the two reference solutions (W1, W3) and the respective solutions with source structure-dependent noise. The \(\sigma _\textrm{corr}\) values from the fringe-fitting depend only on the observations and are identical for all weighting methods. They range from 4.4 to 5.5 mm with a mean of 5.0 mm. The noise contributions for the weighting methods are listed in Table 4. For each session, average noise magnitudes are computed for the terms contributing to the weightings methods. The table columns show the minimum, maximum, and pooled average from the 15 CONT17 sessions. From the table, we see that in order to get \(\chi _{\nu }^2 \sim 1\) we need to add a large amount of constant noise in all four weighting cases. In W1 and W2, the constant term is dominant in the overall noise profile. In W3 and W4, the magnitude of the source dependent-noise is on average below the contribution from the noise from fringe-fitting. When elevation-dependent terms are included in the noise model in W2, the contribution from the constant term is reduced as expected. In W4, when compared to the other three weightings, the constant term is reduced and has on average similar magnitude than \(\sigma _{\textrm{corr}}\), \(\sigma _{\textrm{ele}}\), and \(\sigma _{\textrm{source,bl}}\), but with higher peak-to-peak variation (2.3–8.0 mm). In both W3 and W4, the contribution from the source-dependent noise has on average the lowest magnitude out of the noise terms.

Fig. 9
figure 9

Session-wise WRMS using k-scaled constant additive noise without source structure-dependent noise (W1) and with source structure-dependent noise (W3). The solutions are iterated until \(\chi _{\nu }^2 \sim 1\) for the residuals. Shown are the session fit WRMS value for each session (left) and the ratio of these WRMS values for W3/W1 as well as the percentage of improvement in (i.e. reduced) WRMS for W3 w.r.t. W1 (right)

Full size image
Fig. 10
figure 10

Session-wise WRMS using k-scaled constant additive and elevation-dependent without source structure-dependent noise (W2) and with source structure-dependent noise (W4). The solutions are iterated until \(\chi _{\nu }^2 \sim 1\) for the residuals. Shown are the session fit WRMS value for each session (left) and the ratio of these WRMS values for W4/W2 as well as the percentage of improvement in (i.e. reduced) WRMS for W4 w.r.t. W2 (right)

Full size image

In none of the four weighting approaches, the formal uncertainty from fringe fitting, elevation-dependent noise, and source structure-dependent noise combined are enough to explain all the variance in the data, and additional noise is needed to reach \(\chi _{\nu }^2 \sim 1\) for the residuals. The group delay uncertainties from fringe fitting are known to be underestimated (hence the need for additional noise). It is also possible that the magnitude of elevation- and source structure-dependent noise terms are also underestimated. In the case of elevation-dependent noise, the magnitude (6 ps in zenith) and mapping are identical for all observations, which could ignore some station-dependent effects. The scaling of the source structure-dependent noise could also be refined by, e.g. computing not just source- but also baseline-dependent RMS closure delays. In this work, the baseline-dependency accounted for the baseline length scaling, which is applied to the noise term after the RMS closure delays are already computed.

The balance and results of the different weightings are reflected in the resulting WRMS ratios (Figs. 9, 10) and the respective noise contributions in the solutions (Figs. 11, 12). The increase in session fit WRMS is highly correlated with the magnitude of the constant noise term. For example, with W1 the Pearson correlation coefficient between WRMS and \(k\sigma _{\text {const}}\) for the 15 CONT17 sessions is \(\rho _{k\sigma _{\text {const}},\text {WRMS}} = 0.91\). Similarly, for W4 the correlations are \(\rho _{k\sigma _{\text {const}},\text {WRMS}} = 0.91\), \(\rho _{\sigma _{\text {ele},\text {WRMS}}} = 0.12\), and \(\rho _{\sigma _{\text {source}},\text {WRMS}} = -0.06\).

Fig. 11
figure 11

Noise contribution of the k-scaled constant term to \(\sigma _\textrm{obs}\) in weightings W1 and W3

Full size image
Fig. 12
figure 12

Noise contribution of the k-scaled elevation term to \(\sigma _\textrm{obs}\) in weightings W2 and W4

Full size image

4.2 Source-wise residuals

In order to better understand the performance of the source-structure dependent weighting, the results were also analysed in terms of source-wise delay residuals. While the session fit statistics show slight and consistent improvement when source structure is included in the stochastic model, the effect is inherently source-based and inspecting the performance of individual sources can give clues where the weighting either succeeds or fails in improving the residuals w.r.t. the reference solution. Several factors could have an effect on the source-based residuals. The jet PAs have their own uncertainty (see Table 1). The RMS closure delays themselves are in one sense an accuracy estimate. However, the number of observations (baseline triangles) used to derive the closures (see Fig. 13) as well as the number of observations per source can vary significantly. Figure 13 illustrates the influence of closure delay RMS and the number of observations to the source-wise WRMS residuals. The WRMS value for each source is averaged over the CONT17 sessions, weighted by the number of observations per session.

Table 4 Minimum, maximum, and average noise contributions of the 15 CONT17 sessions for the weighting methods
Full size table
Fig. 13
figure 13

Source-wise residual WRMS for weightings W2, W4 (top) and their difference W2–W4 (bottom). The values are plotted against the RMS closure associated with the sources (left) and the number of observations per source (right). The WRMS value for each source is an average over the CONT17 sessions, weighted by the number of observations per session. Additionally, information on the jet angle quality is included for a set of sources. These include sources with no jet PA available (black) and jet PA uncertainty larger than 20\(^\circ \) (yellow)

Full size image

Starting from the top left plot (Fig. 13), when the residuals are plotted against the RMS closure a pattern with a positive correlation emerges for both weightings. This result implies as expected that sources with higher closure delays have a stronger source structure effect, thus leading to higher residuals. However, there is a degree of scatter present and a high closure value does not uniformly lead to worse residuals for all sources. Since this variation is present in both W2 and W4, it is not directly related to the weighting methods but is intrinsic to the observations of the sources.

Next, in the bottom left plot (Fig. 13) the differences between the WRMS of W2 and W4 are illustrated. All the residuals, where the source structure-dependent weighting performs better, are marked with green circles. The cases, where the reference solutions perform better, are marked with magenta circles. In total, W4 leads to lower residuals for 63 and W2 for 28 sources.

The differences show that for some sources there is a clear trend that the source structure-based weighting leads to better residuals with higher RMS closure magnitudes. However, similarly for some high closure sources, W4 fails to improve the residuals. For some of these sources the underperformance could be explained by inadequate jet angle information. For the two sources, where W2 outperforms W4 and the jet angle information is missing (magenta circles, black outlines) it is likely that the 45 \(^\circ \) best-effort-guess used for such sources does not coincide with the true jet angle.

Lastly, on the right-hand side (Fig. 13) the same residuals are plotted against the number of observations per source. Alternatively, the number of observations used per closure delay could be used, but these lead to nearly similar pattern as the two are highly correlated (see Fig. 14). The solution-wise residuals for W2 and W4 in the top plot show that the residuals tend to decrease when the number of observations increases. It is not directly obvious what are the main causes of this pattern. Possible explanations could be that the WRMS of the residual is less sensitive to the random scatter with a higher number of observations. Furthermore, a lower number of observations may indicate that the source is not visible to the whole network thus reducing the number of observing baselines, which could lead to the observations being more sensitive to noise in the solution. Furthermore, for a set of sources high RMS closure values correlate with the lower number of observations, making the closure determination for these sources potentially more sensitive to scatter.

From the bottom right plot, we can see that many of the high RMS closure sources, where the source structure-dependent weighting performed worse than the reference, tend to be sources with less than 1000 observations. Furthermore, nearly all of the sources where W2 outperformed W4 have less than 2000 observations. It is possible that below a certain threshold, the probability that the RMS closure delay determination does not adequately represent the magnitude of the source structure effect in terms of the source structure-based weighting, leading to degradation rather than improvement of the residuals.

The correlations between the W2, W4 and W2–W4 and a set of source-wise parameters are summarized in Fig. 14. The correlation matrix includes source-wise Pearson cross-correlations between the residual terms, the number of sessions the source is observed, RMS closure delay, and the number of observations used per closure delay. The numerical correlation values are in agreement with the visual inspection of the residual figures.

Fig. 14
figure 14

Correlation matrix for the W2, W4 residuals and parameters associated with the individual sources. These include RMS closure delay, the number of sessions the source is observed, the number of observations to the source, and the number of observations used for RMS closure delay determination

Full size image

4.3 Geodetic parameter estimation

Lastly, we investigated how the estimated geodetic parameters are influenced by the choice of different weighting methods. The sessions were analysed using the default parametrization in VieVS @. The parameters are estimated by session offsets w.r.t. a priori values or with piece-wise linear offsets (PWLO). The clocks and troposphere were parametrized by 60-min and 30-min PWLO, respectively. Station positions and EOPs were estimated as one offset per session w.r.t. a priori values from ITRF2020 (Altamimi et al. 2023) and IERS EOP C04 20.

The effect of source structure-dependent weighting to the station positions was by comparing W4 and W2 3D position residuals and formal errors for each station. The \(\mathrm {\Delta }(\text {W2}-\text {W4})_{\text {3D}}\) error bars were estimated according to error propagation by \(\sigma _{\mathrm {\Delta }}^2\) = \(\sigma _{\text {W4}}^2\) + \(\sigma _{\text {W2}}^2\). Figures 15 and 16 show the differences for station position residuals and formal errors, respectively.

Whereas the session fit statistics and residual inspection showed more consistent improvement between W4 and W2, the interpretation of the station positions is less straightforward. For some stations, the residuals and formal errors are improved and for some, they are degraded. This may be caused partly by the network geometry and No-Net-Translation/No-Net-Rotation constraints used in the analysis. Moreover, the improvement seen in terms of WRMS residuals has a relatively small magnitude. Thus, the geodetic parameter estimates could be partly corrupted by other unaccounted systematic and non-systematic errors. All the residual differences in Fig. 15 are within \(\sigma _{\text {3D}}\) from 0. The same small magnitude of the change in station position residuals is also evident from the baseline repeatability plot illustrated in Fig. 17. We define the baseline length repeatability as the WRMS of the scatter of the baseline length residuals about their weighted mean. We can note that the scatter in the repeatability from baseline to baseline over the baseline length span is quite high for the longer baselines. This scatter can be partially attributed to the fact that we do not include any statistical outlier elimination in the analysis.

Fig. 15
figure 15

Station position residual differences between W2 and W4 for the 15 CONT17 sessions. The blue diamonds show the difference of 3D offset w.r.t. ITRF2020 a priori for each station between W2 and W4. The error bars show the 3D formal error of the offsets. Reported above each time series is the weighted mean of the offsets computed using the respective offsets and formal errors

Full size image
Fig. 16
figure 16

Station position formal error differences between W2 and W4 for the 15 CONT17 sessions. The red diamonds show the difference of 3D offset w.r.t. ITRF2020 a priori formal errors for each station between W2 and W4. Reported above each time series is the mean of the formal errors

Full size image

For all sessions, a full set of EOPs (UT1–UTC, polar motion, precession/nutation) were estimated as one offset per session w.r.t IERS EOP C04. In terms of mean WRMS over the 15 sessions, the results follow a similar pattern that was seen with the station positions; for some parameters, we see an improvement and for some, the estimates degrade. However, for most of the sessions the changes are very small and fall within the formal errors of the two weighting methods. The variations in the EOP residuals of the individual weighting solutions from session to session are considerably larger than the differences between the weighting methods. Figure 18 shows the EOP residuals along with their formal errors. The session-wise differences W2–W4 for the absolute value of the EOP offsets and formal errors, along with their mean, median, and standard deviations of all sessions, are listed in Table 5. Given the order of calculation (W2–W4), positive values correspond to smaller EOP residuals for W4 compared to W2. On average we get slightly larger offsets for all EOP with W4. We see that the differences in the EOP estimates and formal errors overall do not have a consistent pattern in the sense that one weighting method would perform better in both for all EOPs and sessions. The differences between the offsets vary from positive to negative from session to session for all EOPs. For the polar motion and nutation parameters, the variability is quite large, as can be seen by the comparison of the mean and median to the standard deviations of the respective differences.

With the formal errors, a more consistent pattern emerges. For all the EOPs, in nearly all sessions, the differences are negative, i.e. W4 results in larger formal errors than W2. The variations in the differences are moderate from session to session, which is reflected in the standard deviations. The magnitude of the differences of the formal errors tend to be on the same order of magnitude as the differences in the respective offsets. An exception to the aforementioned is \(\sigma _{dX}\), which has a comparably large and consistent bias of approximately −34 \(\upmu \)as between W2 and W4 for all 15 sessions. The dX pole offset also has the highest variability in the differences of the offset estimates.

The reason for the patterns seen in the EOP offsets and formal errors in the comparison of W2 and W4 are not immediately evident. However, a simulation study by Shabala et al. (2015) showed that source structure can cause repeatable incorrect measurements of EOP. Thus, downweighting the observations by source structure may lead to more accurate but less precise parameter estimates. In particular, it is unclear why the \(\sigma _{obs}\) used in the W4 weighting scheme seem to especially propagate into dX uncertainties, consistently inflating them compared to W2. These issues require further investigation in future work.

Fig. 17
figure 17

Baseline repeatability with and without source-structure-dependent noise using k-scaled constant and elevation-dependent noise. The shaded regions are \(\pm 1\sigma \)-intervals of the respective quadratic fits

Full size image
Fig. 18
figure 18

EOP residuals and formal errors for the 15 CONT17 sessions analysed with W2 and W4

Full size image
Table 5 Session-wise differences of absolute values of EOP offset estimates and formal errors for W2–W4 estimated from CONT17 sessions
Full size table

5 Summary and future work

We extended the VieVS analysis software with the capability to add source structure-dependent noise terms into the stochastic model of the least-squares estimation process. The source structure was parametrized by two components: RMS closure delay and relative orientation of the direction angle of the relativistic jet and the uv-baseline orientation. Using this augmented weighting method, we analysed the CONT17 Legacy-1 network sessions. The comparison analysis was done by generating reference solutions, which use the same observations and noise components for the weighting excluding the source structure component. The RMS closure delays were derived from the same CONT17 observations. The jet PAs were obtained from the AGN jet direction database Plavin et al. (2022a).

Our analysis reveals that including the source structure-dependent component on average improves the session fit statistics slightly. The degree of improvement is quite stable, but there is still some variation from session to session. On average the session fit WRMS reduced by approximately 4.9% (W4 w.r.t. W2), but there are considerable variations from session to session. Source-wise residual inspection shows that the most important predictors for the good or bad performance of the source structure-dependent weighting seem to be a combination of the magnitude RMS closure delay as well the number of observations per source. However, for geodetic parameters we do not see any statistically significant improvement (or degradation). We investigated how the weighting affects the station position estimates (offsets w.r.t. a priori and baseline length repeatability) and EOPs. We find that station positions offsets vary from session to session during CONT17 with no statistically significant biases for any of the stations. The variation in the 3D offset estimate difference of W2 and W4 all include zero within the estimated error bars. For the formal errors of the station position offset estimates W4 weighting leads to higher averaged values for some stations, but nonetheless the average differences between W2 and W4 are all below 1 mm. This is also reflected in the baseline repeatabilities, which overlap within a \(\pm \sigma \)-interval. The variation in EOP estimates from session to session is much higher than any differences between the estimates from W2 and W4. For all sessions the EOP estimate differences are within the formal errors from one another. In some cases, such as \(\sigma _{dX}\), the formal errors are consistently larger with W4 w.r.t W2. This could be due to some network effects of CONT17. The seemingly small effect, but at times very consistent effect, on geodetic parameters needs further investigation. It could be beneficial to include more sessions into the analysis or focus on a narrower set of parameters. One testbed for such analysis could be the IVS Intensive sessions.

Furthermore, for any particular source the accuracy of the used jet angle could influence the performance. The jet PA used in the analysis represents the jet direction as a single value. In case of multiple epochs, the direction is given by the median of single values at particular epochs. Thus, the used value may not accurately represent the true direction at the time of CONT17. One way to control this would be to obtain newer reference images and evaluate the impact of any changes in the angles. Furthermore, including higher frequencies into the jet PA estimation could be investigated, since longer baselines are more sensitive to the part of the jet closer to the core of the AGN.

On the other hand, the weighting method implemented here is relatively simple since it essentially considers the sources as objects with a bright core and a jet. Nevertheless, even with this simplified approach and S/X data, we do see a consistent improvement in terms of delay residuals when the source structure is accounted for in the stochastic model. The inspection of source-wise residuals also shows that there are clearly sources where the weighting works extremely well, and for some sources the effect is the opposite. This warrants further investigation in determining source-based predictors that could indicate whether the weighting is likely to be advantageous. This will most likely require that the weighting scheme is refined to account for more parameters, such as the size of the jet.

Table 6 CONT17 sources and their structure-related properties
Full size table

Here we still focused on the S/X data. The next logical step is to apply the weighting method developed here for VGOS data. With VGOS we expect that the reduced measurement noise will make the source structure-related systematic errors larger. Thus it is important to find ways to mitigate these effects in order to reach the 1-mm accuracy goal. An alternative, and in some sense preferable, way to deal with source structure would be to model or observe it a priori or simultaneously during the geodetic observations. The advantage of the approach presented here is that it is very simple to implement once the required parameters are predetermined. As the weighting relies on these source-based parameters, it would be beneficial to derive a sensitivity model that could gauge and adjust the weights based on our level of confidence in these source parameters. The results of this study may also suggest that in order to handle the effects of source structure, a purely weighting-based approach is not adequate, but modelling the effect as shown by Xu et al. (2021b) is required. This, along with applying the weighting scheme for VGOS is left for future work.